Bedna na nakloněné rovině
Úloha číslo: 97
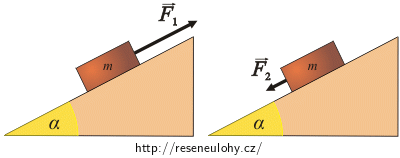
Bednu je možné posouvat rovnoměrným pohybem nahoru po nakloněné rovině silou o velikosti F1, dolů po nakloněné rovině silou o velikosti F2. Určete koeficient smykového tření f mezi bednou a nakloněnou rovinou, platí-li F1 = 6F2 a obě síly jsou rovnoběžné s nakloněnou rovinou, která svírá s vodorovnou rovinou úhel α = 15°.
Zápis
m hmotnost bedny α = 15° sklon roviny F2 velikost síly potřebné pro rovnoměrný pohyb bedny dolů po nakloněné rovině F1 = 6F2 velikost síly potřebné pro rovnoměrný pohyb bedny nahoru po nakloněné rovině f = ? koeficient tření mezi bloky a rovinou Nápověda 1 – síly působící na bednu, pohybové rovnice
Nakreslete si obrázek a vyznačte do něho všechny síly působící na bednu:
1) Bednu posouváme silou F1 směrem nahoru.
2) Bednu posouváme silou F2 směrem dolů.
Napište pohybovou rovnici pro každý z těchto případů.
Nápověda 2 – třecí síla, výpočet koeficientu tření
Uvědomte si, na čem závisí třecí síla a jak se dá vyjádřit. Vztah pro třecí sílu pak dosaďte do pohybových rovnic (1) a (3). Získáte 2 rovnice se dvěma neznámými. Spočtěte z nich koeficient tření.
CELKOVÉ ŘEŠENÍ
Do obrázku vyznačíme všechny síly působící na bednu v obou případech a napíšeme pro ni pohybové rovnice.
Síly působící na bednu:
Na bednu v obou případech působí tyto síly:
\(\vec{F}_\mathrm{G}\)…síla tíhová
\(\vec{F}_1(\vec{F}_2)\)…síla, kterou tlačíme bednu
\(\vec{N}\)…síla, kterou tlačí podložka
\(\vec{F}_\mathrm{t}\)…síla třecí
Orientace sil je patrná z obrázků.
Pohyb nahoru:
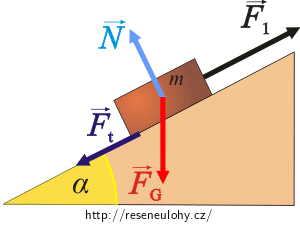
Pohyb dolů:
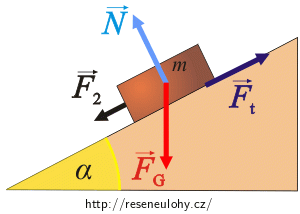
Pohybové rovnice:
Pohybová rovnice pro pohyb bedny do kopce:
\[\vec{F}_\mathrm{G}+\vec{N}+\vec{F}_1+\vec{F}_\mathrm{t}\,=\,m\vec{a}_1\,=\,0\,.\]Pohybová rovnice pro pohyb bedny z kopce:
\[\vec{F}_\mathrm{G}+\vec{N}+\vec{F}_2+\vec{F}_\mathrm{t}\,=\,m\vec{a}_2\,=\,0\,.\]Oba pohyby jsou rovnoměrné přímočaré, zrychlení bedny je v obou případech nulové.
Pohybové rovnice přepíšeme skalárně:
Soustavu souřadnic volíme tak, že osu x orientujeme ve směru pohybu bedny. Osa y je kolmá na osu x.
Sílu \(F_\mathrm{G}\) rozložíme na 2 složky do směru těchto os:
\[F_\mathrm{{G}_x}\,=\,F_\mathrm{G}\sin\alpha,\] \[F_\mathrm{{G}_y}\,=\,F_\mathrm{G}\cos\alpha.\]Pohyb bedny nahoru:
\[x:\qquad -F_\mathrm{G}\sin\alpha+F_1-F_\mathrm{t}\,=\,0,\tag{1}\] \[y:\qquad N-F_\mathrm{G}\cos\alpha\,=\,0.\tag{2}\]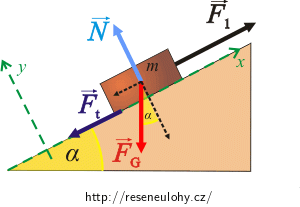
Pohyb bedny dolů:
\[x:\qquad F_\mathrm{G}\sin\alpha+F_2-F_\mathrm{t}\,=\,0,\tag{3}\] \[y:\qquad N-F_\mathrm{G}\cos\alpha\,=\,0.\tag{4}\]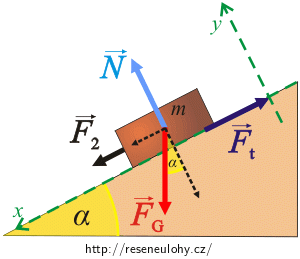
Třecí síla:
Třecí síla působící na bednu je úměrná tlakové síle, kterou bedna působí na nakloněnou rovinu. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí nakloněná rovina na bednu. Zapíšeme to rovnicí:
\[F_\mathrm{t}\,=\,fN\,.\]Sílu N vyjádříme z rovnice (2):
\[N\,=\,F_\mathrm{G}\cos\alpha\,. \]Pro třecí sílu platí:
\[F_\mathrm{t}\,=\,fF_\mathrm{G}\cos\alpha\,.\]Výpočet koeficientu tření:
Dosadíme do pohybových rovnic (1) a (3) vztah pro třecí sílu. Sílu F1 vyjádříme jako 6F2:
\[-F_\mathrm{G}\sin\alpha+6F_2-F_\mathrm{G}f\cos\alpha\,=\,0,\tag{5}\] \[F_\mathrm{G}\sin\alpha+F_2-F_\mathrm{G}f\cos\alpha\,=\,0.\tag{6}\]Rovnici (6) vynásobíme šesti a odečteme od ní rovnici (5):
\[-F_\mathrm{G}\sin\alpha+6F_2-F_\mathrm{G}f\cos\alpha\,=\,0,\] \[6F_\mathrm{G}\sin\alpha+6F_2-6F_\mathrm{G}f\cos\alpha\,=\,0,\]
\[7F_\mathrm{G}\sin\alpha-5F_\mathrm{G}f\cos\alpha\,=\,0,\] \[7F_\mathrm{G}\sin\alpha\,=\,5F_\mathrm{G}f\cos\alpha\hspace{20px}|:(5F_G\cos\alpha),\] \[f\,=\,\frac{7}{5}\mathrm{tg}\alpha.\tag{7}\]Dosadíme do vztahu (7) číselně:
\[f\,=\,\frac{7}{5}\,\mathrm{tg}15^{\circ}\,\dot=\,\frac{7}{5}\,\cdot0{,}268\,\dot=\,0{,}38.\]CELKOVÁ ODPOVĚĎ
Koeficient smykového tření mezi bednou a nakloněnou rovinou je \[f\,=\,\frac{7}{5}\mathrm{tg}\alpha\,\dot=\,0{,}38.\]





