Kostky spoutané vlákny
Úloha číslo: 141
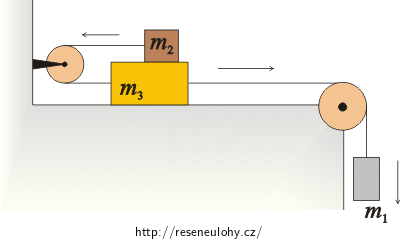
Trojice kostek o hmotnostech m1, m2 a m3 je vzájemně spoutána vlákny, jak ukazuje obrázek. Součinitel smykového tření je mezi všemi styčnými plochami stejný a má hodnotu f. Určete zrychlení kostek a tahovou sílu napínající obě vlákna. Hmotnost obou kladek ani vlákna neuvažujte.
Zápis
m1 hmotnost první kostky m2 hmotnost druhé kostky m3 hmotnost třetí kostky f součinitel smykového tření mezi libovolnými dvěma plochami a = ? velikost zrychlení kostek T1 = ? velikost tahové síly napínající vlákno mezi kostkami m2 a m3 T2 = ? velikost tahové síly napínající vlákno mezi kostkami m3 a m1 Nápověda 1– síly působící na jednotlivé kostky, pohybové rovnice
Uvědomte si, jaké síly působí na jednotlivé kostky, a napište pro každou z nich pohybovou rovnici.
Doporučení: Pro přehlednost si nakreslete pro každou kostku zvlášť obrázek, do kterého budete zakreslovat síly, které na ni působí.
Nápověda 2 – pohybové rovnice skalárně, vztahy mezi tahy vláken, třecími a tlakovými silami
Zvolte vhodně souřadný systém a přepište pohybové rovnice skalárně. Uvědomte si, jaké vztahy budou mezi některými tahy vláken, třecími a tlakovými silami – použijte 3. Newtonův zákon.
Nápověda 3 – třecí síly
Uvědomte si, na čem závisí velikost třecí síly a jak se dá vyjádřit. Vyjádřete velikosti třecích síl \(F_{t_2}\) a \(F_{t_3}\).
Nápověda 4 – výpočet zrychlení a tahových sil vláken
Využijte rovnice (1), (2) a (6). Po dosazení za třecí síly dostanete tři rovnice o třech neznámých. Spočtěte z nich velikost zrychlení a tahové síly vláken T1 a T2.
CELKOVÉ ŘEŠENÍ
Do obrázku nejprve nakreslíme síly působící na jednotlivé kostky a napíšeme pro ně pohybové rovnice.
Síly působící na jednotlivé kostky:
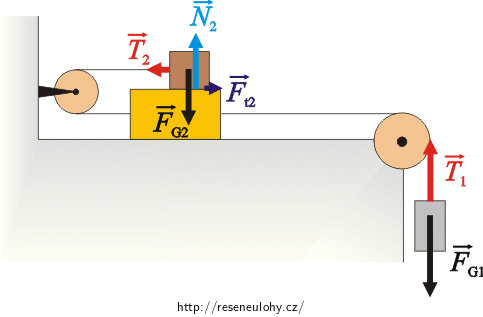
Kostka m1:
\(\vec{F}_\mathrm{G_1}\)…síla tíhová,
\(\vec{T}_{1}\)…tahová síla, kterou na kostku působí vlákno.
Kostka m2:
\(\vec{F}_\mathrm{G_2}\)…síla tíhová,
\(\vec{N}_{2}\)…tlaková síla, kterou na kostku m2 tlačí kostka m3,
\(\vec{T}_{2}\)…tahová síla, kterou na kostku působí vlákno,
\(\vec{F}_\mathrm{t_2}\)…síla třecí mezi kostkami.
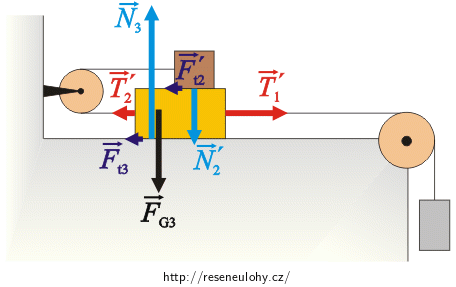
Kostka m3:
\(\vec{F}_\mathrm{G_3}\)…síla tíhová,
\(\vec{T}_{2}\prime\)…tahová síla, kterou na kostku působí vlákno,
\(\vec{T}_{1}\prime\)…tahová síla, kterou na kostku působí vlákno,
\(\vec{F}_\mathrm{t_3}\)…síla třecí mezi kostkou a podložkou,
\(\vec{F}_\mathrm{t_2}\prime\)…síla třecí mezi kostkami,
\(\vec{N}_{2}\prime\)…tlaková síla, kterou na kostku m3 tlačí kostka m2,
\(\vec{N}_{3}\)…tlaková síla, kterou na kostku tlačí podložka.
Pohybové rovnice pro jednotlivé kostky:
Všechny 3 kostky jsou propojeny provázky, pohybují se se stejným zrychlením.
\[m_1:\qquad \vec{F}_\mathrm{G_1} + \vec{T}_1=m_1\vec{a},\] \[m_2:\qquad \vec{F}_\mathrm{G_2}+\vec{N}_2+\vec{F}_\mathrm{t_2}+ \vec{T}_2=m_2\vec{a},\] \[m_3:\qquad \vec{F}_\mathrm{G_3}+\vec{T}_1\prime +\vec{T}_2\prime+\vec{N}_3+\vec{N}_2\prime+\vec{F}_\mathrm{t_3}+\vec{F}_\mathrm{t_2}\prime=m_3\vec{a}.\]Abychom mohli pohybové rovnice přepsat skalárně, zvolíme si souřadný systém os x, y tak, že osu x zvolíme ve směru pohybu kostek. Osa y je kolmá na osu x.
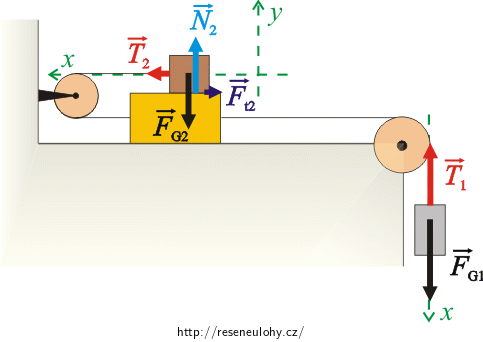
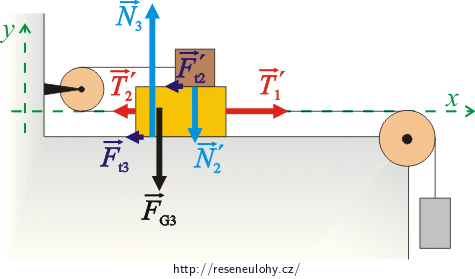
Pohybové rovnice přepíšeme skalárně:
Kostka m1:
\[x:\qquad F_\mathrm{G_1} - T_1\,=\,m_1a.\tag{1}\]Kostka m2:
\[x:\qquad T_2-F_\mathrm{t_2}\,=\,m_2a,\tag{2}\] \[y:\qquad N_2-F_\mathrm{G_2}\,=\,0.\tag{3}\]Kostka m3:
\[x:\qquad T_1\prime-T_2\prime-F_\mathrm{t_3}-F_\mathrm{t_2}\prime\,=\,m_3a,\tag{4}\] \[y:\qquad N_3-N_2\prime-F_\mathrm{G_3}\,=\,0.\tag{5}\]Ve směru osy y se kostky nepohybují, proto je zrychlení rovno nule.
Tahové síly vláken:
Jelikož hmotnost kladek zanedbáváme, nemají žádný moment setrvačnosti a neovlivňují tahové síly vláken. Kostka m3 působí prostřednictvím vlákna na kostku m2 a kostka m2 zase naopak na kostku m3. Obdobně je tomu s kostkou m1 a m3. Podle 3. Newtonova zákona platí pro velikosti sil:
\[|\vec{T}_1| \,=\, |\vec{T}_1\prime|,\] \[|\vec{T}_2| \,=\, |\vec{T}_2\prime|.\]Třecí síly:
Kostka m3 působí třecí silou na kostku m2 a naopak kostka m2 působí opačným směrem třecí silou na kostku m3. Podle 3. Newtonova zákona platí:
\[|\vec{F}_\mathrm{t_2}| \,=\, |\vec{F}_\mathrm{t_2}\prime|.\]
Tlakové síly:
Kostka m3 působí tlakovou silou na kostku m2 a naopak kostka m2 působí opačným směrem tlakovou silou na kostku m3. Podle 3. Newtonova zákona platí:
\[|\vec{N}_2| \,=\, |\vec{N}_2\prime|.\]Přepíšeme rovnice (4) a (5):
\[x:\qquad T_1-T_2-F_\mathrm{t_3}-F_\mathrm{t_2}\,=\,m_3a,\tag{6}\] \[y:\qquad N_3-N_2-F_\mathrm{G_3}\,=\,0.\tag{7}\]Vyjádření třecích sil:
Třecí síla \(F_\mathrm{t_2}\) je úměrná síle, kterou tlačí kostka m2 na kostku m3. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí kostka m3 na kostku m2.
Třecí sílu \(F_\mathrm{t_2}\) můžeme tedy vyjádřit jako:
\[F_\mathrm{t_2} \,=\, N_2f.\]Dosadíme za \(N_2\) ze vztahu (3):
\[F_\mathrm{t_2} \,=\, F_\mathrm{G_2}f\,=\,m_2gf.\tag{8}\]Třecí síla \(F_\mathrm{t_3}\) je úměrná síle, kterou tlačí kostka m3 na stůl. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí stůl na kostku m3.
Třecí sílu \(F_\mathrm{t_3}\) můžeme tedy vyjádřit jako:
\[F_\mathrm{t_3} \,=\, N_3f.\]
Dosadíme za \(N_3\) ze vztahu (7):
\[F_\mathrm{t_3} \,=\, (N_2+F_\mathrm{G_3)}f\,=\,(F_\mathrm{G_2}+F_\mathrm{G_3})f,\] \[F_\mathrm{t_3} \,=\, (m_2+m_3)gf.\tag{9}\]Přepíšeme rovnice (1), (2) a (6), do rovnice (2) dosadíme třecí sílu \(F_\mathrm{t_2}\) a do rovnice (6) dosadíme třecí síly \(F_\mathrm{t_2}\) a \(F_\mathrm{t_3}\):
\[m_1g - T_1\,=\,m_1a,\tag{10}\] \[T_2-m_2gf\,=\,m_2a,\tag{11}\] \[T_1-T_2-(m_2+m_3)gf-m_2gf\,=\,m_3a.\tag{12}\]Výpočet zrychlení:
Sečteme rovnice (10) – (12).
\[m_1g-m_2gf-m_3gf-2m_2gf\,=\,\left(m_3+m_2+m_1\right)a,\] \[m_1g-m_3gf-3m_2gf\,=\,\left(m_3+m_2+m_1\right)a,\]\[a\,=\,\frac{g\left(m_1-m_3f-3m_2f\right)}{m_3+m_2+m_1}.\tag{13}\]
Výpočet tahové síly vlákna T1:
Vyjádříme sílu T1 ze vztahu (10):
\[T_1\,=\,m_1g-m_1a\,=\,m_1g-m_1\frac{m_1g-m_3gf-3m_2gf}{m_3+m_2+m_1}.\]
Převedeme na společného jmenovatele:
\[T_1\,=\,\frac{m_1^2g+m_1m_2g+m_1m_3g-m_1^2g+m_1m_3gf+3m_1m_2gf} {m_3+m_2+m_1},\] \[T_1\,=\,\frac{m_1m_3gf+3m_1m_2gf+m_1m_2g+m_1m_3g} {m_3+m_2+m_1},\] \[T_1\,=\,\frac{m_1g\left[m_3(f+1)+ m_2(3f+1)\right]} {m_3+m_2+m_1}.\tag{14}\]Výpočet tahové síly vlákna T2:
Vyjádříme sílu T2 ze vztahu (11):
\[T_2\,=\,m_2a\,+\,m_2gf\,=\,m_2\frac{m_1g-m_3gf-3m_2gf} {m_3+m_2+m_1}\,+\,m_2gf.\]Převedeme na společného jmenovatele:
\[T_2\,=\,\frac{m_1m_2g-m_2m_3gf-3m_2^2gf+m_1m_2gf+m_2^2gf+m_2m_3gf} {m_3+m_2+m_1},\] \[T_2\,=\,\frac{m_1m_2g-2m_2^2gf+m_1m_2gf} {m_3+m_2+m_1},\] \[T_2\,=\,\frac{m_2g\left[m_1(1+f)-2m_2f\right]} {m_3+m_2+m_1}.\tag{15}\]CELKOVÁ ODPOVĚĎ
Velikost zrychlení kostek je \[a\,=\,\frac{g\left(m_1-m_3f-3m_2f\right)}{m_3+m_2+m_1}.\]
Velikost tahové síly napínající vlákno mezi kostkami m2 a m3 je
\[T_1\,=\,\frac{m_1g\left[m_3\left(f+1\right)+ m_2\left(3f+1\right)\right]}{m_3+m_2+m_1}\,.\]Velikost tahové síly napínající vlákno mezi kostkami m3 a m1 je
\[T_2\,=\,\frac{m_2g\left[m_1\left(1+f\right)-2m_2f\right]}{m_3+m_2+m_1}\,.\]




