Pohyb po dvou nakloněných rovinách
Úloha číslo: 1132
V homogenním tíhovém poli jsou umístěny dvě nakloněné roviny, navzájem kolmé, stýkající se horními okraji. Jedna z rovin svírá s vodorovnou podložkou úhel α. Ve stejný okamžik vypustíme ze společné hrany na opačné strany dvě koule o hmotnostech m1, m2 a poloměru R. Určete pohyb těžiště soustavy těchto dvou koulí. Úlohu řešte:
Nápověda 1 – k části A
V první části úlohy budeme zanedbávat moment setrvačnosti koulí – lze v takovém případě koule nahradit nějakým jednodušším fyzikálním modelem?
Nápověda 2 – k části A
Zakreslete situaci do obrázku a vhodně zaveďte souřadný systém. Co znamená zadání „určete pohyb těžiště“? Co má být vlastně výstupem úlohy?
Nápověda 3 – k části A
Předpokládejme, že koule sjíždějí dolů bez tření. Jak velké zrychlení budou koule mít? Nakreslete do obrázku všechny síly, které na koule působí, a pomocí 2. Newtonova zákona najděte příslušná zrychlení. Jaký pohyb budou jednotlivé koule vykonávat (z hlediska trajektorie a rychlosti)?
Nápověda 4 – k části A
Pro kouli o hmotnosti m1 napište závislost její x-ové a y-ové souřadnice na čase. Tento postup pak opakujte i pro kouli o hmotnosti m2.
Nápověda 5 – k části A
V tuto chvíli již víme, jak se s časem mění souřadnice našich dvou koulí (hmotných bodů). Nyní použijte vztah pro určení polohy těžiště soustavy hmotných bodů a první část úlohy dopočítejte.
Nápověda 6 – k části B
Ve druhé části úlohy započítáme moment setrvačnosti koulí. Nejdříve si ale projděte postup části A a rozhodněte, kam až ho můžeme zopakovat – kde se nenulový moment setrvačnosti poprvé projeví?
Nápověda 7 – k části B
K určení velikostí zrychlení těžiště koulí ve směrech jednotlivých souřadných os použijte zákon zachování mechanické energie. (Pozor, jedná se o poměrně dlouhý výpočet spojující poznatky z různých oblastí mechaniky!)
Komentář 1
Velikosti zrychlení těžiště obou koulí můžeme určit i jiným postupem, a to pomocí impulsových vět (viz např. úloha Kutálející se obruč, postup B).
Nápověda 8 – k části B
V předchozím kroku jsme získali velikosti zrychlení těžiště první koule ax a druhé koule ay. Pracujte s nimi dále jako se složkami a1 a a2 v části A a pomocí stejných výpočtů určete, jak se s časem mění souřadnice xT´(t), yT´(t) těžiště soustavy.
Celkové řešení – část A
Zanedbáváme-li v úloze moment setrvačnosti koulí, lze koule nahradit hmotnými body. Vhodné umístění problému do souřadného systému ukazuje obrázek níže.
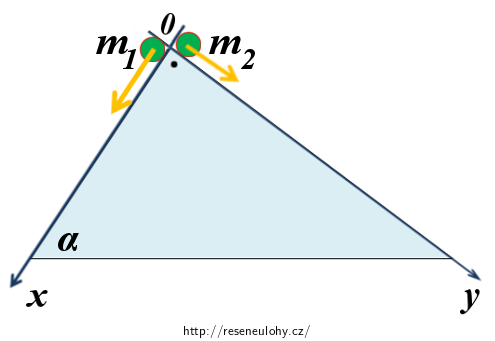
Uvažujeme, že pohyb probíhá v rovině xy, uvažovat změnu z-ové souřadnice tedy nemusíme. Výstupem úlohy by tak mělo být nalezení předpisu, který popisuje vývoj souřadnic těžiště xT a yT na čase, tj. xT(t) = ?, yT(t) = ?
Na obě koule působí tíhová síla a tlaková síla podložky. Jejich výslednice udílí kouli o hmotnosti m1 zrychlení ve směru osy x a kouli o hmotnosti m2 zrychlení ve směru osy y. Obrázek níže zachycuje nejen působící tíhové síly FG a tlakové síly FN, ale také rozklad tíhové síly do směru souřadných os (černě).

Podle 2. Newtonova zákona platí pro kouli o hmotnosti m1:
\[ \vec{F}_\mathrm{G1}\,+\,\vec{F}_\mathrm{N1}\,=\,m_1\vec{a}_1.\tag{1}\]Podle obrázku rozepíšeme vztah (1) skalárně:
Směr osy x:
\[F_\mathrm{G1}\sin{\alpha}\,=\,m_1a_1.\tag{2}\]Směr osy y:
\[F_\mathrm{G1}\cos{\alpha}\,-\,F_\mathrm{N1}\,=\,0.\tag{3}\]Dosazením za velikost tíhové síly dostáváme ze vztahu (2):
\[m_1g\sin{\alpha}\,=\,m_1a_1\,\Rightarrow\,a_1\,=\,g\sin{\alpha}.\tag{4}\]Koule o hmotnosti m1 se tedy bude pohybovat rovnoměrně zrychleným pohybem ve směru osy x se zrychlením a1. Analogicky nyní budeme postupovat v případě druhé koule.
Podle 2. Newtonova zákona platí pro kouli o hmotnosti m2:
\[ \vec{F}_\mathrm{G2}\,+\,\vec{F}_\mathrm{N2}\,=\,m_2\vec{a}_2.\tag{5}\]Podle obrázku rozepíšeme vztah (5) skalárně:
Směr osy x:
\[F_\mathrm{G2}\sin{\alpha}\,-\,F_\mathrm{N2}\,=\,0.\tag{6}\]Směr osy y:
\[F_\mathrm{G2}\cos{\alpha}\,=\,m_2a_2.\tag{7}\]Dosazením za velikost tíhové síly dostáváme ze vztahu (7):
\[m_2g\cos{\alpha}\,=\,m_2a_2\,\Rightarrow\,a_2\,=\,g\cos{\alpha}.\tag{8}\]Také koule o hmotnosti m2 se tedy bude pohybovat rovnoměrně zrychleným pohybem, tentokrát ovšem se zrychlením a2 ve směru osy y.
Koule o hmotnosti m1 vykonává ve směru osy x rovnoměrně zrychlený pohyb se zrychlením a1:
\[x_1(t)\,=\,\frac{1}{2}a_1t^2\,=\,\frac{1}{2}g(\sin{\alpha})t^2.\tag{9}\]Ve směru osy y je souřadnice koule identicky nulová:
\[y_1(t)\,=\,0.\tag{10}\]Koule o hmotnosti m2 vykonává ve směru osy y rovnoměrně zrychlený pohyb se zrychlením a2:
\[y_2(t)\,=\,\frac{1}{2}a_2t^2\,=\,\frac{1}{2}g(\cos{\alpha})t^2.\tag{11}\]Ve směru osy x je souřadnice koule nulová:
\[x_2(t)\,=\,0.\tag{12}\]Vztah pro polohu těžiště soustavy n hmotných bodů vypadá následovně:
\[\vec{r}_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}\vec{r}_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}},\]kde mi jsou hmotnosti jednotlivých hmotných bodů a ri jim příslušející polohové vektory.
Protože souřadnice těžiště lze počítat po složkách, platí po dosazení ze vztahů (9) a (12) pro x-ovou souřadnici těžiště naší soustavy:
\[x_\mathrm{T}(t)\,=\,\frac{\sum_{i=1}^2{m_\mathrm{i}x_\mathrm{i}(t)}}{\sum_{i=1}^2{m_\mathrm{i}}}\,=\,\frac{m_1x_1(t)\,+\,m_2x_2(t)} {m_1\,+\,m_2}\,=\,\frac{m_1g(\sin{\alpha})t^2}{2(m_1\,+\,m_2)}.\]Analogicky pro y-ovou souřadnici těžiště platí po dosazení ze vztahů (10) a (11):
\[y_\mathrm{T}(t)\,=\,\frac{\sum_{i=1}^2{m_\mathrm{i}y_\mathrm{i}(t)}}{\sum_{i=1}^2{m_\mathrm{i}}}\,=\,\frac{m_1y_1(t)\,+\,m_2y_2(t)} {m_1\,+\,m_2}\,=\,\frac{m_2g(\cos{\alpha})t^2}{2(m_1\,+\,m_2)}.\]Souřadnice těžiště se tedy v námi zvoleném souřadném systému mění s časem podle těchto vztahů:
\[x_\mathrm{T}(t)\,=\,\frac{m_1g(\sin{\alpha})t^2}{2(m_1\,+\,m_2)},\] \[y_\mathrm{T}(t)\,=\,\frac{m_2g(\cos{\alpha})t^2}{2(m_1\,+\,m_2)},\] \[z_\mathrm{T}(t)\,=\,0.\]Celkové řešení – část B
Souřadný systém zavedeme analogicky jako v části A, snad jen s tím rozdílem, že obě osy budeme vést rovnoběžně s povrchem nakloněných rovin ve vzdálenosti R od něj – tím zajistíme, že y-ová souřadnice první koule a x-ová souřadnice druhé koule zůstanou během pohybu nulové (viz obrázek).
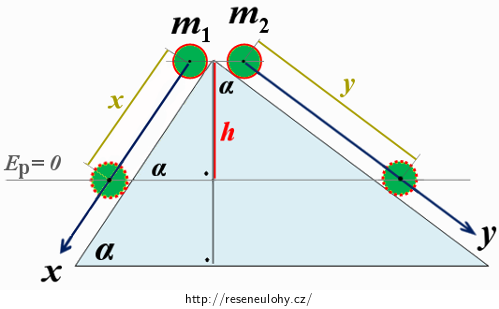
Nenulový moment setrvačnosti J koulí se projeví v okamžiku, kdy budeme určovat zrychlení ve směru jednotlivých os. Část potenciální energie koule Ep se při pohybu po nakloněné rovině přemění na kinetickou rotační energii Er, čímž zbývá méně energie na kinetickou energii posuvného pohybu koule Ek. Koule se tedy pohybuje s menším zrychlením, než když jsme její moment setrvačnosti zanedbávali.
K nalezení velikosti zrychlení těžiště koulí využijeme zákon zachování mechanické energie.
Vybereme dvě situace a napíšeme, jakou celkovou mechanickou energii v nich jednotlivé koule mají. Hladinu nulové potenciální energie volíme v hloubce h pod místem vypuštění (viz obrázek výše).
Pro kouli o hmotnosti m1:
Situace 1 – okamžik vypuštění:
\[E_1\,=\,E_\mathrm{p1},\tag{13}\]kde Ep1 je potenciální energie koule o hmotnosti m1.
Situace 2 – hmotný střed koule urazil dráhu x:
\[E_2\,=\,E_\mathrm{r1}\,+\,E_\mathrm{k1},\tag{14}\]kde Er1 je kinetická energie rotačního pohybu koule o hmotnosti m1 vzhledem k ose procházející jejím středem a Ek1 kinetická energie jejího posuvného pohybu.
Podle zákona zachování mechanické energie platí:
\[E_1\,=\,E_2.\tag{15}\]Tedy po dosazení ze vztahů (13) a (14):
\[E_\mathrm{p1}\,=\,E_\mathrm{r1}\,+\,E_\mathrm{k1}.\tag{16}\]Ze známých vztahů pro výpočty těchto jednotlivých energií do vztahu (16) dosadíme:
\[m_1gh\,=\,\frac{1}{2}m_1v^2_\mathrm{x}\,+\,\frac{1}{2}J{\omega_1}^2,\tag{17}\]kde vx je rychlost těžiště koule, J moment setrvačnosti vzhledem k ose procházející středem koule a ω1 její úhlová rychlost.
Pro moment setrvačnosti homogenní koule o hmotnosti m1 a poloměru R vzhledem k ose procházející jejím středem platí:
\[J\,=\,\frac{2}{5}m_1R^2.\tag{18}\]Z obrázku vidíme:
\[\sin{\alpha}\,=\,\frac{h}{x}\,\Rightarrow\,h\,=\,x\sin{\alpha}.\tag{19}\]Velikost zrychlení těžiště první koule označíme ax. Ze vztahů pro rovnoměrně zrychlený pohyb víme:
\[x\,=\,\frac{1}{2}a_\mathrm{x}t^2,\tag{20}\] \[v_\mathrm{x}\,=\,a_\mathrm{x}t.\tag{21}\]Z vlastností rotačního pohybu s úhlovou rychlostí ω1:
\[\omega_1\,=\,\frac{v_\mathrm{x}}{R}.\tag{22}\]Vztahy (18) až (22) nyní dosadíme do rovnosti (17):
\[m_1g{\cdot}\frac{1}{2}a_\mathrm{x}t^2\sin{\alpha}\,=\,\frac{1}{2}m_1(a_\mathrm{x}t)^2\,+\,\frac{1}{2}{\cdot}\frac{2}{5}m_1R^2{(\frac{a_\mathrm{x}t}{R})^2}.\tag{23}\]Po úpravě vztahu (23) dostáváme:
\[a_\mathrm{x}\,=\,\frac{5}{7}g\sin{\alpha}.\tag{24}\]Analogicky můžeme postupovat v případě koule o hmotnosti m2, pouze funkci sinus nahradí ve výpočtu výšky h funkce kosinus.
Pro kouli o hmotnosti m2:
Zákon zachování mechanické energie má tento tvar:
\[E_\mathrm{p2}\,=\,E_\mathrm{r2}\,+\,E_\mathrm{k2},\tag{25}\]kde Ep2 je potenciální energie koule o hmotnosti m2, Er2 je kinetická energie rotačního pohybu této koule vzhledem k ose procházející jejím středem a Ek2 kinetická energie jejího posuvného pohybu. Potenciální energii počítáme v okamžiku vypuštění, obě kinetické energie po uražení dráhy y (analogicky jako v případě první koule). Ze známých vztahů pro výpočty těchto jednotlivých energií do vztahu (25) dosadíme:
\[m_2gh\,=\,\frac{1}{2}m_2v^2_\mathrm{y}\,+\,\frac{1}{2}J{\omega_2}^2,\tag{26}\]kde vy je rychlost těžiště koule, J moment setrvačnosti vzhledem k ose procházející středem koule a ω2 její úhlová rychlost.
Moment setrvačnosti druhé koule určíme stejně jako u koule první pomocí vztahu (18) (samozřejmě s hmotností m2), mění se ale geometrie úlohy:
\[\cos{\alpha}\,=\,\frac{h}{y}\,\Rightarrow\,h\,=\,y\cos{\alpha}.\tag{27}\]Velikost zrychlení těžiště první koule označíme ay. Ze vztahů pro rovnoměrně zrychlený pohyb víme:
\[y\,=\,\frac{1}{2}a_\mathrm{y}t^2,\tag{28}\] \[v_\mathrm{y}\,=\,a_\mathrm{y}t.\tag{29}\]A z vlastností rotačního pohybu s úhlovou rychlostí ω2:
\[\omega_2\,=\,\frac{v_\mathrm{y}}{R}.\tag{30}\]Vztahy (27) až (30) nyní dosadíme do rovnosti (26):
\[m_2g{\cdot}\frac{1}{2}a_\mathrm{y}t^2\cos{\alpha}\,=\,\frac{1}{2}m_2(a_\mathrm{y}t)^2\,+\,\frac{1}{2}{\cdot}\frac{2}{5}m_2R^2{(\frac{a_\mathrm{y}t}{R})^2}.\tag{31}\]Po úpravě vztahu (31) dostáváme:
\[a_\mathrm{y}\,=\,\frac{5}{7}g\cos{\alpha}.\tag{32}\]Poznámka: Velikosti zrychlení těžiště obou koulí můžeme určit i jiným postupem, a to pomocí impulsových vět (viz např. úloha Kutálející se obruč, postup B).
Dále budeme opakovat postup popsaný v nápovědách (5) a (6), pouze dosadíme jiné hodnoty zrychlení.
Těžiště koule o hmotnosti m1 vykonává ve směru osy x rovnoměrně zrychlený pohyb se zrychlením ax:
\[x_1´(t)\,=\,\frac{1}{2}a_\mathrm{x}t^2\,=\,\frac{5}{14}g(\sin{\alpha})t^2.\]Ve směru osy y je souřadnice koule nulová:
\[y_1´(t)\,=\,0.\]Těžiště koule o hmotnosti m2 vykonává ve směru osy y rovnoměrně zrychlený pohyb se zrychlením ay:
\[y_2´(t)\,=\,\frac{1}{2}a_\mathrm{y}t^2\,=\,\frac{5}{14}g(\cos{\alpha})t^2.\]Ve směru osy x je souřadnice koule identicky nulová:
\[x_2´(t)\,=\,0.\]Souřadnice těžiště soustavy lze počítat po složkách:
\[x_\mathrm{T}´(t)\,=\,\frac{\sum_{i=1}^2{m_\mathrm{i}x_\mathrm{i}´(t)}}{\sum_{i=1}^2{m_\mathrm{i}}}\,=\,\frac{m_1x_1´(t)\,+\,m_2x_2´(t)} {m_1\,+\,m_2}\,=\,\frac{5m_1g(\sin{\alpha})t^2}{14(m_1\,+\,m_2)},\] \[y_\mathrm{T}´(t)\,=\,\frac{\sum_{i=1}^2{m_\mathrm{i}y_\mathrm{i}´(t)}}{\sum_{i=1}^2{m_\mathrm{i}}}\,=\,\frac{m_1y_1´(t)\,+\,m_2y_2´(t)} {m_1\,+\,m_2}\,=\,\frac{5m_2g(\cos{\alpha})t^2}{14(m_1\,+\,m_2)}.\]Souřadnice těžiště se tedy v námi zvoleném souřadném systému mění s časem podle těchto vztahů:
\[x_\mathrm{T}´(t)\,=\,\frac{5m_1g(\sin{\alpha})t^2}{14(m_1\,+\,m_2)},\] \[y_\mathrm{T}´(t)\,=\,\frac{5m_2g(\cos{\alpha})t^2}{14(m_1\,+\,m_2)},\] \[z_\mathrm{T}´(t)\,=\,0.\]Odpověď
Část A: (Zanedbáváme moment setrvačnosti koulí.)
Souřadnice těžiště se tedy v námi zvoleném souřadném systému mění s časem podle těchto vztahů:
\[x_\mathrm{T}(t)\,=\,\frac{m_1g(\sin{\alpha})t^2}{2(m_1\,+\,m_2)},\] \[y_\mathrm{T}(t)\,=\,\frac{m_2g(\cos{\alpha})t^2}{2(m_1\,+\,m_2)},\] \[z_\mathrm{T}(t)\,=\,konst.\]Část B: (Uvažujeme moment setrvačnosti koulí.)
Souřadnice těžiště se tedy v námi zvoleném souřadném systému mění s časem podle těchto vztahů:
\[x_\mathrm{T}´(t)\,=\,\frac{5m_1g(\sin{\alpha})t^2}{14(m_1\,+\,m_2)},\] \[y_\mathrm{T}´(t)\,=\,\frac{5m_2g(\cos{\alpha})t^2}{14(m_1\,+\,m_2)},\] \[z_\mathrm{T}´(t)\,=\,konst.\]Komentář 2
Výsledek má samozřejmě smysl pro taková t, než se první z koulí dotkne vodorovné podložky.



