Kulička v medu
Úloha číslo: 16
Ocelovou kuličku o hmotnosti m položíme do sklenice s medem. Odporová síla Fodp působící na kuličku je přímo úměrná její rychlosti.
1) Určete, jak velkou maximální rychlost vmax může kulička dosáhnout.
2) Určete průběh velikosti rychlosti v(t) kuličky.

Poznámka: Místo velikost rychlosti píšeme dále jen rychlost.
Zápis
m hmotnost kuličky V objem kuličky ρm hustota medu \(\vec{F}_\mathrm{odp}\) odporová síla působící na kuličku k konstanta přímé úměrnosti g = 9,81 m·s−2 tíhové zrychlení vmax = ? maximální rychlost, jakou může kulička dosáhnout v(t) = ? časový průběh velikosti rychlosti kuličky Nápověda 1 – síly působící na kuličku, pohybová rovnice
Rozmyslete si nejprve, které síly na kuličku působí a zda se bude jejich velikost během pohybu měnit. Nakreslete si obrázek.
Jak se bude měnit výslednice těchto sil?
Jak se bude měnit zrychlení a rychlost kuličky?
Nápověda 2 – maximální rychlost
Jaká je výslednice sil v okamžiku, kdy kulička dosáhne maximální rychlosti? Zapište to rovnicí.
Nápověda 3 – pohybová rovnice, průběh v(t)
Podívejte se na obrázek se silami působícími na kuličku a napište pro ni pohybovou rovnici.
CELKOVÉ ŘEŠENÍ
Nejprve si rozmyslíme, jaké síly působí na kuličku a zda se během pohybu mění jejich velikost, a zjistíme maximální rychlost kuličky.
Síly působící na kuličku jsou 3:
\(\vec{F}_\mathrm{odp}\)…síla odporová \(\vec{F}_\mathrm{G}\)…síla tíhová \(\vec{F}_\mathrm{vz}\)…síla vztlakováVztahy pro velikosti předchozích sil:
Fodp = kv…narůstá spolu s rychlostí
FG = mg…zůstává konstantní
Fvz = Vρmg…zůstává konstantní
k…konstanta přímé úměrnosti
g…tíhové zrychlení o velikosti 9,81 m·s−2
V…objem kuličky
ρm…hustota medu
Jak se mění velikost výsledné síly, zrychlení a rychlost během pohybu kuličky:
1. Na počátku pohybu je rychlost kuličky, a tedy i odporová síla nulová. Vzhledem k tomu, že hustota oceli je větší než hustota medu, směřuje výsledná síla dolů, stejně tak zrychlení a rychlost kuličky narůstá.
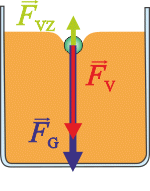
2. S tím, jak narůstá rychlost kuličky, zvětšuje se i odporová síla, velikost výsledné síly směřující dolů se zmenšuje, stejně jako velikost zrychlení. Rychlost kuličky stále narůstá, ale čím dál tím pomaleji.
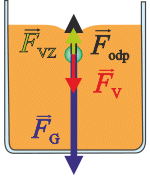
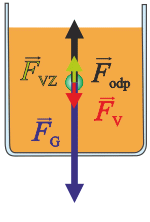
3. V jistém okamžiku odporová síla dosáhne takové velikosti, že se síly vyrovnají, zrychlení je nulové a kulička se dál pohybuje konstantní rychlostí.
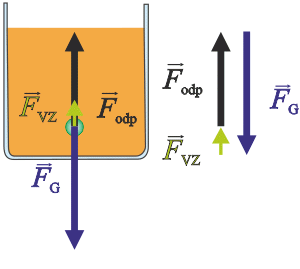
V okamžiku, kdy kulička dosáhne maximální rychlosti, je výsledná síla, která na ni působí, nulová.
Pro síly působící na kuličku platí:
\[\vec{F}_\mathrm{G}+\vec{F}_\mathrm{odp}+\vec{F}_\mathrm{vz}\,=\,0\tag{1}\]Rovnici (1) přepíšeme skalárně:
\[F_\mathrm{G}-F_\mathrm{odp}-F_\mathrm{vz}\,=\,0\,.\tag{2}\]V rovnici (2) rozepíšeme síly:
\[mg\,-\,kv_\mathrm{max}\,-\,V\rho_\mathrm{m}g\,=\,0\,.\tag{3}\]Maximální rychlost:
Z rovnice (3) si vyjádříme vmax:
\[v_\mathrm{max}\,=\,\frac{mg-V\rho_\mathrm{m}g}{k}\,.\]Za objem V můžeme ještě dosadit \[V\,=\,\frac{m}{\rho_\mathrm{k}}\]
ρk…hustota kuličky
\[v_\mathrm{max}\,=\,\frac{mg\,-\,m\frac{\rho_\mathrm{m}}{\rho_\mathrm{k}}g}{k}\,.\tag{4}\]Nyní zjistíme časový průběh velikosti rychlosti kuličky. Vyjdeme z její pohybové rovnice.
Pohybová rovnice pro kuličku:
\[\vec{F}_\mathrm{G}+\vec{F}_\mathrm{odp}+\vec{F}_\mathrm{vz}\,=\, m\vec{a}\tag{5}\]Souřadný systém zvolíme tak, že osu y zorientujeme dolů ve směru pohybu kuličky a rovnici (5) přepíšeme skalárně:
\[F_\mathrm{G}-F_\mathrm{odp}-F_\mathrm{vz}\,=\,ma.\tag{6}\]V rovnici (6) rozepíšeme síly:
\[mg-kv-V\rho_\mathrm{m}g\,=\,ma.\tag{7}\]Ve vztahu (7) přepíšeme zrychlení a jako změnu rychlosti za čas.
Průběh v(t):
\[mg-kv-V\rho_\mathrm{m}g\,=\,m\frac{dv}{dt}\tag{8}\]Objem kuličky můžeme vyjádřit:
\[V\,=\,\frac{m}{\rho_\mathrm{k}}\,.\tag{9}\]m…hmotnost kuličky
ρk…hustota kuličky
Vztah (9) dosadíme do rovnice (8):
\[mg-kv-\frac{m}{\rho_\mathrm{k}}\rho_\mathrm{m}g\,=\,m\frac{dv}{dt}.\tag{10}\]Označme si pro zjednodušení zápisu:
\[\frac{m}{\rho_\mathrm{k}}\rho_\mathrm{m}\,=\,m^\prime.\tag{11}\]Vztah (11) dosadíme do vztahu (10):
\[mg-kv-m^\prime g\,=\,m\frac{dv}{dt}.\tag{12}\]Získali jsme diferenciální rovnici 1. řádu s konstantními koeficienty. Vyřešíme ji separací proměnných:
Rovnici nejprve vydělíme m a upravíme:
\[\frac{m-m^\prime}{m}g-\frac{kv}{m}\,=\,\frac{dv}{dt}\] \[-\frac{k}{m}\left(v-\frac{m-m^\prime}{k}g\right)\,=\,\frac{dv}{dt}.\]Nyní separujeme proměnné v a t a rovnici zintegrujeme:
\[-\frac{k}{m}dt\,=\,\frac{dv}{v-\frac{m-m^\prime}{k}g} \hspace{20px}/\int\,\] \[-\frac{k}{m}t + C\,=\,ln|v-\frac{m-m^\prime}{k}g|.\]Rovnici odlogaritmujeme:
\[e^{\left(-\frac{k}{m}t+C\right)} \,=\,|v-\frac{m-m^\prime}{k}g|\,\] \[e^{-\frac{k}{m}t}\cdot e^{C} \,=\,|v-\frac{m-m^\prime}{k}g|.\]Konstantu eC označíme jako K:
\[e^{-\frac{k}{m}t}\cdot K\,=\,|v-\frac{m-m^\prime}{k}g|\,.\tag{13}\]Výraz \[\frac{m-m^\prime}{k}g\] je roven vztahu (4), který jsme spočítali pro maximální rychlost: \[v_\mathrm{max}\,=\,\frac{mg-m\frac{\rho_\mathrm{m}}{\rho_\mathrm{k}}g}{k}.\]
Pro rychlost v platí, že v ≤ vmax, proto:
\[|v-\frac{m-m^\prime}{k}g|\,=\,-v+\frac{m-m^\prime}{k}g\,.\]Hodnotu konstanty K zjistíme z počátečních podmínek. Pro t = 0 s je v = 0 m·s−1, platí tedy:
\[e^0\cdot K\,=\,-0+\frac{m-m^\prime}{k}g\,\] \[K\,=\,\frac{m-m^\prime}{k}g.\]Dosadíme do vztahu (13):
\[\frac{m-m^\prime}{k}ge^{-\frac{k}{m}t}\,=\,-v+\frac{m-m^\prime}{k}g\,\] \[v(t)\,=\,\frac{m-m^\prime}{k}g\left(1-e^{-\frac{k}{m}t}\right).\tag{14}\]CELKOVÁ ODPOVĚĎ
Kulička může dosáhnout maximální rychlosti \[v_\mathrm{max}\,=\,\frac{mg\,-\,m\frac{\rho_\mathrm{m}}{\rho_\mathrm{k}}g}{k}.\]
Průběh velikosti rychlosti kuličky v závislosti na čase je dán vztahem \[v(t)\,=\,\frac{m-m\prime}{k}g(1-e^{-\frac{k}{m}t})\,.\]



