Havárie ropovodu

Úloha číslo: 943

Ropovod IKL (Ingolstadt, Kralupy, Litvínov), který dodává ropu pro Českou republiku, má přepravní kapacitu 1510 m³ ropy za hodinu. Poloměr trubek ropovodu je 35 cm. Havarijní technici vypočítávají, kolik ropy by vyteklo do okolí při jejím úniku. Počítají, že by ropa vytékala otvorem ven z trubek. Odstavení celé trasy ropovodu a uzavření všech ventilů trvá 15 minut. Uvažujeme, že rychlost ropy v trubce je stálá. Vypočítejte:

a) Jakou rychlostí ropa teče trubkou ropovodu?

b) Kolik tun ropy by otvorem uniklo do okolí během havárie? (Hustota ropy je asi 840 kg/m³.)

c) Kolik automobilových nádrží by šlo naplnit benzinem vyrobeným z ropy uniklé při havárii? (Počítejte s objemem nádrže osobního auta 55 l). Benzin se vyrábí se zhruba poloviční výtěžností – z 1 l ropy se vyrobí 0,5 l benzinu.

d) Kolik tun ropy se ropovodem přepraví za rok?

Zápis

A = 1510 m³	přepravní kapacita ropovodu
r = 35 cm = 0,35 cm	poloměr trubek ropovodu
t = 15 min = 900 s	doba potřebná k odstavení ventilů
ρ = 840 kg/m³	hustota ropy
V₁ = 55 l = 0,055 m³	objem jedné automobilové nádrže

Nápověda 1 - k části a)
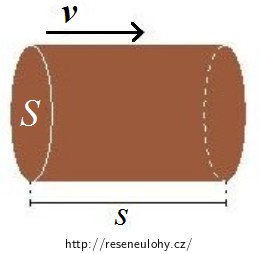
Jaké těleso tvoří ropa, která proteče trubkou za 15 minut? Napoví vám obrázek.
Řešení nápovědy 1 – k části a)
Ropa, která proteče trubkou za 15 minut, tvoří válec. Tento válec má obsah podstavy rovný průřezu trubky S. Výška válce je rovna dráze s, kterou ropa (vybraný atom) urazí za daný čas, tedy 15 minut.
Nápověda 2 – k části a)
Jak určíme objem takového válce?
Řešení nápovědy 2 – k části a)
Objem válce určíme podle vzorce:
\[V\,=\,S{\cdot}s\,,\tag{1}\]
kde S je průřez trubky ropovodu (resp. jeho obsah) a s je vzdálenost, o kterou se ropa posune za 15 minut.
Nápověda 3 – k části a)
Jak určíme vzdálenost, o kterou se ropa v trubce za 15 minut posune? Uvědomte si, že se ropa pohybuje rychlostí, která je stálá, nemění se. Jaký je to pohyb?
Řešení nápovědy 3 – k části a)
Ropa se pohybuje rovnoměrným pohybem, pro dráhu rovnoměrného pohybu platí:
\[s\,=\,v{\cdot}t\,,\tag{2}\]
kde v je rychlost tohoto pohybu a t doba pohybu (v našem případě 15 min).
Nápověda 4 – k části a)
Dosaďte ze vzorce (2) do (1) a rozmyslete si, které veličiny znáte a kterou chcete určit. Neznámou veličinu ze vzorce vyjádřete.
Řešení nápovědy 4 – k části a)
Dosazením do vztahu (1) získáme:
\[V\,=\,S {\cdot} v{\cdot} t\,,\tag{3}\]
kde S je průřez trubky ropovodu (resp. jeho obsah), v je rychlost, kterou ropa teče, a t doba pohybu ropy (v našem případě 15 min).

Neznámou veličinou je rychlost v:
\[v\,=\,\frac {V}{S{\cdot} t}\,,\tag{4}\]
kde V je objem ropy, která proteče ropovodem za 15 minut, S je průřez trubky ropovodu (resp. jeho obsah) a t doba pohybu ropy (v našem případě 15 min).
Nápověda 5 – k části a)
Co ještě potřebujeme zjistit, abychom ze vzorce (4) mohli vypočítat rychlost ropy v trubce?
Řešení nápovědy 5 – k části a)
Potřebujeme zjistit obsah průřezu trubky S a objem V – jaký objem ropy proteče ropovodem za 15 minut.
Nápověda 6 – k části a)
Víme, že ropovodem proteče 1510 m³ ropy za hodinu. Jak určíme objem ropy, který proteče za 15 minut? Určete ho.
Řešení nápovědy 6 – k části a)
Objem ropy, která proteče ropovodem za 15 minut, určíme trojčlenkou:

za 60 minut……………1510 m³ ropy

za 15 minut……………V m³ ropy
------------------------------------------------------
\(\frac{V}{1510}\,=\,\frac{15}{60}\,,\)

tedy \(V\,=\,\frac{1510{\cdot}15}{60}\,\,\mathrm{m}^3\,=\,377{,}5\,\mathrm{m}^3.\)

Za 15 minut proteče ropovodem 377,5 m³ ropy.

Nebo si stačí uvědomit, že 15 min je čtvrtina hodiny a tedy:
\[V\,=\,\frac{1510}{4}\,\mathrm{m}^3\,=\,377{,}5\,\mathrm{m}^3\,.\]
Nápověda 7 – k části a)
Určete obsah průřezu trubky S.
Řešení nápovědy 7 – k části a)
Známe poloměr trubky r, takže můžeme vypočítat obsah průřezu jako obsah kruhu s poloměrem r:
\[S\,=\,{\pi}r^2\,.\tag{5}\]
Číselně:
\[S\,=\,{\pi}{\cdot}(0{,}35)^2\,\mathrm{m}^2\,\dot=\,0{,}38\,\mathrm{m}^2\,.\]
Nápověda 8 – k části a)
Nyní už znáte všechny potřebné veličiny ve vztahu (4). Dopočítejte tedy rychlost ropy v ropovodu. (Nezapomeňte převést čas z minut na sekundy.)
Řešení nápovědy 8 – k části a)
Rychlost ropy spočítáme dosazením do vzorce (4). Číselně:
\[v\,=\,\frac{V}{S{\cdot}t}\,=\,\frac{377{,}5}{0{,}38{\cdot}15{\cdot}60} \,\mathrm{m\cdot s^{-1}}\,\dot=\,1{,}1\,\mathrm{m\cdot s^{-1}}\,.\]
Ropa teče ropovodem rychlostí přibližně 1,1 m/s.
Nápověda 1 – k části b)
Uvědomte si, co (kterou veličinu) vlastně chceme určit?
Řešení nápovědy 1 – k části b)
Chceme určit hmotnost ropy, která za 15 minut vyteče otvorem.
Nápověda 2 – k části b)
Jak určíme hmotnost ropy, která vyteče otvorem v potrubí za 15 minut?
Řešení nápovědy 2 – k části b)
Tuto hmotnost určíme jako:
\[m\,=\,{\rho}{\cdot}V\,,\tag{6}\]
kde ρ je hustota ropy (z tabulek ρ = 840 kg/m³) a V je objem ropy, která vyteče otvorem v potrubí za 15 minut.
Nápověda 3 – k části b)
Abychom mohli určit hmotnost m podle vztahu (6), potřebujeme znát objem V ropy, která vyteče otvorem v potrubí za 15 minut. Jak tento objem zjistíme? Zjistěte objem V a pomocí něho hmotnost vyteklé ropy.
Řešení nápovědy 3 – k části b)
Tento objem jsme již zjistili v nápovědě 6 předchozí části a). Máme nyní všechny potřebné informace ke zjištění hmotnosti ropy, která vyteče při havárii. Dosazením číselných hodnot do (6) dostáváme:
\[m\,=\,840{\cdot}377{,}5\,\mathrm{kg}\,=\,317\,100\,\mathrm{kg}\,\dot=\,317\,\mathrm{t}\,.\]
Během havárie vyteče otvorem v potrubí asi 317 tun ropy.
Nápověda 1 – k části c)
Jaký je objem ropy, která by se použila k výrobě benzinu?
Řešení nápovědy 1 – k části c)
Je to objem ropy vyteklé při havárii, tedy 377,5 m³ ropy (viz část a), nápověda 6).
Nápověda 2 – k části c)
Kolik by se z vyteklé ropy dalo vyrobit benzinu? Vypočtěte tento objem a převeďte výsledek na litry.
Řešení nápovědy 2 – k části c)
Z vyteklé ropy by se dalo vyrobit poloviční množství benzinu. Tento objem označíme V_B a platí:
\[V_\mathrm{B}\,=\,\frac{V}{2}\,=\,188{,}75\,\mathrm{m}^3\,=\,188\,750\,\mathrm{dm}^3\,=\,188\,750\,\mathrm {l}\,.\]
Nápověda 3 – k části c)
Kolik automobilových nádrží by se tímto objemem benzinu mohlo naplnit?
Řešení nápovědy 3 – k části c)
Označme počet naplněných nádrží n. Pak platí:
\[n\,=\,\frac{V_\mathrm{B}}{V_1},\tag{7}\]
kde V_B je celkový objem benzinu a V₁ je objem jedné automobilové nádrže. Číselně:
\[n\,=\,\frac{188 750}{55}\,\dot=\,3431 \,.\]
(Pozor, uvažujeme celé číslo, protože nás zajímají celé naplněné nádrže, nezaokrouhlujeme nahoru, ale dolů.) Uniklá ropa by stačila na naplnění 3431 automobilových nádrží benzinem.
Nápověda 1 – k části d)
Postupujeme podobně jako v části b). V čem bude jediný rozdíl?
Řešení nápovědy 1 – k části d)
Nyní nás zajímá, kolik ropy proteče za rok. Je tedy rozdíl v časovém úseku, pro který počítáme.
Nápověda 2 – k části d)
Jak se změní objem V ropy, která se přepraví za rok, a tudíž i hmotnost ropy, která se přepraví?
Řešení nápovědy 2 – k části d)
Objem (i hmotnost) přepravené ropy bude větší. A bude tolikrát větší, kolikrát je rok převedený na minuty delší než 15 minut.
Nápověda 3 – k části d)
Kolikrát je rok převedený na minuty delší než 15 minut? (Uvažujeme, že rok má 365 dní.)
Řešení nápovědy 3 – k části d)
Jedna hodina je čtyřikrát delší než 15 minut. Den má 24 hodin a rok má 365 dní. Jestliže označíme, že rok převedený na minuty je x-krát delší než 15 minut, máme:
\[x\,=\,4{\cdot}24{\cdot}365\,=\,35040\,.\tag{8}\]
Nápověda 4 – k části d)
S využitím vztahu (6) v části b) dopočítejte hmotnost ropy přepravené za rok.
Řešení nápovědy 4 – k části d)
Po dosazení:
\[m\,=\,({840{\cdot}377{,}5{\cdot}35040})\,\mathrm{kg}\,=\,11\,111\,184\,000\,\mathrm{kg}\,,\] \[m\,=\,11\,111\,184\,\mathrm{t}\,.\]
Za jeden rok se ropovodem přepraví 11 111 184 tun ropy.
Celkové řešení
Řešení části a):
Ropa, která proteče trubkou za 15 minut, tvoří válec. Tento válec má obsah podstavy rovný průřezu trubky S. Výška válce je rovna dráze s, kterou ropa (vybraný atom nebo část ropy) urazí za daný čas, tedy 15 minut.

Objem takového válce určíme podle vzorce:
\[V\,=\,S{\cdot}s\,,\tag{1}\]
kde S je průřez trubky ropovodu (resp. jeho obsah) a s je vzdálenost, o kterou se ropa posune za 15 minut.

Tuto vzdálenost umíme určit, když uvážíme, že ropa se pohybuje rovnoměrným pohybem (rychlost se nemění, je stálá). Pro dráhu rovnoměrného pohybu platí:
\[s\,=\,v{\cdot}t\,,\tag{2}\]
kde v je rychlost tohoto pohybu a t doba pohybu (v našem případě 15 min).

Dosazením (2) do (1) získáme:
\[V\,=\,S {\cdot} v{\cdot} t\,,\tag{3}\]
kde S je průřez trubky ropovodu (resp. jeho obsah), v je rychlost, kterou ropa teče, a t doba pohybu ropy (v našem případě 15 min).

Vyjádříme neznámou rychlost v:
\[v\,=\,\frac {V}{S{\cdot} t}\,,\tag{4}\]
kde V je objem ropy, která proteče ropovodem za 15 minut, S je průřez trubky ropovodu (resp. jeho obsah) a t doba pohybu ropy (v našem případě 15 min).

Potřebujeme ještě zjistit obsah průřezu trubky S a objem V – jaký objem ropy proteče ropovodem za 15 minut.

Objem V určíme trojčlenkou:

za 60 minut……………1510 m³ ropy

za 15 minut……………V m³ ropy
------------------------------------------------------
\(\frac{V}{1510}\,=\,\frac{15}{60}\,,\)

tedy \(V\,=\,\frac{1510{\cdot}15}{60}\,\,\mathrm{m}^3\,=\,377{,}5\,\mathrm{m}^3\,.\)

Za 15 minut proteče ropovodem 377,5 m³ ropy.

Známe poloměr trubky r, takže můžeme vypočítat obsah průřezu jako obsah kruhu s poloměrem r:
\[S\,=\,{\pi}r^2\,.\tag{5}\]
Číselně:
\[S\,=\,{\pi}{\cdot}(0{,}35)^2\,\mathrm{m}^2\,\dot=\,0{,}38\,\mathrm{m}^2\,.\]
Rychlost ropy spočítáme dosazením do vzorce (4). Číselně:
\[v\,=\,\frac{V}{S{\cdot}t}\,=\,\frac{377{,}5}{0{,}38{\cdot}15{\cdot}60} \,\mathrm{m\cdot s^{-1}}\,\dot=\,1{,}1\,\mathrm{m\cdot s^{-1}}\,.\]

Řešení části b):
Nyní chceme určit hmotnost ropy, která za 15 minut vyteče otvorem.

Tuto hmotnost určíme jako:
\[m\,=\,{\rho}{\cdot}V\,,\tag{6}\]
kde ρ je hustota ropy (z tabulek ρ = 840 kg/m³) a V je objem ropy, která vyteče otvorem v potrubí za 15 minut.

Tento objem jsme již zjistili v předchozí části a). Stačí dosadit číselné hodnoty do (6) a dostáváme:
\[m\,=\,840{\cdot}377{,}5\,\mathrm{kg}\,=\,317\,100\,\mathrm{kg}\,\dot=\,317\,\mathrm{t}\,.\]

Řešení části c):
Nejprve potřebujeme určit objem ropy použité k výrobě benzinu. Je to objem ropy vyteklé při havárii, tedy 377,5 m³ ropy (viz část a).

Víme, že z vyteklé ropy by se dalo vyrobit poloviční množství benzinu. Tento objem označíme V_B a platí:
\[V_\mathrm{B}\,=\,\frac{V}{2}\,=\,188{,}75\,\mathrm{m}^3\,=\,188\,750\,\mathrm{dm}^3\,=\,188\,750\,\mathrm{l}\,.\]
Počet automobilových nádrží, které by šlo vyrobeným benzinem naplnit, označíme n. Platí:
\[n\,=\,\frac{V_\mathrm{B}}{V_1}\,,\tag{7}\]
kde V_B je celkový objem benzinu a V₁ je objem jedné automobilové nádrže. Číselně:
\[n\,=\,\frac{188 750}{55}\,\dot=\,3431 \,.\]
(Pozor, uvažujeme celé číslo, protože nás zajímají celé naplněné nádrže, nezaokrouhlujeme nahoru, ale dolů.)

Řešení části d):

Postupujeme podobně jako v části b). Jediný rozdíl je v časovém úseku, pro který počítáme. Nyní nás zajímá, kolik ropy proteče za rok.

Objem (i hmotnost) přepravené ropy budou tolikrát větší, kolikrát je rok převedený na minuty delší než 15 minut.

Jedna hodina je čtyřikrát delší než 15 minut. Den má 24 hodin a rok má 365 dní. Jestliže označíme, že rok převedený na minuty je x-krát delší než 15 minut, máme:
\[x\,=\,4{\cdot}24{\cdot}365\,=\,35040\,.\tag{8}\]
S využitím vztahu (6) v části b) a po dosazení:
\[m\,=\,({840{\cdot}377{,}5{\cdot}35040})\,\mathrm{kg}\,=\,11\,111\,184\,000\,\mathrm{kg}\,,\] \[m\,=\,11\,111\,184\,\mathrm{t}\,.\]
Odpověď
a) Ropa teče ropovodem rychlostí přibližně 1,1 m/s.

b) Během havárie by otvorem uniklo asi 317 tun ropy.

c) Ropa uniklá při havárii by stačila k naplnění 3431 automobilových nádrží.

d) Za jeden rok se ropovodem přepraví 11 111 184 tun ropy.

Úroveň náročnosti: Úloha vhodná pro žáky základní školy

×Původní zdroj: sbírka Petra Nekoly, ZŠ Plzeň