Želva

Úloha číslo: 828

V akváriu plave ostrůvek a na něm odpočívá vodní želva. Jak se změní výška hladiny vody v akváriu, jestliže želva opustí ostrůvek, potopí se a na dně akvária bude opět odpočívat?

Nápověda 1
Jaké síly působí na ostrůvek v obou případech? Nakreslete je do obrázku.
Řešení nápovědy 1
První případ

Druhý případ

Na obrázcích vidíme, že v obou případech působí na ostrůvek tíhová síla (F_o) a vztlaková síla vody (F_vz). V prvním případě působí na ostrůvek ještě želva svou tíhou (F_z).
Nápověda 2
Ostrůvek je v obou případech v rovnováze. Co z toho můžeme vyvodit z hlediska působících sil?
Řešení nápovědy 2
Výsledná síla působící na ostrůvek je nulová.

V prvním případě platí:
\[F_\mathrm{o}+F_\mathrm{z}=F_\mathrm{vz1}.\tag{1}\]
Ve druhém případě platí:
\[F_\mathrm{o}=F_\mathrm{vz2}.\tag{2}\]
Nápověda 3
Jak vypočítáme velikost tíhové síly působící na ostrůvek, vztlakové síly vody a tíhu želvy?
Řešení nápovědy 3
Pro tíhovou sílu působící na ostrůvek F_o platí vztah:
\[F_\mathrm{o}=m_\mathrm{o}g\,,\tag{3}\]
kde m_o je hmotnost ostrůvku a g je tíhové zrychlení.

Pro tíhu želvy F_z platí vztah:
\[F_\mathrm{z}=m_\mathrm{z}g\,,\tag{4}\]
kde m_z je hmotnost želvy.

Pro vztlakovou sílu F_vz platí vztah:
\[ F_\mathrm{vz}=V_\mathrm{pct}\rho_\mathrm{kap}g\,,\]
kde V_pct je objem ponořené části tělesa a ρ_kap je hustota kapaliny.

První případ

Pro vztlakovou sílu v prvním případě F_vz₁ bude \(V_\mathrm{pct}=V_{1}\) a \(\rho_\mathrm{kap}=\rho_\mathrm{H_{2}O}\), kde V₁ je objem, který vytlačil ostrůvek s želvou, a ρ_H₂O je hustota vody. Platí tedy vztah:
\[F_\mathrm{vz_{1}}=V_{1}\rho_\mathrm{H_{2}O}g\,.\tag{5}\]

Druhý případ

Pro vztlakovou sílu ve druhém případě F_vz₂ bude \(V_\mathrm{pct}=V_{2}\) a \(\rho_\mathrm{kap}=\rho_\mathrm{H_{2}O}\), kde V₂ je objem, který vytlačil ostrůvek. Platí tedy vztah:
\[F_\mathrm{vz_{2}}=V_{2}\rho_\mathrm{H_{2}O}g\,.\tag{6}\]
Nápověda 4
Dosaďte do vztahů (1), (2) a vyjádřete, jaký objem vytlačí ostrůvek a želva v prvním a ve druhém případě.
Řešení nápovědy 4
První případ

Pro ostrůvek se želvou se dle (1) součet tíhové síly působící na ostrůvek a tíhy želvy rovná vztlakové síle:
\[F_\mathrm{o}+F_\mathrm{z}=F_\mathrm{vz1}.\]
Dle (3), (4) a (5) dostáváme:
\[m_\mathrm{o}g+m_\mathrm{z}g=V_{1}\rho_\mathrm{H_{2}O}g\,.\]
g vykrátíme a obě strany rovnice upravíme tak, že je vydělíme ρ_H₂O, a tím získáme V₁:
\[V_{1}=\frac{m_\mathrm{o}+m_\mathrm{z}}{\rho_\mathrm{H_{2}O}}.\tag{7}\]

Druhý případ

Pro ostrůvek se dle (2) velikost tíhové síly působící na ostrůvek rovná vztlakové síle:
\[F_\mathrm{o}=F_\mathrm{vz_{2}}.\]
Dle (3) a (6) dostáváme:
\[m_\mathrm{o}g=V_{2}\rho_\mathrm{H_{2}O}g\,.\]
g vykrátíme a obě strany rovnice upravíme tak, že je vydělíme ρ_H₂O, a tím získáme V₂:
\[V_{2}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}}.\tag{8}\]

Želva vytlačí objem V₃:
\[V_{3}=\frac{m_\mathrm{z}}{\rho_\mathrm{z}}\,,\tag{9}\]
kde ρ_z je hustota želvy.

Celkově vytlačí ostrůvek a želva objem V_c, pro který platí:
\[V_\mathrm{c}=V_{2}+V_{3}\,.\]
Dle (8) a (9) dostáváme:
\[V_\mathrm{c}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}}+\frac{m_\mathrm{z}}{\rho_\mathrm{z}}\,.\tag{10}\]
Nápověda 5
Porovnejte celkový vytlačený objem v prvním (7) a ve druhém případě (10).
Řešení nápovědy 5
\[V_{1}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}} + \frac{m_\mathrm{z}}{\rho_\mathrm{H_{2}O}}\] \[V_\mathrm{c}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}}+\frac{m_\mathrm{z}}{\rho_\mathrm{z}}\]
Hustota želvy je větší než hustota vody \(\rho_\mathrm{z}\gt\rho_\mathrm{H_{2}O}\).

Ve vzorci (10) je pak člen \(\frac{m_\mathrm{z}}{\rho_\mathrm{z}}\) menší než člen \(\frac{m_{z}}{\rho_\mathrm{H_{2}O}}\) ve vztahu (7).

Proto je \(V_\mathrm{c}\lt\ V_{1}\) a z toho důvodu hladina vody klesne.
Poznámka
Experimentálně zjištěná hustota vodní želvy chované na gymnáziu Špitálská je 1100 kg·m^-3. Její hustota se od hustoty vody příliš neliší, proto pokles hladiny nebude moc patrný.

Pokud nemáte vodní želvu na ostrůvku, můžete je nahradit kamenem a miskou od Termixu. Místo akvária použijte misku s vodou.
Celkové řešení
Nakreslíme síly působící na ostrůvek v obou případech.

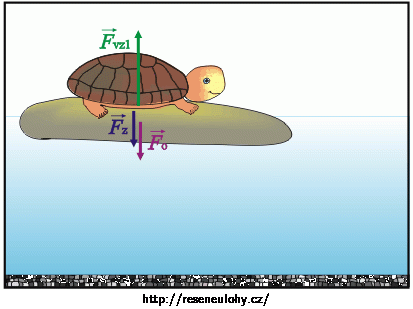
První případ

Druhý případ

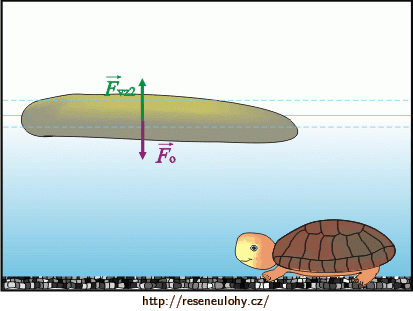
Na obrázcích vidíme, že v obou případech působí na ostrůvek tíhová síla (F_o) a vztlaková síla vody (F_vz). V prvním případě působí na ostrůvek ještě želva svou tíhou (F_z).

Ostrůvek je v obou případech v rovnováze, proto je výsledná síla působící na ostrůvek nulová. Z toho důvodu budou platit následující vztahy.

V prvním případě:
\[F_\mathrm{o}+F_\mathrm{z}=F_\mathrm{vz1}\,.\tag{1}\]
Ve druhém případě:
\[F_\mathrm{o}=F_\mathrm{vz2}\,.\tag{2}\]

Vyjádření tíhové síly působící na ostrůvek, vztlakové síly vody a tíhy želvy:

Pro tíhovou sílu působící na ostrůvek F_o platí vztah:
\[F_\mathrm{o}=m_\mathrm{o}g\,,\tag{3}\]
kde m_o je hmotnost ostrůvku a g je tíhové zrychlení.

Pro tíhu želvy F_z platí vztah:
\[F_\mathrm{z}=m_\mathrm{z}g\,,\tag{4}\]
kde m_z je hmotnost želvy.

Pro vztlakovou sílu F_vz platí vztah:
\[ F_\mathrm{vz} =V_\mathrm{pct}\rho_\mathrm{kap}g\,,\]
kde V_pct je objem ponořené části tělesa a ρ_kap je hustota kapaliny.

První případ

Pro vztlakovou sílu v prvním případě F_vz₁ bude \(V_\mathrm{pct}=V_{1}\) a \(\rho_\mathrm{kap}=\rho_\mathrm{H_{2}O}\), kde V₁ je objem, který vytlačil ostrůvek s želvou, a ρ _H₂O je hustota vody. Platí tedy vztah:
\[F_\mathrm{vz_{1}}=V_{1}\rho_\mathrm{H_{2}O}g\,.\tag{5}\]

Druhý případ

Pro vztlakovou sílu ve druhém případě F_vz₂ bude \(V_\mathrm{pct}=V_{2}\) a \(\rho_\mathrm{kap}=\rho_\mathrm{H_{2}O}\), kde V₂ je objem, který vytlačil ostrůvek. Platí tedy vztah:
\[F_\mathrm{vz_{2}}=V_{2}\rho_\mathrm{H_{2}O}g\,.\tag{6}\]

Objem vytlačený ostrůvkem a želvou:

První případ

Pro ostrůvek se želvou se dle (1) součet tíhové síly působící na ostrůvek a tíhy želvy rovná vztlakové síle:
\[F_\mathrm{o}+F_\mathrm{z}=F_\mathrm{vz1}.\]
Dle (3), (4) a (5) dostáváme:
\[m_\mathrm{o}g+m_\mathrm{z}g=V_{1}\rho_\mathrm{H_{2}O}g\,.\]
g vykrátíme a obě strany rovnice upravíme tak, že je vydělíme ρ_H₂O a tím získáme V₁.
\[V_{1}=\frac{m_{o}+m_{z}}{\rho_{H_{2}O}}\tag{7}\]

Druhý případ

Pro ostrůvek se dle (2) velikost tíhové síly působící na ostrůvek rovná vztlakové síle.
\[F_\mathrm{o}=F_\mathrm{vz_{2}}\]
Dle (3) a (6) dostáváme:
\[m_\mathrm{o}g=V_{2}\rho_\mathrm{H_{2}O}g\,.\]
g vykrátíme a obě strany rovnice upravíme tak, že je vydělíme ρ_H₂O, a tím získáme V₂:
\[V_{2}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}}.\tag{8}\]

Želva vytlačí objem V₃:
\[V_{3}=\frac{m_\mathrm{z}}{\rho_\mathrm{z}},\tag{9}\]
kde ρ_z je hustota želvy.

Celkově vytlačí ostrůvek a želva objem V_c, pro který platí:
\[V_\mathrm{c}=V_{2}+V_{3}\,.\]
Dle (8) a (9) dostáváme:
\[V_\mathrm{c}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}}+\frac{m_\mathrm{z}}{\rho_\mathrm{z}}\,.\tag{10}\]

Porovnání celkového vytlačeného objemu v prvním a ve druhém případě:

Porovnáme vztah (7) se vztahem (10):
\[V_{1}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}} + \frac{m_\mathrm{z}}{\rho_\mathrm{H_{2}O}}\] \[V_\mathrm{c}=\frac{m_\mathrm{o}}{\rho_\mathrm{H_{2}O}}+\frac{m_\mathrm{z}}{\rho_\mathrm{z}}\]
Hustota želvy je větší než hustota vody \(\rho_\mathrm{z}\gt\rho_\mathrm{H_{2}O}\,.\)

Ve vzorci (10) je pak člen \(\frac{m_\mathrm{z}}{\rho_\mathrm{z}}\) menší než člen \(\frac{m_\mathrm{z}}{\rho_\mathrm{H_{2}O}}\) ve vztahu (7).

Proto je \(V_\mathrm{c}\lt\ V_{1}\) a z toho důvodu hladina vody klesne.
Odpověď
Objem, který vytlačí želva a ostrůvek ve druhém případě, je menší než v prvním případě, proto hladina vody klesne.