Sáňky na zasněženém svahu
Úloha číslo: 139
Chlapec táhne sáňky vzhůru po zasněženém svahu se stoupáním β za provázek, který svírá s rovinou svahu úhel α. Najděte takovou velikost úhlu α, při kterém bude síla vynaložená na tažení saní nejmenší. Koeficient smykového tření mezi saněmi a sněhem je f = 0,1 a rychlost saní zůstává stálá.

Zápis
f = 0,1 koeficient tření mezi sáněmi a sněhem β sklon svahu α = ? odchylka provázku saní a svahu, při níž bude síla vynaložená na tažení saní nejmenší Rozbor

Máme určit, při jakém úhlu α, který svírá provázek se svahem, bude síla vynaložená na tažení saní minimální.
Nejprve musíme zjistit, jak tato síla závisí na úhlu α (T = T(α)).
Víme také, že sáně jedou stálou rychlostí. Uvědomte si, co z toho vyplývá pro zrychlení saní.
Při vyjádření třecí síly je také třeba mít na paměti, že provázek není rovnoběžný se svahem, ale svírá s ním úhel α, což ovlivňuje velikost síly, kterou sáně tlačí na svah.
Nápověda 1 – síly působící na sáňky, pohybová rovnice, zrychlení saní
Nakreslete si obrázek a vyznačte v něm všechny síly, které působí na sáňky. Napište pro sáňky pohybovou rovnici. Uvědomte si, jaké je zrychlení saní, když je rychlost saní konstantní.
Nápověda 2 – pohybová rovnice skalárně
Pohybovou rovnici je třeba zapsat skalárně. Zvolte vhodně souřadný systém, najděte průměty sil do příslušných směrů a přepište v těchto směrech pohybovou rovnici.
Nápověda 3 – vyjádření třecí síly
Uvědomte si, na čem závisí velikost třecí síly a jak se dá vyjádřit vztah pro její výpočet.
Nápověda 4 – vyjádření tahové síly
Dosaďte do rovnice (2) třecí sílu a vyjádřete z ní tahovou sílu T.
Nápověda 5 – výpočet úhlu alfa
Hledáte takový úhel α, aby tahová síla byla minimální. Hledáte tedy minimum funkce \[T(\alpha)\,=\,\frac{F_\mathrm{G}(\sin\beta\,+\,f\cos\beta)}{f\sin\alpha\,+\,\cos\alpha},\] kde T(α) znamená funkci T s proměnnou α. Minimum funkce T(α) najdete pomocí derivace této funkce podle proměnné α.
CELKOVÉ ŘEŠENÍ
Do obrázku nakreslíme všechny síly působící na sáňky a napíšeme pro ně pohybovou rovnici.
Síly působící na sáňky:
\(\vec{F}_\mathrm{G}\)…síla tíhová,
\(\vec{N}\)…síla, kterou tlačí svah na sáňe,
\(\vec{T}\)…tahová síla, kterou chlapec táhne sáňky po svahu,
\(\vec{F}_\mathrm{t}\)…síla třecí, která určuje, jak se sáňky „brzdí“ o svah.
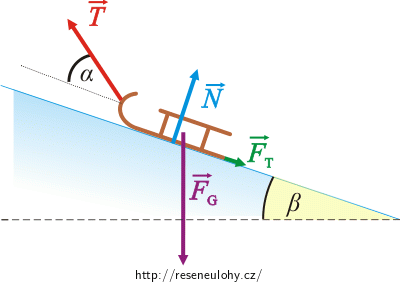
Pohybová rovnice pro sáňky:
\[ \vec{F}_\mathrm{G}+ \vec{N} + \vec{T} + \vec{F}_\mathrm{t} = m\vec{a} = 0. \tag{1}\]m…hmotnost saní
\(\vec{a}\)…zrychlení saní
Zrychlení saní:
Protože rychlost \(\vec{v}\) je konstantní, je zrychlení \(\vec{a}\) nulové a výslednice sil působících na sáně je tedy nulová.
Abychom mohli pohybovou rovnici přepsat skalárně, zvolíme si souřadný systém os x, y tak, že osu x zvolíme ve směru pohybu sáněk. Osa y je na osu x kolmá.
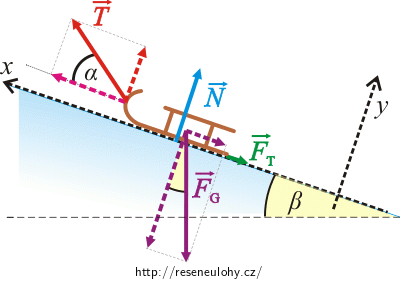
Tíhovou sílu \(\vec{F}_\mathrm{G}\) a tahovou sílu \(\vec{T}\) rozložíme na 2 složky do směru těchto os:
\[F_\mathrm{Gx}\,=\,F_\mathrm{G}\sin\beta,\] \[F_\mathrm{Gy}\,=\,F_\mathrm{G}\cos\beta,\] \[T_\mathrm{x}\,=\,T\cos\alpha,\] \[T_\mathrm{y}\,=\,T\sin\alpha.\]Průmět do osy x:
\[ T\cos\alpha \,-\, F_\mathrm{G}\sin\beta \,-\,F_\mathrm{t} \,=\, 0. \tag{2}\]Průmět do osy y:
\[ T\sin\alpha \,+\, N \,-\, F_\mathrm{G}\cos\beta \,=\, 0. \tag{3}\]Třecí síla:
Třecí síla působící na sáňky je úměrná tlakové síle, kterou sáňky působí na svah. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí svah na sáňky. Zapíšeme to rovnicí:
\[F_\mathrm{t}\,=\,fN.\]Sílu N vyjádříme z rovnice (3):
\[N\,=\,F_\mathrm{G}\cos\beta\,-\,T\sin\alpha.\]Pro třecí sílu platí:
\[F_\mathrm{t}\,=\,f\left(F_\mathrm{G}\cos\beta\,-\,T\sin\alpha\right).\tag{4}\]Výpočet tahové síly:
Do rovnice (2) dosadíme za třecí sílu vztah (4) a upravíme:
\[T\cos\alpha \,-\, F_\mathrm{G}\sin\beta \,-\, f\left(F_\mathrm{G}\cos\beta\,-\,T\sin\alpha\right)\,=\, 0, \] \[T\cos\alpha \,-\, F_\mathrm{G}\sin\beta \,+\,f T\sin\alpha \,-\, fF_\mathrm{G}\cos\beta= 0,\] \[T\cos\alpha\,+\,f T\sin\alpha\,=\,F_\mathrm{G}\sin\beta\,+\,fF_\mathrm{G}\cos\beta,\] \[T\left(f\sin\alpha\,+\,\,\cos\alpha\right)\,=\,F_\mathrm{G}\left(\sin\beta\,+\,f\cos\beta\right),\] \[T\,=\,\frac{F_\mathrm{G}(\sin\beta\,+\,f\cos\beta)}{f\sin\alpha\,+\,\cos\alpha}.\tag{5}\]Funkce T(α) nám ukazuje, jak se mění síla T s proměnnou α. Minimum funkce T(α) najdeme tak, že ji zderivujeme podle proměnné α a tuto derivaci položíme rovnu nule. Abychom ověřili, že jde opravdu o minimum funkce a nikoliv maximum, je třeba ještě zjistit, zda platí, že druhá derivace funkce T(α) podle α je v daném bodě větší než nula.
\[\frac{\mathrm{d}T}{\mathrm{d}\alpha}= \frac{\mathrm{d}}{\mathrm{d}\alpha}\left[\frac{F_\mathrm{G}(\sin\beta+f\cos\beta)}{f\sin\alpha+\cos\alpha}\right],\] \[\frac{\mathrm{d}T}{\mathrm{d}\alpha}= F_\mathrm{G}\left(\sin\beta+f\cos\beta\right)\frac{\mathrm{d}}{\mathrm{d}\alpha}\left(\frac{1}{f\sin\alpha+\cos\alpha}\right),\] \[\frac{\mathrm{d}T}{\mathrm{d}\alpha}= F_\mathrm{G}(\sin\beta+f\cos\beta)\frac{-(f\cos\alpha-\sin\alpha)} {(f\sin\alpha+\cos\alpha)^2}.\]Aby se tato rovnice rovnala nule, musí se čitatel na pravé straně rovnice rovnat nule. Člen FG(sinβ + fcosβ) ≠ 0, musí se tedy rovnat nule člen (fcosα − sinα). Z této podmínky získáme velikost úhlu alfa:
\[-f\cos\alpha+\sin\alpha=0,\] \[\sin\alpha=f\cos\alpha,\] \[\mathrm{tg}\alpha=f,\] \[\alpha=\mathrm{arctg} f.\tag{6}\]Do vztahu (6) dosadíme číselně:
\[\alpha=\mathrm{arctg} 0{,}1=5^{\circ}43^\prime.\]Ověření, že jde o minimum funkce:
\[\frac{\mathrm{d}^2T}{\mathrm{d}\alpha^2}= -F_\mathrm{G}\left(\sin\beta+f\cos\beta\right)\frac{\mathrm{d}}{\mathrm{d}\alpha}\left[\frac{f\cos\alpha-\sin\alpha} {(f\sin\alpha+\cos\alpha)^2}\right],\] \[\frac{\mathrm{d}^2T}{\mathrm{d}\alpha^2}=-F_\mathrm{G}(\sin\beta+f\cos\beta)\] \[\frac{(-f\sin\alpha-\cos\alpha)(f\sin\alpha+\cos\alpha)^2- 2(f\sin\alpha+\cos\alpha)(f\cos\alpha-\sin\alpha)^2} {(f\sin\alpha+\cos\alpha)^4},\] \[\frac{\mathrm{d}^2T}{\mathrm{d}\alpha^2}=-F_\mathrm{G}(\sin\beta+f\cos\beta)\] \[\frac{-(f\sin\alpha+\cos\alpha)^3-2(f\sin\alpha+\cos\alpha)(f\cos\alpha-\sin\alpha)^2} {(f\sin\alpha+\cos\alpha)^4},\] \[\frac{d^2T}{d\alpha^2}=F_\mathrm{G}(\sin\beta+f\cos\beta) \frac{(f\sin\alpha+\cos\alpha)^2+2(f\cos\alpha-\sin\alpha)^2} {(f\sin\alpha+\cos\alpha)^3}\gt 0.\]Úhly α i β jsou menší než 90°, takže siny i cosiny těchto úhlů jsou větší než nula.
CELKOVÁ ODPOVĚĎ
Velikost úhlu α, při kterém bude síla vynaložená na tažení saní nejmenší, je rovna \[\alpha=\mathrm{arctg} f=5^{\circ}43^\prime.\]





