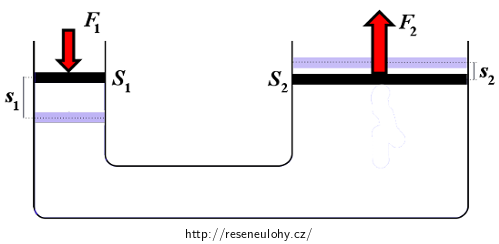
Hydraulický lis

Úloha číslo: 1001

Obsahy průřezů válců hydraulického lisu jsou 20 cm² a 800 cm². Na menší píst působí síla o velikosti 100 N. Určete:

Tlak, který tato síla vyvolá v kapalině.
Velikost tlakové síly působící na větší píst.
Dráhu, o kterou se posune větší píst, jestliže se menší píst posune o 8 cm.
Práci, kterou při tomto posunutí vykoná tlaková síla.

Zápis

S₁ = 20 cm² = 2·10⁻³ m²	obsah plochy průřezu menšího válce
S₂ = 800 cm² = 8·10⁻² m²	obsah plochy průřezu většího válce
F₁ = 100 N	síla působící na menší píst
s₁ = 8 cm = 8·10⁻² m	posunutí menšího pístu
p = ?	tlak vyvolaný silou F₁ v kapalině
F₂ = ?	tlaková síla na větší píst
s₂ = ?	posunutí většího pístu
W = ?	práce vykonaná tlakovou silou

Nápověda 1 (k části a.)
Jak je definován tlak? K výpočtu využijte definičního vztahu.
Řešení nápovědy 1
Tlak p je definován jako podíl síly F, která působí kolmo na plochu o obsahu S (není-li jinak uvedeno, obvykle předpokládáme právě kolmé působení síly na plochu). V našem případě jde o sílu F₁ a obsah plochy menšího pístu S₁, tedy:
\[p\,=\,\frac{F_1}{S_1}\,=\,\frac{100}{2{\cdot}10^{-3}}\,\mathrm{Pa}\,=\,50\,\mathrm{kPa}\,.\]
Nápověda 2 (k části b.)
Tlak v kapalině, určený v předchozím výpočtu, je způsoben vnější silou F₁. Znáte poučku, která říká, jak je to s velikostí tlaku způsobeného vnější silou v různých částech objemu kapaliny?
Řešení nápovědy 2
Podle tzv. Pascalova zákona je tlak vyvolaný vnější silou ve všech místech kapaliny stejný.
Nápověda 3 (k části b.)
Pomocí Pascalova zákona a definice tlaku určete tlakovou sílu F₂ (předpokládáme, že také ona má směr kolmý k ploše pístu).
Řešení nápovědy 3
Jestliže je podle Pascalova zákona tlak v kapalině vyvolaný vnější silou ve všech jejích místech stejný, lze jej vyjádřit nejen jako v části a., ale také pomocí plochy velkého pístu a síly na ni působící:
\[p\,=\,\frac{F_1}{S_1}\,=\,\frac{F_2}{S_2}\,.\]
Odtud vyjádříme a číselně dopočítáme tlakovou sílu F₂:
\[F_2\,=\,F_1\frac{S_2}{S_1}\,=\,100\,\frac{8{\cdot}10^{-2}}{2{\cdot}10^{-3}}\,\mathrm{N}\,=\,4\,\mathrm{kN}\,.\]
Nápověda 4 (k části c.)
Jakou vlastnost kapalin vlastně hydraulický lis při své práci využívá? Kterou fyzikální veličinu kapaliny (na rozdíl třeba od plynů) při mechanických dějích nemění?
Řešení nápovědy 4
V případě hydraulického lisu využíváme fakt, že kapaliny jsou prakticky nestlačitelné (uvažujeme dokonce ideální nestlačitelnost). Kapaliny si tedy zachovávají svůj objem. (Neuvažujeme teplotní roztažnost apod.)
Nápověda 5 (k části c.)
O jaký objem se zmenší prostor pro kapalinu ve válci s menším pístem, posuneme-li ho o dráhu s₁ (směrem „do kapaliny“)? Stejný objem se zjevně musí (vzhledem k nestlačitelnosti kapalin) „uprázdnit“ ve válci s větším pístem – odtud určete posunutí většího válce.
Řešení nápovědy 5
Posunutím menšího pístu s obsahem plochy S₁ o dráhu s₁ (směrem „do kapaliny“) se ve válci s tímto pístem zmenší objem kapaliny o ΔV.

O stejný objem se musí zvětšit objem kapaliny ve válci s velkým pístem, který má plochu S₂ a posune se o dráhu s₂.

Objem ΔV určíme v obou případech jako objem válce, vynásobíme tedy obsah podstavy „výškou“, tj. posunutím:
\[{\Delta}V\,=\,S_1s_1\,=\,S_2s_2\,.\]
Odtud vyjádříme posunutí s₂ jako:
\[s_2\,=\,s_1\,\frac{S_1}{S_2}\,.\]
Číselně:
\[s_2\,=\,8{\cdot}10^{-2}{\cdot}\,\frac{2{\cdot}10^{-3}}{8{\cdot}10^{-2}}\,\mathrm{m}\,=\,2\,\mathrm{mm}\,.\]
Nápověda 6 (k části d.)
Vyjděte z definice mechanické práce. Je podstatné, zda budeme počítat práci tlakových sil na menší nebo na větší píst?
Řešení nápovědy 6
V případě, že je působící síla konstantní a působí ve směru posunutí, můžeme mechanickou práci spočítat jako součin této konstantní síly F a posunutí s. V našem případě tedy půjde o posunutí malého pístu silou F₁ o dráhu s₁ nebo o posunutí velkého pístu silou F₂ o dráhu s₂. Výpočtem lze ukázat, že vykonaná práce je v obou případech stejná. Tedy:
\[W\,=\,F_1s_1\,=\,100{\cdot}8{\cdot}10^{-2}\,\mathrm{J}\,=\,8\,\mathrm{J}\,.\] A také: \[W\,=\,F_2s_2\,=\,4000{\cdot}2{\cdot}10^{-3}\,\mathrm{J}\,=\,8\,\mathrm{J}\,.\]
Celkové řešení
Část a.:
Tlak p je definován jako podíl síly F, která působí kolmo na plochu o obsahu S (není-li jinak uvedeno, obvykle předpokládáme právě kolmé působení síly na plochu). V našem případě jde o sílu F₁ a obsah plochy menšího pístu S₁, tedy:
\[p\,=\,\frac{F_1}{S_1}\,=\,\frac{100}{2{\cdot}10^{-3}}\,\mathrm{Pa}\,=\,50\,\mathrm{kPa}\,.\]
Část b.:
Výše určený tlak v kapalině je způsoben vnější silou o velikosti F₁. Podle Pascalova zákona je tlak vyvolaný vnější silou ve všech místech kapaliny stejný. Lze jej tedy vyjádřit nejen jako v části a., ale také pomocí plochy velkého pístu a síly na ni působící:
\[p\,=\,\frac{F_1}{S_1}\,=\,\frac{F_2}{S_2}\,.\]
Odtud vyjádříme a číselně dopočítáme tlakovou sílu F₂:
\[F_2\,=\,F_1\frac{S_2}{S_1}\,=\,100\,\frac{8{\cdot}10^{-2}}{2{\cdot}10^{-3}}\,\mathrm{N}\,=\,4\,\mathrm{kN}\,.\]
Část c.:
V případě hydraulického lisu využíváme fakt, že kapaliny jsou prakticky nestlačitelné (uvažujeme dokonce ideální nestlačitelnost) a zachovávají si tedy svůj objem. (Neuvažujeme-li teplotní roztažnost apod.) Posunutím menšího pístu s obsahem plochy S₁ o dráhu s₁ (směrem „do kapaliny“) se ve válci s tímto pístem zmenší objem kapaliny o ΔV.

O stejný objem se musí zvětšit objem kapaliny ve válci s velkým pístem, který má plochu S₂ a posune se o dráhu s₂.

Objem ΔV určíme v obou případech jako objem válce, vynásobíme tedy obsah podstavy „výškou“, tj. posunutím:
\[{\Delta}V\,=\,S_1s_1\,=\,S_2s_2\,.\]
Odtud vyjádříme posunutí s₂ jako:
\[s_2\,=\,s_1\,\frac{S_1}{S_2}\,.\]
Číselně:
\[s_2\,=\,8{\cdot}10^{-2}{\cdot}\,\frac{2{\cdot}10^{-3}}{8{\cdot}10^{-2}}\,\mathrm{m}\,=\,2\,\mathrm{mm}\,.\]
Část d.:
Mechanická práce je v případě konstantní síly působící ve směru posunutí definována jako součin této konstantní síly F a posunutí s. V našem případě tedy půjde o posunutí malého pístu silou F₁ o dráhu s₁ nebo o posunutí velkého pístu silou F₂ o dráhu s₂. Výpočtem lze ukázat, že vykonaná práce je v obou případech stejná. Tedy:
\[W\,=\,F_1s_1\,=\,100{\cdot}8{\cdot}10^{-2}\,\mathrm{J}\,=\,8\,\mathrm{J}\,.\]
A také:
\[W\,=\,F_2s_2\,=\,4000{\cdot}2{\cdot}10^{-3}\,\mathrm{J}\,=\,8\,\mathrm{J}\,.\]
Odpověď
1. Síla o velikosti 100 N vyvolává v kapalině tlak 50 kPa.
2. Na větší píst působí tlaková síla o velikosti 4 kN.
3. Velký píst se posune o 2 mm.
4. Tlaková síla vykoná práci 8 J.