Auto a brzdná síla přímo úměrná rychlosti
Úloha číslo: 70
Auto o hmotnosti 1 000 kg jede rovnoměrně přímočaře rychlostí o velikosti 30 m·s−1 po vodorovné silnici. V čase 0 s proti němu začala působit brzdná síla, která je přímo úměrná rychlosti auta. Konstanta úměrnosti k = 231 kg·s−1.
1) Určete, jak se s časem mění velikost rychlosti auta v(t) a souřadnice auta x(t).
2) Určete, za jak dlouho klesne rychlost auta na poloviční hodnotu, tj. 15 m·s−1.

Poznámka: Místo velikost rychlosti píšeme dále jen rychlost.
Zápis
m = 1 000 kg hmotnost auta v0 = 30 m·s−1 rychlost auta t0 = 0 s čas, ve kterém začala působit brzdná síla Fb brzdná síla úměrná rychlosti auta k = 231 kg·s−1 konstanta úměrnosti t = ? s čas, za který klesne rychlost auta na poloviční hodnotu, tj. 15 m·s−1 Nápověda 1 – pohybová rovnice
Uvědomte si, jaké síly působí na auto, a napište pro něj pohybovou rovnici.
Nápověda 2 – vyjádření brzdné síly, průběh v(t)
Vyjádřete brzdnou sílu Fb z rovnice (2) pomocí rychlosti auta a řeště vzniklou diferenciální rovnici.
Nápověda 3 – průběh x(t)
Znáte závislost rychlosti na čase. Integrací získáte závislost dráhy na čase.
Nápověda 4 – čas pro poloviční hodnotu rychlosti
Hledáte čas, kdy je hodnota rychlosti rovna \(\frac{v_0}{2}\). Přitom víte, jak rychlost na čase závisí.
CELKOVÉ ŘEŠENÍ
Do obrázku nakreslíme síly působící na auto a napíšeme pohybovou rovnici.
Na auto působí následující síly:
\(\vec{F}_\mathrm{b}\)…brzdná síla
\(\vec{F}_\mathrm{G}\)…tíhová síla
\(\vec{N}\)…normálová síla, kterou na auto působí podložka
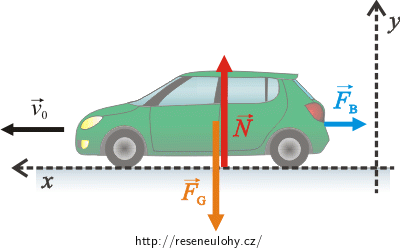
Poznámka: Podložka N působí na kola auta, do obrázku kreslíme výslednici těchto sil.
Pohybová rovnice pro auto je:
\[\vec{F}_\mathrm{b}+\vec{F}_\mathrm{G}+\vec{N}\,=\, m\vec{a}.\tag{1}\]Zvolíme souřadný systém podle obrázku a rovnici (1) přepíšeme skalárně:
\[x:-F_\mathrm{b} \,=\, ma,\tag{2}\] \[y:N - F_\mathrm{G} \,=\, 0.\tag{3}\]Poznámka: Z obrázku můžete vidět, proč je v rovnici (2) znaménko mínus. Brzdná síla působí proti směru pohybu auta. Síly \(\vec{F}_\mathrm{G}\) a \(\vec{N}\) jsou kolmé na brzdnou sílu \(\vec{F}_\mathrm{b},\) jsou stejně velké opačného směru a jejich výslednice je nulová. Zrychlení auta ve směru osy y je také nulové.
Vyjádření brzdné síly:
Brzdnou sílu Fb, která je přímo úměrná okamžité rychlosti auta, můžeme vyjádřit vztahem:
\[F_\mathrm{b}\,=\,kv\,.\tag{4}\]Dosazením do vztahu (2) dostaneme:
\[ma\,=\,-kv\,.\tag{5}\]Zrychlení vyjádříme jako časovou změnu rychlosti:
\[m\frac{\mathrm{d}v}{\mathrm{d}t}\,=\,-kv\,.\tag{6}\]Průběh v(t):
Získali jsme diferenciální rovnici 1. řádu s konstantními koeficienty. Vyřešíme ji separací proměnných.
Rovnici (6) upravíme na tvar:
\[\frac{\mathrm{d}v}{v}\,=\,-\frac{k}{m}\mathrm{d}t\,.\]Obě strany integrujeme:
\[\ln|v|\,=\,-\frac{k}{m}t+C\,,\]kde C je konstanta.
Odlogaritmujeme:
\[|v|\,=\,e^{-\frac{k}{m}t+C}\,=\,e^{-\frac{k}{m}t}\cdot e^{C}\,.\]Rychlost nabývá kladných hodnot, proto nemusíme psát absolutní hodnotu. Konstantu eC označíme jako K:
\[v\,=\,K e^{-\frac{k}{m}t }.\]Konstantu K zjistíme z počátečních podmínek. V čase t = 0 s byla rychlost rovna v0. Platí tedy:
\[v_0\,=\,K e^{-\frac{k}{m}\cdot 0}.\]Odtud:
\[v_0\,=\,K\,.\]Pro závislost rychlosti na čase dostáváme:
\[v(t)\,=\,v_0\cdot e^{-\frac{k}{m}t}\ \,.\tag{7}\]Známe závislost rychlosti na čase.
Integrací získáme závislost dráhy na čase:
\[x(t)\,=\,\int{v(t)}\,\mathrm{d}t,\] \[x(t)\,=\,\int{v_0e^{-\frac{k}{m} t}}\,\mathrm{d}t,\] \[x(t)\,=\,-\frac{mv_0}{k}e^{-\frac{k}{m} t}+C.\]Konstantu C určíme z počátečních podmínek. V čase t0 = 0 s byla uražená dráha 0 m.
Platí tedy:
\[0\,=\,-\frac{mv_0}{k}e^{-\frac{k}{m}\cdot 0}+C,\] \[C\,=\,\frac{mv_0}{k}.\]Závislost dráhy na čase:
\[x(t)\,=\,-\,\frac{mv_0}{k}e^{-\frac{k}{m}\,\cdot t}\,+\,\frac{mv_0}{k},\] \[x(t)\,=\,\frac{mv_0}{k}\left(1\,-\,e^{-\frac{k}{m}t}\right).\tag{8}\]Čas, za který klesne počáteční rychlost auta na poloviční hodnotu:
Do vztahu (7) pro závislost rychlosti na čase dosadíme za \(v(t)\,=\,\frac{v_0}{2}\):
\[\frac{v_0}{2}\,=\,v_0e^{-\,\frac{k}{m}t},\] \[\frac{1}{2}\,=\,e^{-\frac{k}{m}t}.\]Rovnici zlogaritmujeme:
\[\ln\frac{1}{2}\,=\,-\,\frac{k}{m}t,\] \[-\,\frac{m}{k}\,\ln\frac{1}{2}\,=\,t,\] \[\frac{m}{k}\,\ln2\,=\,t.\tag{9}\]Do vztahu (9) dosadíme číselně:
\[t\,=\,\frac{1\,000}{231}\,\cdot 0{,}693\,=\,\frac{693}{231}\,=\,3\,\textrm{s}\,.\]CELKOVÁ ODPOVĚĎ
Pro závislost rychlosti na čase platí \(v(t)\,=\,v_0 e^{-\frac{k}{m}t}\).
Pro závislost dráhy na čase platí \(x(t)\,=\,\frac{mv_0}{k}\left(1\,-\,e^{-\frac{k}{m}t}\right)\).
Rychlost auta klesne na poloviční hodnotu počáteční rychlosti za 3 s.



