Koule - dokonale nepružná srážka
Úloha číslo: 154
Dvě koule o hmotnosti m1 a m2 se pohybují proti sobě po stejné přímce a srazí se. Srážka je dokonale nepružná, tj. koule po srážce od sebe neodskočí a pohybují se dále společně. Kinetická energie E1 první koule je před srážkou dvacetkrát větší než kinetická energie E2 druhé koule. Je možné, aby se koule po srážce pohybovaly ve směru pohybu koule s menší kinetickou energií? Jaká podmínka pro to musí být splněna?
Nápověda 1 - zákon zachování hybnosti
Při dokonale nepružné srážce platí zákon zachování hybnosti. Nakreslete si obrázek a napište tento zákon pro naši situaci.
Nápověda 2 - energie koulí
Jaká je kinetická energie koulí před srážkou? Vyjádřete si z energií jednotlivých koulí rychlosti.
Odpověď
Společný pohyb nastane ve směru koule s menší energií, pokud bude hmotnost této koule alespoň dvacetkrát větší než hmotnost koule s větší energií.
Celkové řešení
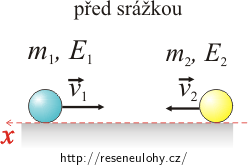

m1…hmotnost první koule
m2…hmotnost druhé koule
v1…počáteční rychlost první koule
v2…počáteční rychlost druhé koule
v…výsledná rychlost obou koulí
E1…kinetická energie první koule
E2…kinetická energie druhé koule
Zákon zachování hybnosti (ZZH):
Součet hybností těles v izolované soustavě je konstantní nebo-li celková hybnost izolované soustavy se zachovává.
\[\mathrm{ZZH:} \qquad \vec{p_1}+\vec {p_2}\,=\,\vec{p}\]\(\vec{p}\)…celková hybnost soustavy
\(\vec{p_1}\)…hybnost koule o hmotnosti m1
\(\vec{p_2}\)…hybnost koule o hmotnosti m2
\[m_1\vec{v_1}+m_2\vec{v_2}\,=\,\left(m_1+m_2\right)\vec{v}\]Protože se koule pohybují po přímce, můžeme rovnici napsat skalárně. Osu x orientujeme ve směru pohybu koule m2:
\[-m_1v_1+m_2v_2\,=\,\left(m_1+m_2\right)v.\]Aby se systém pohyboval ve směru koule s menší energií E2, musí platit:
\[m_2v_2\,>\,m_1v_1.\tag{1}\]Kinetická energie koule o hmotnosti m1 je:
\[E_1\,=\,\frac {1}{2}m_1v_1^2.\]Kinetická energie koule o hmotnosti m2 je:
\[E_2\,=\,\frac {1}{2}m_2v_2^2.\]Odtud vyjádříme rychlosti v1, v2:
\[v_1\,=\,\sqrt {\frac{2E_1}{m_1}},\] \[v_2\,=\,\sqrt {\frac{2E_2}{m_2}}.\]Dosadíme do vztahu (1):
\[m_2\sqrt{\frac{2E_2}{m_2}}\,>\,m_1\sqrt{\frac{2E_1}{m_1}}.\]Odtud dostaneme:
\[\frac{m_2}{m_1}\,>\,\frac{E_1}{E_2}.\]Víme, že energie E1 je dvacetkrát větší než energie E2, proto:
\[\frac{m_2}{m_1}\,>\,20,\] \[m_2\,>\,20m_1.\]Odpověď: Společný pohyb nastane ve směru koule s menší energií, pokud bude hmotnost této koule alespoň dvacetkrát větší než hmotnost koule s větší energií.





