Cisterna ve tvaru komolého kužele
Úloha číslo: 1002
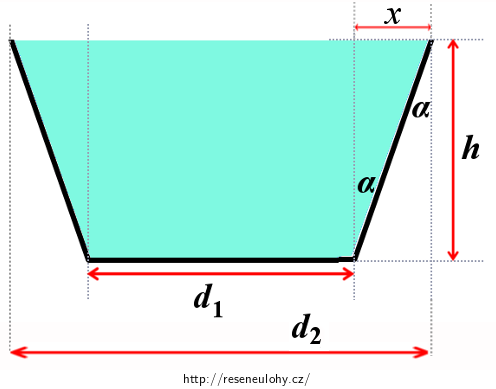
Otevřená cisterna, která má tvar komolého rotačního kužele s průměrem dolní podstavy 1,2 m a úhlem mezi boční stěnou a svislicí 30°, je naplněna vodou do výšky 3 m. Nad hladinou vody je tlak vzduchu 0,1 MPa. Určete:
- Objem a hmotnost vody v cisterně.
- Tlak vody u dna cisterny.
- Velikost síly, kterou působí voda na dno.
- Velikost výsledné síly, kterou působí voda na kuželovou stěnu.
Zápis
d1 = 1,2 m průměr dolní podstavy komolého kužele α = 30° úhel mezi boční stěnou a svislicí h = 3 m výška vody v cisterně p1 = 0,1 MPa tlak vzduchu nad hladinou vody V = ? objem vody v cisterně m = ? hmotnost vody v cisterně p = ? tlak vody u dna cisterny F = ? velikost síly, kterou působí voda na dno cisterny Fs = ? výsledna síla na kuželovou stěnu Nápověda 1 (k části a.)
Voda v cisterně má tvar komolého rotačního kužele. Jak se spočítá objem tohoto tělesa?
Nápověda 2 (k části a.)
Které veličiny ve vzorci pro objem komolého rotačního kužele neznáte? Nakreslete si obrázek a vyjádřete je pomocí zadaných veličin (zadaný úhel by vás měl vést k použití nějaké goniometrické funkce). Dosaďte do vztahu pro objem.
Nápověda 3 (k části a.)
Hmotnost vody dopočítejte pomocí její hustoty.
Nápověda 4 (k části b.)
Jaké „druhy“ tlaku přispívají k celkovému tlaku vody u dna cisterny? Určete je a dosazením zadaných veličin určete výsledný tlak.
Nápověda 5 (k části c.)
K výpočtu velikosti síly, kterou působí voda na dno cisterny, použijte definiční vztah pro tlak.
Nápověda 6 (k části d.)
Uvažte, jaké síly na kapalinu v nádobě působí. Jaká musí být jejich výslednice? Vyjádřete odtud velikost síly, kterou působí nádoba na vodu uvnitř.
Nápověda 7 (k části d.)
Chceme určit sílu, kterou působí voda na kuželovou stěnu. Už víte, že podle zákona akce a reakce můžeme namísto ní určit sílu, kterou působí naopak kuželová stěna na vodu – dostaneme také správný výsledek, tyto síly jsou co do velikosti stejné.
Budeme tedy určovat velikost výsledné síly Fs, kterou působí stěna nádoby na vodu. V části c jsme již určili velikost síly F, kterou působí dno na vodu (resp. voda na dno). Jak síly Fs a F souvisí se silou Fn?
Nápověda 8 (k části d.)
Spojením úvah a vztahů (7) a (8) vyjádřete sílu Fs, kterou působí kuželová stěna nádoby na vodu (tj. také voda na kuželovou stěnu). Za jednotlivé síly dosaďte ze známých vztahů a číselně dopočítejte sílu Fs.
Celkové řešení
Část a:
Pro objem komolého kužele platí:
\[V\,=\,\frac{1}{3}{\pi}h(r_1^2\,+\,r_1r_2\,+\,r_2^2)\,,\tag{1}\]kde r1 a r2 jsou poloměry podstav a h výška komolého kužele.
Poloměr r1 snadno dostaneme ze znalosti průměru podstavy d1:
\[r_1\,=\,\frac{d_1}{2}\,.\tag{2}\]Poloměr r2 vyčteme z obrázku:
\[d_2\,=\,d_1\,+\,2x\,.\]Platí:
\[\tan{\alpha}\,=\,\frac{x}{h}\,.\]Odtud:
\[x\,=\,h\tan{\alpha}\,.\]Pak:
\[d_2\,=\,d_1\,+\,2h\tan{\alpha}\,,\] \[r_2\,=\,\frac{d_2}{2}\,=\,\frac{d_1}{2}\,+\,h\tan{\alpha}\,.\tag{3}\]Dosazením (2) a (3) do (1) dostáváme:
\[V\,=\,\frac{1}{3}{\pi}h(\frac{d_1^2}{4}\,+\,\frac{d_1}{2}(\frac{d_1}{2}\,+\,h\tan{\alpha})\,+\,(\frac{d_1}{2}\,+\,h\tan{\alpha})^2)\,\\=\,\frac{1}{12}{\pi}h(3d_1^2\,+\,6hd_1\tan{\alpha}\,+\,4h^2\tan^2{\alpha})\,.\]Číselně:
\[V\,=\,\frac{3{\pi}}{12}{\cdot}(3{\cdot}1{,}2^2\,+\,6{\cdot}3{\cdot}1{,}2{\cdot}\tan{30}\,+\,4{\cdot}3^2{\cdot}\tan^2{30})\,\mathrm{m}^3\,\\\dot=22{,}6\,\mathrm{m}^3\,.\]Hmotnost vody určíme pomocí její hustoty, která je definována jako podíl hmotnosti a objemu dané látky. Z definice vyjádříme hmotnost, dosadíme objem dopočítaný v předcházející části příkladu a číselně dopočítáme:
\[\rho\,=\,\frac{m}{V}\,\Rightarrow\,m\,=\,{\rho}V\,=\,1000{\cdot}22{,}6\,\mathrm{kg}\,=\,22{,}6\,\mathrm{t}\,.\]
Část b:
Tlak vody u dna cisterny je součtem:
- atmosférického tlaku vzduchu p1 nad vodní hladinou,
- hydrostatického tlaku ph způsobeného tíhou vodního sloupce v cisterně.
Tedy:
\[p\,=\,p_1\,+\,p_\mathrm{h}\,.\tag{4}\]Přitom pro velikost hydrostatického tlaku platí:
\[p_\mathrm{h}\,=\,h{\rho}g\,,\tag{5}\]kde h je výška vodního sloupce, ρ hustota kapaliny a g tíhové zrychlení.
Dosazením vztahu (5) do vztahu (4) dostáváme:
\[p\,=\,p_1\,+\,h{\rho}g\,.\]Číselně:
\[p\,=(\,1{\cdot}10^5\,+\,3{\cdot}1000{\cdot}9{,}81)\,\mathrm{Pa}\,\dot=\,1{,}3{\cdot}10^5\,\mathrm{Pa}\,.\]
Část c:
Tlak je definován jako podíl síly působící na danou plochu a obsahu této plochy. V našem případě platí:
\[p\,=\,\frac{F}{S}\,,\]kde p je celkový tlak vody u dna cisterny, S obsah její dolní podstavy a F neznámá síla. Snadnou úpravou dostáváme:
\[F\,=\,pS\,.\tag{6}\]Protože dolní podstava má tvar kruhu o poloměru d1/2, můžeme vztah (6) upravit takto:
\[F\,=\,p{\cdot}{\pi}\frac{d_1^2}{4}\,.\] Číselně: \[F\,\dot=\,1{,}3{\cdot}10^5{\cdot}{\pi}{\cdot}\frac{1{,}2^2}{4}\,\mathrm{N}\,\dot=\,1{,}47{\cdot}10^5\,\mathrm{N}\,.\]
Část d:
Vyjdeme z toho, že na celý objem vody působí tyto síly:
- tlaková síla F1 směrem svisle dolů (tato síla je způsobená vnějším tlakem vzduchu p1),
- tíhová síla FG směrem svisle dolů,
- tlaková síla Fn, kterou působí nádoba.
Voda je jako celek v klidu (neuvažujeme vnitřní strukturu kapaliny a zanedbáváme tak například difuzi jejích částic), výslednice těchto sil musí být nulová. Síla Fn tedy musí působit svisle vzhůru a její velikost musí být rovna součtu tlakové síly F1 a tíhové síly:
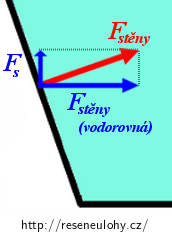
\[F_\mathrm{n}\,=\,F_\mathrm{G}\,+\,F_1\,.\tag{7}\]Nádoba působí na vodu svými stěnami a svým dnem. Dno tlačí kolmo vzhůru silou velikosti F. Stěna tlačí na vodu v každém bodě kolmo k povrchu. Vodorovné složky sil se vyruší, svislé se posčítají ve výslednici Fs:
Celkové působení nádoby lze tedy vyjádřit jako součet sil F a Fs:
\[F_\mathrm{n}\,=\,F\,+\,F_\mathrm{s} \,.\tag{8}\]V tomto vztahu F značí velikost síly, kterou působí voda na dno nádoby (a tedy i dno nádoby na vodu) – tuto sílu jsme již vypočítali v části c; Fs pak značí velikost hledané výsledné síly, kterou voda působí na stěnu nádoby.
Spojením vztahů (7) a (8) – nebo přirozenou úvahou – dostáváme:
\[F\,+\,F_\mathrm{s}\,=\,F_\mathrm{G}\,+\,F_1\,\Rightarrow\,F_\mathrm{s}\,=\,F_\mathrm{G}\,+\,F_1\,-\,F\,.\]Za tíhovou sílu FG a tlakovou sílu F1 dosadíme:
\[F_\mathrm{s}\,=\,mg\,+\,p_1S_2\,-\,F\,,\tag{9}\]kde m je hmotnost vody v cisterně, g tíhové zrychlení, p1 tlak vzduchu nad hladinou vody a S2 obsah plochy vymezené vodní hladinou (tj. horní podstavy komolého kužele). Tento obsah určíme jako obsah kruhu o poloměru r2, který je vyjádřen vztahem (3). Pak lze vztah (9) upravit následovně:
\[F_\mathrm{s}\,=\,mg\,+\,p_1{\pi}{(\frac{d_1}{2}\,+\,h\tan{\alpha})}^2\,-\,F\,.\]Číselně:
\[F_\mathrm{s}\,\dot=\,(22600{\cdot}9{,}81\,+\,1{\cdot}10^5{\pi}{(\frac{1{,}2}{2}\,+\,3\tan{30^{\circ}})}^2\,-\,1{,}47{\cdot}10^5)\,\mathrm{N}\\\dot=\,1780\,\mathrm{kN}\,.\]Odpověď
- Objem vody v cisterně je 22,6 m3, hmotnost této vody je 22,6 t.
- Tlak vody u dna cisterny je přibližně 130 kPa.
- Tlaková síla působící na dno cisterny má velikost přibližně 147 kN.
- Výsledná tlaková síla působící na kuželovou stěnu nádoby má velikost přibližně 1780 kN.