Housenka
Úloha číslo: 762
Na obrázku je zaznamenaná stopa housenky s časovými údaji, kdy kde byla.
Obrázek:
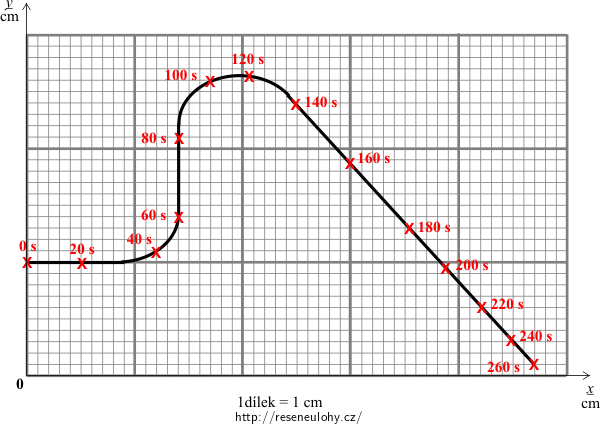
a) Sestavte podle obrázku tabulku závislosti ulezené dráhy na čase a nakreslete graf.
b) Odpovězte na následující otázky:
1. Jakou vzdálenost housenka přibližně ulezla? (Zakřivené úseky dráhy můžete odměřit například pomocí niti.)
2. Jakou vzdálenost ulezla mezi 20. s a 40. s a mezi 100. s a 120. s?
3. Mezi kterými dvěma měřeními byla ulezená vzdálenost největší a mezi kterými nejmenší?
4. Poznáte z grafu, zda housenka někdy stála? Podle čeho?
c) Určete souřadnice housenky v čase 0 s, 20 s, 80 s, 120 s, 140 s, 260 s.
d) Určete průměrnou rychlost housenky během doby, co jste ji sledovali.
e) Určete průměrné rychlosti housenky v jednotlivých dvacetisekundových intervalech a zapište je do tabulky. Údaje vyneste do grafu.
f) Kdy lezla housenka nejrychleji a kdy nejpomaleji? Jak to poznáte z grafu rychlosti a jak z grafu dráhy?
Nápověda 1 pro a):
Uvědomte si, co obrázek představuje a kde je v něm schovaná dráha.
Tabulku závislosti ulezené dráhy housenky na čase i graf pak snadno sestavíte.
Nápověda 2 pro b)1:
Vzdálenost, kterou housenka ulezla, můžete na obrázku odměřit například pomocí niti nebo ji můžete zjistit rovnou z grafu (resp. z tabulky) z bodu a).
Nápověda 3 pro b)2:
V tabulce z bodu a) máte zaznamenanou ulezenou dráhu housenky v jednotlivých časech.
Snadno v ní najdete vzdálenost, kterou housenka ulezla mezi 20. s a 40. s nebo mezi 100. s a 120. s.
Nápověda 4 pro b)3:
Hledané úseky najdete snadno pohledem na stopu housenky.
Najít je můžete i v tabulce z bodu a), kde máte zaznamenanou ulezenou dráhu housenky v jednotlivých časech. Je třeba zjistit, mezi kterými dvěma měřeními byla ulezená vzdálenost housenky největší a mezi kterými nejmenší.
Nápověda 5 pro b)4:
Jak by vypadala křivka v grafu závislosti ulezené dráhy housenky na čase (z bodu a)), kdyby housenka v libovolném dvacetisekundovém intervalu stála? Jaká by byla její ulezená vzdálenost?
Promyslete si, jestli by se z grafu dalo poznat, kdyby housenka stála třeba jen 10 s.
Nápověda 6 pro c):
Souřadnice housenky v jednotlivých časových okamžicích určíte z obrázku ze zadání. Na vodorovné ose odečtete x-ovou souřadnici, na svislé ose pak y-ovou souřadnici housenky.
Nápověda 7 pro d):
Z tabulky závislosti ulezené dráhy housenky na čase (z bodu a)) zjistěte celkovou dobu, po kterou jsme pohyb housenky sledovali, a celkovou dráhu, kterou za celkovou dobu ulezla.
Jak z těchto údajů určíte průměrnou rychlost housenky?
Nápověda 8 pro e):
Z tabulky závislosti ulezené dráhy housenky na čase (z bodu a)) zjistěte přírůstky dráhy housenky v jednotlivých dvacetisekundových intervalech.
Znáte-li dráhu ulezenou v daném časovém intervalu a jeho délku, spočítáte příslušnou průměrnou rychlost podobně jako v předchozím bodě.
Nápověda 9 pro f):
Ke zjištění, kdy lezla housenka nejrychleji nebo nejpomaleji, vám pomůže odpověď na otázku b) 3 či tabulka z předchozí nápovědy nebo pohled do grafů.
Uvědomte si, že lezla-li housenka v daném dvacetisekundovém intervalu nejrychleji (resp. nejpomaleji), byla v tomto intervalu její průměrná rychlost největší (resp. nejmenší). Rozmyslete si, jak to ovlivní tvar křivky grafu závislosti ulezené dráhy housenky na čase.
CELKOVÉ ŘEŠENÍ:
a):
V obrázku je zachycená křivka, po které housenka lezla (trajektorie). Abychom zjistili ulezenou dráhu v daném čase, musíme změřit nebo pomocí čtvercové sítě v obrázku odhadnout délku této křivky od nuly do daného času.
Tabulka závislosti ulezené dráhy housenky na čase:
čas/s 0 20 40 60 80 100 120 140 160 180 200 220 240 260 dráha/cm 0 5 12 16 23 29 33 38 45 53 58 63 67 70 Graf závislosti ulezené dráhy housenky na čase:
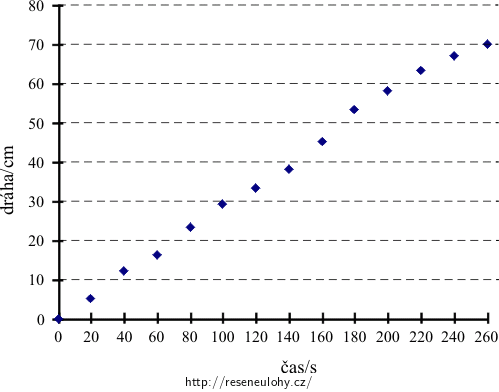
b) 1:
Z grafu závislosti ulezené dráhy na čase (z bodu a)) nebo rovnou z tabulky závislosti ulezené dráhy na čase (z bodu a)) vidíme, že housenka ulezla vzdálenost přibližně 70 cm.
b) 2:
Z tabulky z bodu a) závislosti ulezené dráhy housenky na čase odečteme:
Ve dvacáté sekundě měla housenka ulezeno 5 cm, v čtyřicáté sekundě měla housenka ulezeno 12 cm, mezi dvacátou a čtyřicátou sekundou tedy ulezla 7 cm.
Obdobně ve sté sekundě měla housenka ulezeno 29 cm a ve stodvacáté 33 cm, mezi stou a stodvacátou sekundou housenka tedy ulezla 4 cm.
b) 3:
Z tabulky z bodu a) závislosti ulezené dráhy housenky na čase lze vyčíst:
Největší vzdálenost, kterou housenka ulezla mezi dvěma měřeními, byla vzdálenost mezi stošedesátou a stoosmdesátou sekundou, a to 8 cm.
Nejmenší vzdálenost, kterou housenka ulezla mezi dvěma měřeními, byla vzdálenost mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou, a to 3 cm.
b) 4:
Pokud by housenka stála celých dvacet sekund, byla by křivka v grafu závislosti ulezené dráhy housenky na čase (z bodu a)) v daném úseku vodorovná. Ulezená vzdálenost housenky v daném dvacetisekundovém úseku by byla nulová.
Housenka ale mohla stát třeba jen deset sekund a pak kus ulézt a to z grafu nepoznáme.
c):
Souřadnice housenky v jednotlivých časových okamžicích určíme z obrázku ze zadání. Na vodorovné ose odečteme x-ovou souřadnici, na svislé ose pak y-ovou souřadnici housenky.
Platí:
V čase 0 s měla housenka souřadnice:
\[x=0\,\mathrm{cm},\] \[y=10\,\mathrm{cm}.\]V čase 20 s měla housenka souřadnice:
\[x=5\,\mathrm{cm},\] \[y=10\,\mathrm{cm}.\]V čase 80 s měla housenka souřadnice:
\[x=14\,\mathrm{cm},\] \[y=21\,\mathrm{cm}.\]V čase 140 s měla housenka souřadnice:
\[x=25\,\mathrm{cm},\] \[y=24\,\mathrm{cm}.\]V čase 260 s měla housenka souřadnice:
\[x=47\,\mathrm{cm},\] \[y=1\,\mathrm{cm}.\]d):
Z tabulky závislosti ulezené dráhy housenky na čase (z bodu a)) zjistíme celkovou dobu, po kterou jsme pohyb housenky sledovali, a označíme si ji tc. Dále z tabulky zjistíme celkovou dráhu, kterou housenka za celkovou dobu ulezla, a označíme ji sc.
Platí:
\[t_\mathrm{c}=260\,\mathrm{s},\] \[s_\mathrm{c}=70\,\mathrm{cm}.\]Z těchto údajů určíme průměrnou rychlost housenky během doby, co jsme ji sledovali:
\[v_\mathrm{p}=\frac{s_\mathrm{c}}{t_\mathrm{c}},\] \[v_\mathrm{p}=\frac{70\,\mathrm{cm}}{260\,\mathrm{s}}=0{,}27\,\mathrm{cm\cdot s^{-1}}=2{,}7\,\mathrm{mm\cdot s^{-1}}.\]e):
Z tabulky závislosti ulezené dráhy housenky na čase (bod a)) zjistíme, jakou dráhu ulezla housenka v jednotlivých dvacetisekundových intervalech.Průměrnou rychlost v daném intervalu (v mm/s) spočítáme tak, že vydělíme dráhu ulezenou v příslušném intervalu (v mm) časem 20 s.
Tabulka ulezené dráhy v závislosti na čase, přírůstků dráhy a průměrných rychlostí v jednotlivých časových intervalech:
čas/s 0 20 40 60 80 100 120 140 160 180 200 220 240 260 dráha/cm 0 5 12 16 23 29 33 38 45 53 58 63 67 70 přírůstek dráhy/cm 5 7 4 7 6 4 5 7 8 5 5 4 3 průměrná rychlost/(mm/s) 2,5 3,5 2,0 3,5 3,0 2,0 2,5 3,5 4,0 2,5 2,5 2,0 1,5 Graf průměrných rychlostí housenky v jednotlivých dvacetisekundových intervalech:
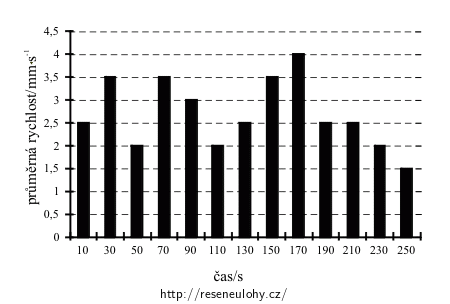
f):
Ke zjištění, kdy lezla housenka nejrychleji nebo nejpomaleji, pomůže odpověď na otázku b) 3, tabulka z předchozí nápovědy nebo pohled do grafů.
Určení z tabulky:
Z tabulky z bodu e) (řešení předchozí nápovědy 8) lze vyčíst:
Největší vzdálenost, kterou housenka ulezla mezi dvěma měřeními, byla vzdálenost mezi stošedesátou a stoosmdesátou sekundou, a to 8 cm. Protože měření provádíme ve stále stejném dvacetisekundovém intervalu, znamená to, že v této době byla její průměrná rychlost nejvyšší.
Housenka tedy lezla nejrychleji mezi stošedesátou a stoosmdesátou sekundou.
Nejmenší vzdálenost, kterou housenka ulezla mezi dvěma měřeními, byla vzdálenost mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou, a to 3 cm. Protože měření provádíme ve stále stejném dvacetisekundovém intervalu, znamená to, že v této době byla její průměrná rychlost nejnižší.
Housenka tedy lezla nejpomaleji mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou.
Určení z grafu:
Jak již bylo řečeno, lezla-li housenka v daném dvacetisekundovém intervalu nejrychleji (resp.nejpomaleji), byla v tomto intervalu její průměrná rychlost největší (resp.nejmenší).
Z grafu průměrné rychlosti housenky v jednotlivých dvacetisekundových intervalech tedy vyplývá:
Housenka lezla nejrychleji mezi stošedesátou a stoosmdesátou sekundou, protože sloupec v grafu průměrných rychlostí je nejvyšší.
Housenka lezla nejpomaleji mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou, protože sloupec v grafu průměrných rychlostí je nejnižší.
Z grafu závislosti ulezené dráhy housenky na čase vyplývá:
Housenka lezla nejrychleji mezi stošedesátou a stoosmdesátou sekundou, protože křivka v grafu dráhy je nejstrmější.
Housenka lezla nejpomaleji mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou, protože křivka v grafu dráhy je nejméně strmá.
Odpověď:
a):
Tabulka závislosti ulezené dráhy housenky na čase:
čas/s 0 20 40 60 80 100 120 140 160 180 200 220 240 260 dráha/cm 0 5 12 16 23 29 33 38 45 53 58 63 67 70 Graf závislosti ulezené dráhy housenky na čase:
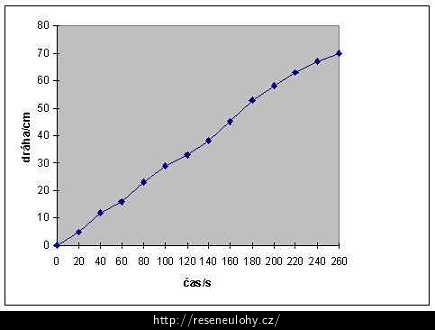
b) 1:
Housenka ulezla vzdálenost přibližně 70 cm.
b) 2:
Mezi dvacátou a čtyřicátou sekundou housenka ulezla 7 cm.
Mezi stou a stodvacátou sekundou housenka ulezla 4 cm.
b) 3:
Největší vzdálenost, kterou housenka ulezla mezi dvěma měřeními, byla vzdálenost mezi stošedesátou a stoosmdesátou sekundou, a to 8 cm.
Nejmenší vzdálenost, kterou housenka ulezla mezi dvěma měřeními, byla vzdálenost mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou, a to 3 cm.
b) 4:
Pokud by housenka stála celých dvacet sekund, byla by křivka v grafu závislosti ulezené dráhy housenky na čase (z bodu a)) v daném úseku vodorovná. Ulezená vzdálenost housenky v daném dvacetisekundovém úseku by byla nulová.
Housenka ale mohla stát třeba jen deset sekund a pak kus ulézt a to z grafu nepoznáme.
c):
V čase 0 s měla housenka souřadnice:
\[x=0\,\mathrm{cm},\] \[y=10\,\mathrm{cm}.\]V čase 20 s měla housenka souřadnice:
\[x=5\,\mathrm{cm},\] \[y=10\,\mathrm{cm}.\]V čase 80 s měla housenka souřadnice:
\[x=14\,\mathrm{cm},\] \[y=21\,\mathrm{cm}.\]V čase 140 s měla housenka souřadnice:
\[x=25\,\mathrm{cm},\] \[y=24\,\mathrm{cm}.\]V čase 260 s měla housenka souřadnice:
\[x=47\,\mathrm{cm},\] \[y=1\,\mathrm{cm}.\]d):
Průměrná rychlost housenky během doby, co jsme ji sledovali, byla:
\[v_\mathrm{p} = \frac{s_\mathrm{c}}{t_\mathrm{c}} = \frac{70\,\mathrm{cm}}{260\,\mathrm{s}}= 2{,}7\,\mathrm{mm\cdot s^{-1}}.\]e):
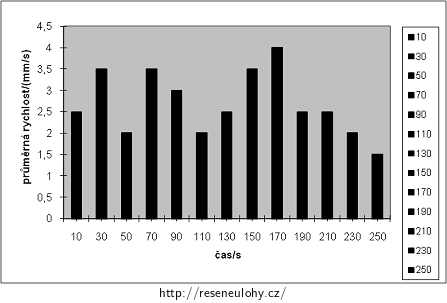
Tabulka ulezené dráhy v závislosti na čase, přírůstků dráhy a průměrných rychlostí v jednotlivých časových intervalech:
čas/s 0 20 40 60 80 100 120 140 160 180 200 220 240 260 dráha/cm 0 5 12 16 23 29 33 38 45 53 58 63 67 70 přírůstek dráhy/cm 5 7 4 7 6 4 5 7 8 5 5 4 3 průměrná rychlost/(mm/s) 2,5 3,5 2,0 3,5 3,0 2,0 2,5 3,5 4,0 2,5 2,5 2,0 1,5 Graf průměrných rychlostí housenky v jednotlivých dvacetisekundových intervalech:
f):
Určení z tabulky:
Housenka lezla nejrychleji mezi stošedesátou a stoosmdesátou sekundou.
Housenka lezla nejpomaleji mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou.
Určení z grafu:
Housenka lezla nejrychleji mezi stošedesátou a stoosmdesátou sekundou, protože schod v grafu průměrných rychlostí je nejvyšší a křivka v grafu dráhy je nejstrmější.
Housenka lezla nejpomaleji mezi dvěstěčtyřicátou a dvěstěšedesátou sekundou, protože schod v grafu průměrných rychlostí je nejnižší a křivka v grafu dráhy je nejméně strmá.




