Počítání s barometrem

Úloha číslo: 998

Princip funkce barometru je tento: úzká skleněná, na jednom konci zatavená trubice délky 1 metr je částečně naplněna rtutí a ponořena svisle do misky rovněž naplněné rtutí.

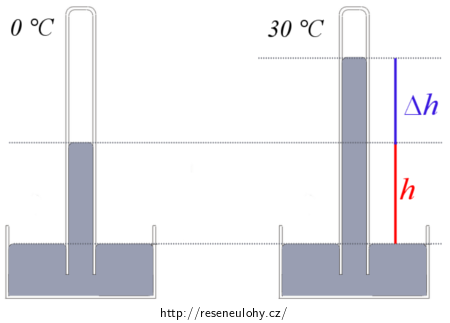
Ráno, při teplotě 0 °C, sahá sloupec rtuti v barometru do výšky h. V předpovědi počasí bylo právě uvedeno, že atmosférický tlak je 99,7 kPa a tlaková tendence je setrvalá (tj. atmosférický tlak se během experimentu nemění).

Později sluníčko ohřeje povrch Země, od něhož se následně ohřeje i vzduch (a tedy i rtuť) na 30 °C. Jak se změní výška rtuťového sloupce v barometru?

Hustota rtuti při 0 °C je 13 595 kg·m⁻³ a při 30 °C je 13 521 kg·m⁻³.

Zápis

p_a = 99,7 kPa = 99,7·10³ Pa	atmosférický tlak
ρ₀ = 13 595 kg·m⁻³	hustota rtuti při 0 °C
ρ₃₀ = 13 521 kg·m⁻³	hustota rtuti při 30 °C
h₀ = 1 m	délka trubice
Δh = ?	změna výšky rtuťového sloupce

Nápověda 1
Princip fungování rtuťového barometru úzce souvisí s tzv. Toricelliho experimentem. O jaký experiment šlo?
Řešení nápovědy 1
Italský fyzik a matematik Evangelista Toricelli provedl experiment, při kterém naplnil přibližně metr dlouhou na jednom konci zatavenou skleněnou trubici rtutí a zataveným koncem vzhůru ji umístil do nádobky se rtutí (viz obrázek v zadání). Hladina rtuti v trubici poklesla a ustálila se na určité výšce.
Nápověda 2
Proč se ve výše uvedeném experimentu výška hladiny rtuti v trubici ustálí? (Tj. ani nezůstane na původní úrovni, ani neklesne až na úroveň volné hladiny v nádobě?) Jak lze tento fakt využít k měření atmosférického tlaku?
Řešení nápovědy 2
Na volnou hladinu rtuti v nádobce působí tlaková síla vzduchu, která nutí rtuť stoupat trubicí vzhůru. Naopak směrem svisle dolů působí na kapalinu (rtuť) v trubici její vlastní tíha. (Tlak rtuťových par nad hladinou v trubici neuvažujeme.)

Při určité výšce rtuťového sloupce dochází k vyrovnání hydrostatického tlaku tohoto sloupce p_h a tlaku vzduchu p_a (tj. tlaku atmosférického):
\[p_\mathrm{a}\,=\,p_\mathrm{h}\,.\tag{1}\]
Rtuť v takovém případě nemá důvod stoupat ani klesat. Měření atmosférického tlaku lze tedy takto převést na měření tlaku hydrostatického.
Nápověda 3
Pomocí předcházející úvahy vyjádřete atmosférický tlak jako hydrostatický tlak rtuťového sloupce:
- při teplotě 0 °C ( p_h1),
- při teplotě 30 °C ( p_h2).
Řešení nápovědy 3
Podle (1) lze atmosférický tlak při teplotě 0 °C vyjádřit jako hydrostatický tlak rtuťového sloupce. Ten má v danou chvíli výšku h, platí tedy:
\[p_\mathrm{a1}\,=\,p_\mathrm{h1}\,=\,h{\rho}_0g\,.\tag{2}\]
Atmosférický tlak při teplotě 30 °C lze opět vyjádřit jako hydrostatický tlak rtuťového sloupce. Platí:
\[p_\mathrm{a2}\,=\,p_\mathrm{h2}\,=\,h_2{\rho}_{30}g\,.\tag{3}\]
Nápověda 4
Jaký je vztah mezi atmosférickým tlakem při teplotě 0 °C a při teplotě 30 °C?

Jaká bude výška hladiny rtuti při 30 °C ve srovnání s výškou při 0 °C?
Řešení nápovědy 4
Dle zadání se atmosférický tlak během experimentu nemění, je tedy p_a1 = p_a2 = p_a.

Platí tedy:
\[h{\rho}_0g\,=\,h_2{\rho}_{30}g\,.\]
Protože je hustota rtuti při 30 °C nižší než při 0 °C, bude při 30 °C její hladina výše. Označíme-li rozdíl hladin Δh, platí:
\[p_\mathrm{a}\,=\,p_\mathrm{h2}\,=\,(h+{\Delta}h){\rho}_{30}g\,.\tag{4}\]
Nápověda 5
Ze vztahu (2) vyjádřete původní výšku sloupce h při 0 °C a dosaďte do vztahu (4). Odtud již přímo vyjádřete Δh.
Řešení nápovědy 5
Ze vztahu (2) plyne:
\[h\,=\,\frac{p_\mathrm{a}}{{\rho_0}g}\,.\tag{5}\]
Dosazením (5) do (4) dostáváme:
\[p_\mathrm{a}\,=\,(\frac{p_\mathrm{a}}{{\rho_0}g}\,+\,{\Delta}h)\rho_{30}g\,=\,\frac{{p_\mathrm{a}}{\rho_{30}}}{\rho_0}\,+\,{\Delta}h{\rho_{30}}g\,.\tag{6}\]
Přímo z (6) pak dostáváme:
\[{\Delta}h\,=\,\frac{p_\mathrm{a}}{\rho_{30}g}(1\,-\,\frac{\rho_{30}}{\rho_0})\,.\]
Číselně:
\[{\Delta}h\,=\,\frac{99700}{13521{\cdot}9{,}81}(1\,-\,\frac{13521}{13595})\,\mathrm{m}\,\dot=\,4{,}1\,\mathrm{mm}\,.\]
Celkové řešení
Princip měření tlaku rtuťovým barometrem úzce souvisí s tzv. Toricelliho experimentem. Italský fyzik a matematik Evangelista Toricelli provedl experiment, při kterém naplnil přibližně metr dlouhou na jednom konci zatavenou skleněnou trubici rtutí a zataveným koncem vzhůru ji umístil do nádobky se rtutí (viz obrázek v zadání). Hladina rtuti v trubici poklesla a ustálila se na určité výšce.

Tuto skutečnost vysvětlíme pomocí rovnosti tlaků. Na volnou hladinu rtuti v nádobce působí tlaková síla vzduchu, která nutí rtuť stoupat trubicí vzhůru. Naopak směrem svisle dolů působí na kapalinu (rtuť) v trubici její vlastní tíha. (Tlak rtuťových par nad hladinou v trubici neuvažujeme.)

Při určité výšce rtuťového sloupce dochází k vyrovnání hydrostatického tlaku tohoto sloupce p_h a tlaku vzduchu p_a (tj. tlaku atmosférického):
\[p_\mathrm{a}\,=\,p_\mathrm{h}\,.\tag{1}\]
Rtuť v takovém případě nemá důvod stoupat ani klesat. Měření atmosférického tlaku lze tedy takto převést na měření tlaku hydrostatického.

Podle (1) lze atmosférický tlak při teplotě 0 °C vyjádřit jako hydrostatický tlak rtuťového sloupce. Ten má v danou chvíli výšku h, platí tedy:
\[p_\mathrm{a1}\,=\,p_\mathrm{h1}\,=\,h{\rho}_0g\,.\tag{2}\]
Atmosférický tlak při teplotě 30 °C lze opět vyjádřit jako hydrostatický tlak rtuťového sloupce.

Platí:
\[p_\mathrm{a2}\,=\,p_\mathrm{h2}\,=\,h_2{\rho}_{30}g\,.\tag{3}\]
Podle zadání se atmosférický tlak během experimentu nemění, je tedy p_a1 = p_a2 = p_a.

Platí tedy:
\[h{\rho}_0g\,=\,h_2{\rho}_{30}g\,.\]
Protože je hustota rtuti při 30 °C nižší než při 0 °C, bude při 30 °C její hladina výše. Označíme-li rozdíl hladin Δh, platí:
\[p_\mathrm{a}\,=\,p_\mathrm{h2}\,=\,(h+{\Delta}h){\rho}_{30}g\,.\tag{4}\]
Nyní již vyjádříme rozdíl Δh.

Ze vztahu (2) plyne:
\[h\,=\,\frac{p_\mathrm{a}}{{\rho_0}g}\,.\tag{5}\]
Dosazením (5) do (4) dostáváme:
\[p_\mathrm{a}\,=\,(\frac{p_\mathrm{a}}{{\rho_0}g}\,+\,{\Delta}h)\rho_{30}g\,=\,\frac{{p_\mathrm{a}}{\rho_{30}}}{\rho_0}\,+\,{\Delta}h{\rho_{30}}g\,.\tag{6}\]
Přímo z (6) pak dostáváme:
\[{\Delta}h\,=\,\frac{p_\mathrm{a}}{\rho_{30}g}(1\,-\,\frac{\rho_{30}}{\rho_0})\,.\]
Číselně:
\[{\Delta}h\,=\,\frac{99700}{13521{\cdot}9{,}81}(1\,-\,\frac{13521}{13595})\,\mathrm{m}\,\dot=\,4{,}1\,\mathrm{mm}\,.\]
Odpověď
Výška hladiny rtuťového sloupce v trubici stoupne při zvýšení teploty z 0 °C na 30 °C přibližně o 4,1 mm (za předpokladu neměnného atmosférického tlaku).