Kapilára s rtutí
Úloha číslo: 1155
Kapilára délky 50 cm je uzavřená na obou koncích. Obsahuje vzduch, který je rtuťovým sloupcem délky 10 cm rozdělen na dva vzduchové sloupce. Pokud je kapilára ve vertikální poloze, pak jsou vzduchové sloupce dlouhé 15 cm a 25 cm. Umístíme-li kapiláru do horizontální polohy, bude délka obou vzduchových sloupců 20 cm.
Jaký je tlak vzduchu v kapiláře, když je v horizontální poloze?
Zápis
\(l_\mathrm{k}=50\,\mathrm{cm}=0{,}5\,\mathrm{m}\) délka kapiláry \(l_\mathrm{Hg}=10\,\mathrm{cm}=0{,}1\,\mathrm{m}\) délka rtuťového sloupce \(l_\mathrm{v1}=15\,\mathrm{cm}=0{,}15\,\mathrm{m}\) délka prvního vzduchového sloupce, když je kapilára ve vertikální poloze \(l_\mathrm{v2}=25\,\mathrm{cm}=0{,}25\,\mathrm{m}\) délka druhého vzduchového sloupce, když je kapilára ve vertikální poloze \(l_\mathrm{h}=20\,\mathrm{cm}=0{,}2\,\mathrm{m}\) délka prvního a druhého vzduchového sloupce, když je kapilára v horizontální poloze \( p_\mathrm{h}= ?\,\mathrm{Pa}\) tlak vzduchu v kapiláře, když je v horizontální poloze Rozbor
Při řešení úlohy budeme považovat vzduch za ideální plyn a předpokládat, že se jeho teplota během obracení kapiláry nemění. Využijeme tedy Boyleův-Mariottův zákon pro vzduchové sloupce. Dále napíšeme vztahy pro tlakovou rovnováhu.
Nápověda 1
Nakreslete si obrázek kapiláry ve vertikální a horizontální poloze. Obrázek popište.
Nápověda 2
Napište, jaký je vztah mezi tlaky \(p_\mathrm{v1}\) a \(p_\mathrm{v2}\).
Nápověda 3
Co říká Boyleův-Mariottův zákon? Zformulujte ho pro vzduchové sloupce A a B.
Nápověda 4
Nápověda 5
Vyřešte číselně dosazením hodnot do (13).
Celkové řešení
Nakreslíme si obrázek kapiláry ve vertikální a horizontální poloze.
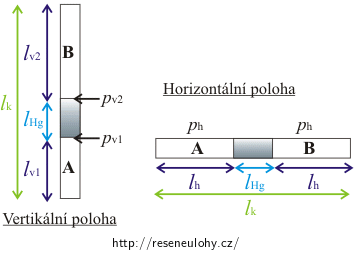
\(p_\mathrm{v1}\) je tlak spodní části rtuťového sloupce na vzduchový, když je kapilára ve vertikální poloze
\(p_\mathrm{v2}\) je tlak horní části rtuťového sloupce na vzduchový, když je kapilára ve vertikální poloze
\(A\) označuje první vzduchový sloupec
\(B\) označuje druhý vzduchový sloupec
Vztah mezi \(p_\mathrm{v1}\) a \(p_\mathrm{v2}\)
Pro vztah \(p_\mathrm{v1}\) a \(p_\mathrm{v2}\) platí: \[p_\mathrm{v1}=p_\mathrm{v2}+\rho gl_\mathrm{Hg} ,\tag{1}\] kde \(\rho\) je hustota rtuti a \(g\) je tíhové zrychlení.
Od obou stran rovnice (1) odečteme \(p_\mathrm{v2}\) a dostáváme: \[p_\mathrm{v1}-p_\mathrm{v2}=\rho gl_\mathrm{Hg}.\tag{2}\]
Boyleův-Mariottův zákon
Využijeme Boyleův-Mariottův zákon, který říká, že součin tlaku a objemu ideálního plynu je při stálé teplotě konstantní.
Zformulujeme ho pro vzduchový sloupec \(A\): \[p_\mathrm{v1}V_\mathrm{Av}=p_\mathrm{h}V_\mathrm{Ah},\tag{3}\] kde \(V_\mathrm{Av}\) je objem vzduchového sloupce \(A\), když je kapilára ve vertikální poloze, a \(V_\mathrm{Ah}\) je objem vzduchového sloupce \(A\), když je kapilára v horizontální poloze.
A pro vzduchový sloupec \(B\): \[p_\mathrm{v2}V_\mathrm{Bv}=p_\mathrm{h}V_\mathrm{Bh},\tag{4}\] kde \(V_\mathrm{Bv}\) je objem vzduchového sloupce \(B\), když je kapilára ve vertikální poloze, a \(V_{Bh}\) je objem vzduchového sloupce \(B\), když je kapilára v horizontální poloze.
Napíšeme vztahy pro objemy \(V_\mathrm{Av}\), \(V_\mathrm{Ah}\), \(V_\mathrm{Bv}\) a \(V_\mathrm{Bh}\): \[V_\mathrm{Av}=Sl_\mathrm{v1} ,\tag{5}\] \[V_\mathrm{Ah}=Sl_\mathrm{h} ,\tag{6}\] \[V_\mathrm{Bv}=Sl_\mathrm{v2} ,\tag{7}\] \[V_\mathrm{Bh}=Sl_\mathrm{h},\tag{8}\] kde \(S\) je obsah podstavy kapiláry.
Do (3) dosadíme (5), (6) a dostaneme: \[p_\mathrm{v1}Sl_\mathrm{v1}=p_\mathrm{h}Sl_\mathrm{h}.\tag{9}\]
Do (4) dosadíme (7), (8) a dostaneme: \[p_\mathrm{v2}Sl_\mathrm{v2}=p_\mathrm{h}Sl_\mathrm{h}.\tag{10}\]
Vyjádření \(p_\mathrm{v1}\) a \(p_\mathrm{v2}\)
Obě strany rovnice (9) vydělíme \(Sl_\mathrm{v1}\) a dostáváme: \[p_\mathrm{v1}=p_\mathrm{h}\frac{l_\mathrm{h}}{l_\mathrm{v1}}.\tag{11}\]
Obě strany rovnice (10) vydělíme \(Sl_\mathrm{v2}\) a dostáváme: \[p_\mathrm{v2}=p_\mathrm{h}\frac{l_\mathrm{h}}{l_\mathrm{v2}}.\tag{12}\]
Vyjádření \( p_\mathrm{h}\)
Po dosazení (11) a (12) do (2) dostaneme: \[p_\mathrm{h}\frac{l_\mathrm{h}}{l_\mathrm{v1}}-p_\mathrm{h}\frac{l_\mathrm{h}}{l_\mathrm{v2}}=\rho gl_\mathrm{Hg}.\]
Vytkneme \(p_\mathrm{h}l_\mathrm{h}\): \[p_\mathrm{h}l_\mathrm{h}\left(\frac{1}{l_\mathrm{v1}}-\frac{1}{l_\mathrm{v2}}\right)=\rho gl_\mathrm{Hg}.\]
Zlomek \(\frac{1}{l_\mathrm{v1}} − \frac{1}{l_\mathrm{v2}}\) převedeme na společného jmenovatele: \[p_\mathrm{h}l_\mathrm{h}\left(\frac{l_\mathrm{v2}-l_\mathrm{v1}}{l_\mathrm{v1}l_\mathrm{v2}}\right)=\rho gl_\mathrm{Hg}.\]
Obě strany rovnice upravíme tak, že je vydělíme \(l_\mathrm{h}\left(\frac{l_\mathrm{v2}−l_{v1}}{l_\mathrm{v1}l_\mathrm{v2}}\right) \): \[p_\mathrm{h}=\rho gl_\mathrm{Hg}\frac{l_\mathrm{v2}l_\mathrm{v1}}{l_\mathrm{h}\left(l_\mathrm{v2}-l_\mathrm{v1}\right)}.\tag{13}\]
Číselné řešení
Ze zadání víme: \(l_\mathrm{Hg}=0{,}1\,\mathrm{m}\), \(l_\mathrm{h}=0{,}2\,\mathrm{m}\), \(l_\mathrm{v1}=0{,}15\,\mathrm{m}\) a \(l_\mathrm{v2}=0{,}25\,\mathrm{m}\).
V tabulkách dohledáme tíhové zrychlení \(g\) a hustotu rtuti \(\rho\) : \[g\dot=9{,}81\,\mathrm{\frac{m}{s^2}},\] \[\rho\dot=13 600\mathrm{\frac{kg}{m^3}}.\]
Dosadíme do (13): \[ \begin{eqnarray} p_\mathrm{h} & = & 13600{\cdot}9{,}81{\cdot}0{,}1{\cdot} \frac{0{,}25{\cdot}0{,}15}{0{,}2\left(0{,}25-0{,}15\right)} \mathrm{\frac{kg}{m^3}}{\cdot}\,\mathrm{\frac{m}{s^2}}{\cdot}\,\mathrm{m}{\cdot} \frac{\,\mathrm{m}{\cdot}\,\mathrm{m}}{\,\mathrm{m}\left(\,\mathrm{m}\right)}\\ & = & 25015{,}5\mathrm{\frac{kg}{m}}{\cdot}\,\mathrm{\frac{1}{s^2}} =25 015{,}5\,\mathrm{Pa}\dot=25\,\mathrm{kPa}.\\ \end{eqnarray} \]
Odpověď
Když je kapilára horizontálně, tak tlak vzduchu v ní je \(p_\mathrm{h}=\rho gl_\mathrm{Hg}\frac{l_\mathrm{v2}l_\mathrm{v1}}{l_\mathrm{h}\left(l_\mathrm{v2}-l_\mathrm{v1}\right)}\). Pro zadané hodnoty pak dostáváme \(p_\mathrm{h}\dot=25\,\mathrm{kPa}\).



