Raketa
Úloha číslo: 2311
Raketa o hmotnosti \(M_\mathrm{r}=2\,\mathrm{t}\) s náplní paliva \(M_\mathrm{p}=12\,\mathrm{t}\) je poháněna raketovým motorem s výtokovou rychlostí \(v_\mathrm{R}=5000\,\mathrm{km\cdot h^{-1}}\). Jaká je maximální možná sekundová spotřeba paliva, doba činnosti motoru při této spotřebě a maximální (konečná) rychlost rakety?
Nejvyšší povolené zrychlení posádky je \(7\,\mathrm{g}\).
Zápis
\(M_\mathrm{r}=2\,\mathrm{t}\) … hmotnost samotné rakety
\(M_\mathrm{p}=12\,\mathrm{t}\) … hmotnost paliva
\(v_\mathrm{R} = 5000\,\mathrm{km\cdot h^{-1}}\) … výtoková rychlost paliva
\(a_\mathrm{max}=7g\) … maximální zrychlení
\(\left|\frac{dm}{dt}\right|_\mathrm{max}= ? \,\mathrm{kg\cdot s^{-1}}\) … maximální možná sekundová spotřeba paliva
\(\tau= ? \,\mathrm{s}\) … doba činnosti motoru
\(v_\mathrm{max}= ? \,\mathrm{km\cdot h^{-1}}\) … maximální (konečná) rychlost rakety
Teorie
Pohyb rakety odvodíme v několika krocích. Nejprve uvažujme raketu v izolovaném systému, tzn. uvažujeme, že se v našem systému nachází pouze raketa a nepůsobí na ni žádné vnější síly, nenachází se v působišti silového pole. Vzhledem k inerciálnímu systému se bude raketa pohybovat rychlostí \(\vec v\). Aby raketa mohla zrychlovat, musí vystřelovat palivo (spálené plyny). Řekněme, že vystřelí \(\mathrm{d}m\) spálených plynů za interval \(\mathrm{d}t\) a rychlost těchto spalin vzhledem k našemu izolovanému systému je \(\vec {v_\mathrm{p}}\). Tím získá raketa přírůstek rychlosti \(\mathrm{d}\vec v\).
Rychlost vystřelovaných spálených plynů v našem systému získáme složením rychlosti rakety \(\vec v\) a rychlosti \(\vec {v_\mathrm{R}}\), kterou se pohybují spálené plyny vzhledem k raketě, tj. \(\vec {v_\mathrm{p}}=\vec v + \vec{v_\mathrm{R}}\). Rychlost \(\vec {v_\mathrm{R}}\) nazveme výtokovou rychlostí.
V našem izolovaném systému platí zákon zachování hybnosti (ZZH), který můžeme zapsat následujícím způsobem:
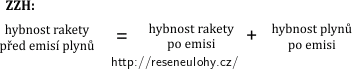
Situace pohybu rakety je nastíněna na obrázku níže, kde vidíme situaci v počátečním čase \(t\) a také situaci po uplynutí doby \(\mathrm{d}t\), tedy po vystřelení paliva o hmotnosti \(\mathrm{d}m\).
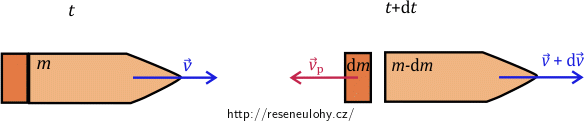
ZZH můžeme pro raketu v izolované soustavě zapsat jako
\[m\vec v = \left(m-|\mathrm{d}m|\right)\left(\vec v + \mathrm{d}\vec v\right) + |\mathrm{d}m|\vec{v_\mathrm{p}}.\]
Uvažujme nyní pohyb rakety v gravitačním poli, kdy gravitační síla působí proti směru startu rakety. Zde je třeba využít tzv. Meščerského rovnici.
Chceme-li rovnici odvodit, vyjdeme z toho, že změna hybnosti se rovná impulsu působící síly:
\[\vec p (t+\mathrm{d}t) - \vec p (t) = \vec F \mathrm{d}t,\] \[\left(m-|\mathrm{d}m|\right)\left(\vec v + \mathrm{d}\vec v\right) + |\mathrm{d}m|\vec{v_\mathrm{p}} - m\vec v = \vec F \mathrm{d}t.\]Po úpravě a zanedbání členu \(\mathrm{d}m \mathrm{d}\vec v\) dostáváme
\[m\mathrm{d}\vec v + |\mathrm{d}m|(\vec{v_\mathrm{p}} - \vec v) = \vec F \mathrm{d}t.\]Rovnici vydělíme \(\mathrm{d}t\), odstraníme absolutní hodnotu u \(\mathrm{d}m\), za rozdíl rychlostí \(\vec{v_\mathrm{p}} - \vec v\) dosadíme výtokovou rychlost a dostáváme Meščerského rovnici:
\[m\frac{\mathrm{d}\vec v}{\mathrm{d}t}=\vec F + \vec {v_\mathrm{R}}\frac{\mathrm{d}m}{\mathrm{d}t},\]
kde \(\vec F\) je síla působící na těleso v daném silovém poli. V našem případě to je gravitační síla působící na raketu. Dosadíme vztah pro gravitační sílu \(\vec F=m\vec g\) do Meščerského rovnice:
\[m\frac{\mathrm{d}\vec v}{\mathrm{d}t}=m\vec g + \vec {v_\mathrm{R}}\frac{\mathrm{d}m}{\mathrm{d}t}.\]
Víme, že gravitační síla působí proti směru pohybu rakety. Stejně tak směr rychlosti vystřelujících spalin plynu je opačný než směr pohybu rakety. Volíme kladný směr ve směru pohybu rakety a rovnici přepíšeme skalárně:
\[m\frac{\mathrm{d}v}{\mathrm{d}t}=-mg - {v_\mathrm{R}}\frac{\mathrm{d}m}{\mathrm{d}t}.\tag{1}\]
Nyní je naším cílem najít vztah pro rychlost rakety \(v\).
Rozšíříme rovnici (1) výrazem \(\mathrm{d}t\):
\[m\mathrm{d}v = -mg\mathrm{d}t - v_\mathrm{R}\mathrm{d}m.\]Vydělíme \(m\) a pro velice malou změnu rychlosti rakety získáváme vztah
\[\mathrm{d}v= -v_\mathrm{R}\frac{\mathrm{d}m}{m} - g\mathrm{d}t. \tag{2}\]
Abychom určili konečnou rychlost rakety \(v_\mathrm{max}\), je potřeba vysčítat (integrovat) rychlosti přes celou dobu činnosti motoru. Motor je v činnosti od času 0 do času, který označíme \(\tau\). Rychlost rakety se za dobu činnosti motoru změní z počáteční rychlosti \(v_0\) na maximální a konečnou rychlost rakety \(v_\mathrm{max}\). Hmotnost rakety se z počáteční hodnoty \(m\), která označuje hmotnost paliva společně s hmotností rakety, změní na konečnou hmotnost samotné rakety, označme ji \(m_\mathrm{k}\).
Z rovnice (2) tedy dostáváme:
\[\int_{v_0}^{v_\mathrm{max}}1\,\mathrm{d}v=-v_\mathrm{R}\,\int_m^{m_\mathrm{k}}{\frac{1}{m}}\,\mathrm{d}m -g\int_0^{\tau}1\,\mathrm{d}t,\]
\[[v]_{v_0}^{v_\mathrm{max}}=-v_\mathrm{R} [\ln m]_m^{m_\mathrm{k}}-g[t]_0^{\tau},\]
\[v_\mathrm{max}-v_0=v_\mathrm{R}\ln{\frac{m}{m_\mathrm{k}}}-g\tau.\tag{3}\]
Rovnice, kterou jsme právě získali, se nazývá Ciolkovského rovnice a udává nám vztah pro maximální dosažitelnou rychlost rakety po dané době činnosti motoru v závislosti na hmotnosti paliva a na hmotnosti samotné rakety.
Nápověda I
Vyjděte z Meščerského rovnice a vyjádřete z ní zrychlení rakety. Pro jakou hmotnost rakety bude zrychlení maximální?
Nápověda II
Maximální sekundovou spotřebu paliva již umíte vyjádřit a znáte i hmotnost paliva. Využijte to k vyjádření času, po který bude motor rakety pracovat.
Nápověda III
Pro určení konečné rychlosti rakety vyjděte z Ciolkovského rovnice odvozené v teoretické části.
Řešení
Vyjdeme z rovnice (2) pro malou změnu rychlosti, kterou jsme odvodili v části teorie z Meščerského rovnice:
\[dv=-v_\mathrm{R}\frac{\mathrm{d}m}{m}-g\mathrm{d}t.\]
Ze zadání máme dánu podmínku pro maximální zrychlení. Zrychlení je změna rychlosti za změnu času, úpravou vztahu výše dostáváme:
\[a=\frac{\mathrm{d}v}{\mathrm{d}t}=-\frac{v_\mathrm{R}}{m}\frac{\mathrm{d}m}{\mathrm{d}t}-g.\tag{4}\]
Zde člen \(\frac{\mathrm{d}m}{\mathrm{d}t}\) znamená hmotnost paliva vytřeleného tryskou rakety za sekundu, budeme ji považovat za konstantní. Následující úvahy nás dovedou k určení maximální možné sekundové spotřeby paliva:
Zrychlení \(a\) je největší, je-li hmotnost rakety jako celku (i s palivem) nejmenší. Nejmenší hmotnost má raketa těsně před skončením činnosti motoru, když spálí veškeré palivo a její hmotnost tvoří pouze samotná konstrukce rakety, tedy když \(m=M_\mathrm{r}\).
Maximální zrychlení máme zadáno formou násobků gravitačního zrychlení:
\[a_\mathrm{max}=7g.\]
Označme si zrychlení obecně jako n-násobek gravitačního zrychlení (n je přirozené číslo). Při dosazení příslušné minimální hmotnosti pro dosažení maximálního zrychlení platí podle (4):
\[a=ng=-\frac{v_\mathrm{R}}{M_\mathrm{r}}\frac{\mathrm{d}m}{\mathrm{d}t}-g.\tag{5}\]
Chceme určit příslušnou maximální možnou sekundovou spotřebu paliva, tedy hodnotu \(\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_\mathrm{max}\). Vyjádřením z rovnice (5) získáváme:
\[\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_\mathrm{max}= -\left(n+1\right)g\frac{M_\mathrm{r}}{v_\mathrm{R}}.\]
Palivo s časem ubývá, tj. hodnota \(\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_\mathrm{max}\) je záporná. Při číselném dosazení budeme pracovat s absolutní hodnotou:
\[\left|\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_\mathrm{max}\right|=\left(7+1\right)\cdot9{,}81\cdot\frac{2000}{1388{,}89}\,\mathrm{kg\cdot s^{-1}}=113{,}0\,\mathrm{kg\cdot s^{-1}}.\]
Nyní známe množství paliva, které se spotřebuje za \(1\,\mathrm{s}\) činnosti motoru. Chceme-li určit celkovou dobu \(\tau\), po kterou je motor v činnosti, stačí celkovou hmotnost paliva vydělit získanou sekundovou spotřebou. Tedy:
\[\tau = \frac{M_\mathrm{p}}{\left|\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_\mathrm{max}\right|}=\frac{M_\mathrm{p}v_\mathrm{R}}{(n+1)gM_\mathrm{r}}.\]
Po číselném dosazení dostáváme:
\[\tau =\frac{12000{\cdot} 1388{,}89}{(7+1)\cdot 9{,}81{\cdot} 2000}\,\mathrm {s}=106{,}2\,\mathrm{s}.\]
Tím jsme určili hledanou dobu činnosti motoru. Zbývá určit konečnou rychlost rakety. Odvození vztahu z Meščerského rovnice je podrobně popsáno v sekci teorie. Dosazením do vztahu (3) příslušné hmotnosti dle zadání a dobu činnosti motoru \(\tau\) určenou výše dostaneme:
\[v_\mathrm{max}=v_\mathrm{R}\ln{\frac{M_\mathrm{r} +M_\mathrm{p}}{M_\mathrm{r}}}-g\frac{M_\mathrm{p}v_\mathrm{R}}{(n+1)gM_\mathrm{r}}=v_\mathrm{R}\ln{\frac{M_\mathrm{r} +M_\mathrm{p}}{M_\mathrm{r}}}-\frac{M_\mathrm{p}v_\mathrm{R}}{(n+1)M_\mathrm{r}}.\]
Číselně dosadíme:
\[v_\mathrm{max}= (5000\cdot\ln{\frac{2000 +12000}{2000}}-\frac{12000{\cdot}5000}{(7+1)\cdot 2000})\,\mathrm{km\cdot h^{-1}}\doteq 6000\,\mathrm{km\cdot h^{-1}}.\]
Určili jsme konečnou rychlost rakety a tím jsme získali odpověď i na poslední část otázky.
Odpověď
Maximální možná sekundová spotřeba paliva je obecně dána vztahem
\[\left|\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_\mathrm{max}\right|=\left(n+1\right)g\frac{M_\mathrm{r}}{v_\mathrm{R}}\]
a pro naši raketu je rovna \(113\,\mathrm{kg\cdot s^{-1}}\).
S tímto výkonem bude motor v činnosti po dobu
\[\tau=\frac{M_\mathrm{p}v_\mathrm{R}}{(n+1)gM_\mathrm{r}},\]
což po číselném dosazení činí \(106\,\mathrm{s}\).
Maximální (konečná) rychlost rakety je \(6000\,\mathrm{km\cdot h^{-1}}\), obecně dána vztahem
\[v_\mathrm{max}=v_\mathrm{R}\ln{\frac{M_\mathrm{r} +M_\mathrm{p}}{M_\mathrm{r}}}-\frac{M_\mathrm{p}v_\mathrm{R}}{(n+1)M_\mathrm{r}}.\]




