Závaží na desce
Úloha číslo: 98
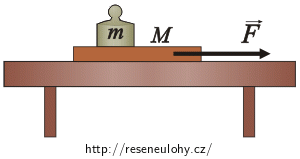
Na stole leží deska o hmotnosti 1 kg a na desce závaží o hmotnosti 2 kg. Jakou minimální konstantní silou musíme vyškubnout desku, aby vyklouzla zpod závaží? Koeficient smykového tření mezi deskou a stolem je f1 = 0,35 a koeficient klidového tření mezi závažím a deskou je f2 = 0,5.
Zápis
M = 1 kg hmotnost desky m = 2 kg hmotnost závaží f1 = 0,35 koeficient tření mezi deskou a stolem f2 = 0,5 koeficient tření mezi závažím a deskou F = ? minimální síla potřebná pro vyškubnutí desky zpod závaží Rozbor
1. Rozmyslíme si, jaká je kritická podmínka pro to, aby deska vyklouzla zpod závaží. Nejprve zatáhneme za desku malou silou F. Závaží se rozjede spolu s deskou. Jaká síla udělila závaží zrychlení při rozjezdu? Závaží se rozjelo díky působení klidové třecí síly mezi ním a deskou. Velikost této třecí síly je rovna
\[F_\mathrm{t_2}\,=\,ma.\]2. Zvětšíme-li sílu, kterou zatáhneme za desku, bude zrychlení, se kterým se rozjede, větší. Aby se s deskou rozjelo i závaží, musí zapůsobit větší třecí síla. Maximální hodnota, které může klidová třecí síla dosáhnout, je
\[F_\mathrm{t_{2_{\,max}}}\,=\,mgf_2.\]Zatáhneme-li za desku takovou silou F, že zrychlení, se kterým se deska začne rozjíždět, je větší než zrychlení, jaké může udělit závaží maximální klidová třecí síla, desku vyškubneme. Pro maximální zrychlení, které můžeme desce se závažím udělit, aby na ní závaží zůstalo, tedy platí:
\[ma_\mathrm{max}\,=\,mgf_2.\]3. Maximální zrychlení, které lze desce udělit, známe. Hledanou sílu pak můžeme vyjádřit, když si rozepíšeme pohybovou rovnici pro desku.
Nápověda 1 – síly působící na desku a závaží
Nakreslete si obrázek a v něm vyznačte všechny síly působící na desku a na závaží.
Nápověda 2 – pohybové rovnice
Napište pohybovou rovnici pro desku a pro závaží a přepište je skalárně.
Nápověda 3 – třecí síly, maximální zrychlení
Uvědomte si, na čem závisí velikost třecí síly působící mezi deskou a podložkou a jak ji můžeme vyjádřit. Jaká je maximální hodnota, které může dosáhnout klidová třecí síla působící mezi závažím a deskou, a jaké jí odpovídá zrychlení?
Nápověda 4 – výpočet síly
Znáte maximální hodnotu zrychlení, které můžete udělit závaží, aby ještě zůstalo na desce. Z pohybové rovnice (7) pro desku můžete zjistit velikost tahové síly, která tomuto zrychlení odpovídá. Zatáhnete-li silou větší, desku vytrhnete.
CELKOVÉ ŘEŠENÍ
Nakreslíme do obrázku všechny síly, které působí na desku a na závaží, a napíšeme pohybové rovnice.
Síly působící na desku M:
\(\vec{F}_\mathrm{G_1}\)…síla tíhová
\(\vec{N}_{1}\)…síla, kterou na desku působí podložka
\(\vec{N}^,_{2}\)…síla, kterou závaží tlačí na desku
\(\vec{F}_\mathrm{t_1}\)…síla třecí mezi stolem a deskou
\(\vec{F}^,_\mathrm{t_2}\)…síla třecí mezi deskou a závažím
\(\vec{F}\)…síla, kterou taháme za desku
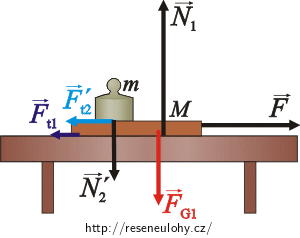
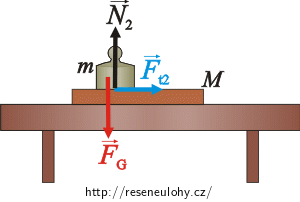
Síly působící na závaží m:
\(\vec{F}_\mathrm{G_2}\)…síla tíhová
\(\vec{N}_{2}\)…síla, kterou deska tlačí na závaží
\(\vec{F}_\mathrm{t_2}\)…síla třecí mezi deskou a závažím
Pohybová rovnice pro desku:
\[\vec{F}_\mathrm{t_1}+\vec{F}^,_\mathrm{t_2}+\vec{F}+\vec{F}_\mathrm{G_1}+\vec{N}_1+\vec{N}^,_{2}\,=\,M\vec{a}.\tag{1}\]Nyní přepíšeme rovnici (1) skalárně, osu x orientujeme ve směru pohybu, osa y je na osu x kolmá:
\[x:\qquad -F_\mathrm{t_1}-F^,_\mathrm{t_{2}}+F\,=\,Ma,\tag{2}\] \[y:\qquad N_1-N_2^,-F_\mathrm{G_1}\,=\,0.\tag{3}\]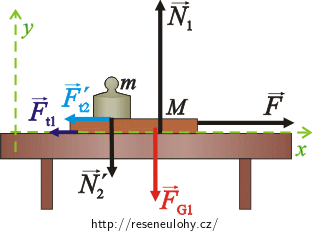
Pohybová rovnice pro závaží:
\[\vec{F}_\mathrm{t_2}+\vec{F}_\mathrm{G_2}+\vec{N}_2\,=\,m\vec{a}.\tag{4}\]Deska i závaží se pohybují se stejným zrychlením.
Nyní přepíšeme rovnici (4) skalárně, osu x orientujeme ve směru pohybu, osa y je na osu x kolmá:
\[x:\qquad F_\mathrm{t_2}\,=\,ma,\tag{5}\] \[y:\qquad N_2-F_\mathrm{G_2}\,=\,0.\tag{6}\]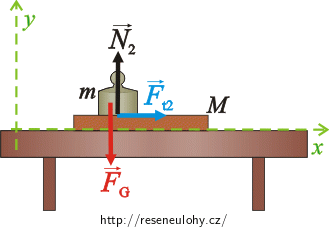
Deska působí silou \(\vec{N}_2\) na závaží a závaží působí silou \(\vec{N}^,_{2}\) na desku. Stejně tomu je se silami \(\vec{F}_\mathrm{t_2}\) a \(\vec{F}^,_\mathrm{t_2}\). Podle 3. Newtonova zákona platí pro velikosti sil:
\[\left|\vec{N}_2\right|\,=\,\left|\vec{N}^,_{2}\right|,\] \[\left|\vec{F}_\mathrm{t_2}\right|\,=\,\left|\vec{F}^,_\mathrm{t_2}\right|.\]Rovnice (2) a (3) můžeme přepsat:
\[-F_\mathrm{t_1}-F_\mathrm{t_2}+F\,=\,Ma,\tag{7}\] \[F_\mathrm{G_1}-N_1+N_2\,=\,0.\tag{8}\]Třecí síly:
Třecí síla působící na desku je úměrná tlakové síle, kterou deska působí na stůl. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí stůl na desku. Podobně maximální klidová třecí síla působící na závaží je úměrná tlakové síle, kterou závaží působí na desku. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí deska na závaží. Zapíšeme to rovnicemi:
\[F_\mathrm{t_1}\,=\,f_1N_1,\] \[F_\mathrm{t_{2_{\,max}}}\,=\,f_2N_2.\]Síly N1 a N2 vyjádříme z rovnic (6) a (8):
\[N_2\,=\,F_\mathrm{G_2},\] \[N_1\,=\,F_\mathrm{G_1}+N_2\,=\,F_\mathrm{G_1}+F_\mathrm{G_2}.\]Pro třecí síly platí:
\[F_\mathrm{t_1}\,=\,f_1F_\mathrm{G_1}+f_1F_\mathrm{G_2}\,=\,f_1Mg+f_1mg\,=\,(M+m)gf_1,\] \[F_\mathrm{t_2{max}}\,=\,f_2mg.\]Maximální zrychlení, které může klidová třecí síla závaží udělit, je rovno:
\[F_\mathrm{t_{2_{\,max}}}\,=\,mgf_2\,=\,ma_\mathrm{max},\] \[a_\mathrm{max}\,=\,gf_2.\tag{9}\]Dosadíme za maximální hodnotu zrychlení do rovnice (7):
\[F-F_\mathrm{t_1}-F_\mathrm{t_2}\,=\,Ma_\mathrm{max}.\]Dosadíme ještě za třecí síly:
\[F\,-\,\left(M+m\right)gf_1\,-\,mgf_2\,=\,Mgf_2.\]Vyjádříme sílu F:
\[F\,=\,\left(M+m\right)gf_1\,+\,\left(M+m\right)gf_2,\] \[F\,=\,\left(M+m\right)g\left(f_1+f_2\right).\tag{10}\]Dosadíme číselně:
\[F\,=\,(1 + 2)\,\cdot9{,}81\,\cdot(0{,}35 + 0{,}5)\,\textrm{N},\] \[F \,\dot=\, 25 \,\textrm{N}.\]CELKOVÁ ODPOVĚĎ
Desku musíme vyškubnout minimální konstantní silou \(F\,=\,\left(M+m\right)g\left(f_1+f_2\right)\,\dot=\, 25 \,\textrm{N}\), aby vyklouzla zpod závaží.





