Auto na mostě
Úloha číslo: 231
Auto o hmotnosti 1200 kg přejíždí most vypuklého tvaru. Jak velkou silou působí na most v jeho nejvyšším bodě, přejíždí-li ho rychlostí 54 km·h−1? Poloměr křivosti mostu je 45 m.
Řešte z hlediska inerciálního i neinerciálního systému.
Zápis
m = 1200 kg hmotnost auta v = 54 km·h−1 rychlost auta r = 45 m poloměr křivosti mostu F = ? (N) síla, kterou působí auto na most v jeho nejvyšším bodě Nápověda 1 - inerciální systém: síly
Řešme úlohu nejdříve z hlediska inerciálního systému spojeného se zemí: Jaké síly na auto v nejvyšším bodě mostu působí? Nakreslete si obrázek.
Nápověda 2 - inerciální systém: druh pohybu
Po jaké trajektorii se auto pohybuje? Čím je takový pohyb z hlediska sil charakterizován? Co z toho můžete vyvodit pro výslednici dvou výše uvedených sil a její velikost?
Nápověda 3 - inerciální systém: velikost síly F
Ze získaného vztahu vyjádřete velikost hledané síly F. Pro její určení potřebujete znát velikost tíhové a dostředivé síly. Umíte je vypočítat?
Nápověda 4 - pro řešení v neinerciálním systému
Nyní vyřešíme problém z hlediska neinerciálního systému spojeného s autem. Tento systém se rovnoměrně otáčí kolem středu kružnice, po jejíž části auto jede. Auto je v tomto systému v klidu. Jaké síly zde na auto působí a co platí pro jejich výslednici?
Nápověda 5 - pro řešení v neinerciálním systému
Podobně jako při počítání v inerciálním systému si vzpomeňte na vztahy pro tíhovou a odstředivou sílu a vypočítejte velikost síly F.
Celkové řešení
Z hlediska inerciálního systému spojeného se zemí:
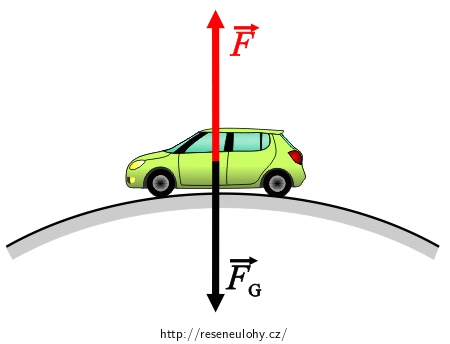
Na auto působí v nejvyšším bodě mostu dvě síly:
a) tíhová síla \(\vec{F}_\mathrm{G}\) kolmo dolů,
b) tlaková síla mostu \(\vec{F}\). Touto silou působí most svisle vzhůru na auto a podle 3. Newtonova zákona působí stejně velkou silou i auto svisle dolů na most. Právě velikost této síly chceme vypočítat.
Poznámka: Tlaková síla mostu je ve skutečnosti rozložena na všechna čtyři kola. V obrázku je nahrazena výslednicí působící v těžišti auta.
Most má tvar části kružnice, auto se tedy pohybuje po části kružnice. Takový pohyb je charakterizován nějakou dostředivou silou \(\vec{F}_\mathrm{d}\), která míří do středu opisované kružnice a zakřivuje trajektorii auta.
Dostředivá síla není žádným novým typem síly, její roli zastupují v různých situacích síly jiné, nám dobře známé (tíhová, třecí apod.). V naší úloze je dostředivou silou výslednice sil \(\vec{F_\mathrm{G}}\) a \(\vec{F}\), tedy:
\[\vec{F}_\mathrm{d}\,=\,\vec{F_\mathrm{G}}\,+\,\vec{F}.\]Protože síly \(\vec{F_\mathrm{G}}\) a \(\vec{F}\) mají opačný směr, lze pro velikost této výslednice psát:
\[F_\mathrm{d}\,=\,F_\mathrm{G}\,-\,F.\]Tedy:
\[F\,=\,F_\mathrm{G}\,-\,F_\mathrm{d}.\tag{1}\]Použijeme vztahy pro velikost tíhové a dostředivé síly:
\[F_\mathrm{G}\,=\,mg\,,\] \[F_\mathrm{d}\,=\,ma_\mathrm{d}\,=\, m\frac{v^2}{r}\,,\]kde m je hmotnost auta, g tíhové zrychlení, v rychlost auta a r poloměr opisované (části) kružnice.
Po dosazení do vztahu (1) tak dostáváme výsledný vzorec pro hledanou sílu F: \[F\,=\,mg\,-\,m\frac{v^2}{r}\,=\,m(g\,-\,\frac{v^2}{r}).\]Číselně:
\[m\,=\,1\,200\,\mathrm{kg},\] \[g\,=\,9{,}81\,\mathrm{m{\cdot}s^{-2}},\] \[v\,=\,54\,\mathrm{km{\cdot}h^{-1}}\,=\,15\,\mathrm{m{\cdot}s^{-1}},\] \[r\,=\,45\,\mathrm{m},\] \[F\,=\,m(g\,-\,\frac{v^2}{r})\,=\,(1200{\cdot}(9{,}81\,-\,\frac{15^2}{45}))\,\mathrm{N}\,=\,5772\,\mathrm{N}.\]Z hlediska otáčejícího se neinerciálního systému spojeného s autem:
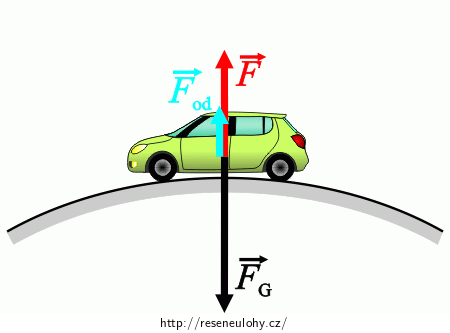
Na auto působí v nejvyšším bodě mostu z hlediska našeho neinerciálního systému tři síly:
a) Tíhová síla \(\vec{F_\mathrm{G}}\) kolmo dolů.
b) Tlaková síla mostu \(\vec{F}\). Touto silou působí most svisle vzhůru na auto a podle 3. Newtonova zákona působí stejně velkou silou i auto svisle dolů na most. Právě velikost této síly chceme vypočítat.
c) Setrvačná odstředivá síla \(\vec{F}_\mathrm{od}\), která míří od středu otáčení neinerciálního systému, v nejvyšším bodě mostu tedy svisle vzhůru.
Protože auto je z hlediska tohoto systému v klidu, musí být dle 1. Newtonova zákona výslednice sil na něj působících nulová (nulový vektor):
\[\vec{F_\mathrm{G}}\,+\,\vec{F}\,+\,\vec{F}_\mathrm{od}\,=\,\vec{o}.\]Tíhová síla má opačný směr než zbylé dvě síly, pro jejich velikosti lze psát:
\[F_\mathrm{G}\,-\,F\,-\,F_\mathrm{od}\,=\,0.\]Tedy:
\[F\,=\,F_\mathrm{G}\,-\,F_\mathrm{od}.\tag{2}\]Připomeňme si vztahy pro velikost tíhové a setrvačné odstředivé síly (velikost setrvačné odstředivé síly je zde rovna velikosti dostředivé síly z hlediska inerciálního systému):
\[F_\mathrm{G}\,=\,mg\,,\] \[F_\mathrm{od}\,=\,m\frac{v^2}{r}\,,\]kde m je hmotnost auta, g tíhové zrychlení, v rychlost auta a r poloměr opisované (části) kružnice.
Po dosazení do vztahu (2) tak dostáváme výsledný vzorec pro hledanou sílu F:
\[F\,=\,mg\,-\,m\frac{v^2}{r}\,=\,m(g\,-\,\frac{v^2}{r}),\]což je vztah, ke kterému jsme dospěli i při výpočtu z hlediska inerciálního systému — oběma postupy jsme tedy získali stejný výsledek.
Výsledek
Auto působí na most silou \(F\,=\,m(g\,-\,\frac{v^2}{r})\,=\,5772\,\mathrm{N}\).
Komentář
V úloze jsme počítali, jak velkou silou působí auto na most vypuklého tvaru, tedy tíhu auta. Zjistili jsme, že tíha auta je v dané situaci menší, než kdyby auto jelo po vodorovném mostě. V tom případě by síla, kterou tlačí na most (tedy jeho tíha), byla rovna \(F_\mathrm{G}\,=\,mg\,\).
Můžete si zkusit spočítat, při jak velké rychlosti by auto přestalo na náš vypuklý most tlačit úplně a jeho tíha by byla tedy nulová.
Rovněž si můžete spočítat, jak velkou silou by auto tlačilo do mostu, který by byl zakřivený opačně (dolík) a měl stejný poloměr křivosti.




