Síly v laně
Úloha číslo: 222
Těleso o hmotnosti 20 kg je uvázáno na laně a rotuje ve svislé rovině. Poloměr rotace je 1 m.
Jaká je maximální a minimální síla působící v laně při rychlosti tělesa 10 m·s−1?
Úlohu řešte z pohledu inerciálního pozorovatele stojícího na zemi i neinerciálního pozorovatele rotujícího spolu s tělesem.
Zápis
m = 20 kg hmotnost tělesa v = 10 m·s−1 obvodová rychlost tělesa r = 1 m poloměr otáčení tělesa Fmax = ? velikost maximální síly působící v laně Fmin = ? velikost minimální síly působící v laně Nápověda 1 – síly z hlediska inerciálního systému
Rozmyslete si, jaké všechny síly působí na těleso z hlediska inerciálního systému spojeného se zemí.
Jaká síla působí v laně?
Rozmyslete si, ve kterých místech trajektorie tělesa bude síla v laně největší a kde nejmenší.
Nápověda 2 – síly z hlediska neinerciálního systému
Rozmyslete si, jaké všechny síly působí na těleso z hlediska neinerciálního systému spojeného s tělesem na laně, jak se těleso vzhledem k tomuto systému pohybuje a co bude platit pro výslednici sil.
Rozmyslete si, ve kterých místech pohybu tělesa bude síla v laně největší a kde nejmenší. Zapište, pohybovou rovnici v těchto bodech.
Celkové řešení
Úlohu lze řešit z hlediska inerciálního nebo neinerciálního vztažného systému.
1. Z hlediska inerciálního vztažného systému spojeného se zemí
Z hlediska inerciálního systému (spojeného se zemí) obíhá těleso po kružnici a působí na ně tíhová síla FG a tahová síla lana FL.
Působí-li lano na těleso tahovou silou FL, působí těleso na lano stejně velkou, opačně orientovanou silou. Co do velikosti je tedy síla v laně rovna FL.
V obrázcích jsou síly působící na těleso nakresleny pro nejvyšší a nejnižší bod trajektorie, kdy obě leží v jedné přímce.
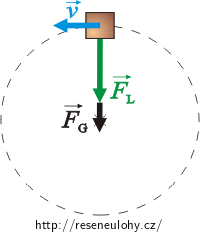
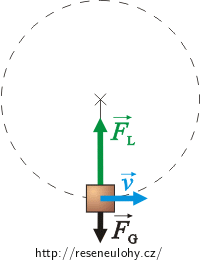
Výslednice sil v těchto bodech uděluje tělesu příslušné dostředivé zrychlení.
Pro velikost sil v nejvyšším bodě platí:
\[F_\mathrm{do}\,=\, F_\mathrm{L} + F_\mathrm{g},\] \[F_\mathrm{L} \,=\, F_\mathrm{do} - F_\mathrm{g} \,=\, m\frac{v^{2}}{r} - mg.\]Pro velikost sil v nejnižším bodě platí:
\[F_\mathrm{do} \,=\, F_\mathrm{L} - F_\mathrm{g},\] \[F_\mathrm{L} \,=\, F_\mathrm{do} + F_\mathrm{g} \,=\, m\frac{v^{2}}{r} + mg.\]Ve vodorovné poloze je tah lana přímo silou dostředivou a je co do velikosti roven:
\[F_\mathrm{L} \,=\, F_\mathrm{do} \,=\, m\frac{v^{2}}{r}.\]Lano bude muset tedy zatáhnout nejvíce v nejnižším bodě, kdy tíhová síla působí v opačném směru. Nejmenší tah bude v bodě nejvyšším, kdy tíhová síla působí ve stejném směru.
Číselně:
Maximální tah – nejnižší bod:
\[F_{\mathrm{max}} \,=\,m\frac{v^{2}}{r}+mg\,=\,20\,\cdot\,\frac{10^{2}}{1}+20\,\cdot\,10\,\mathrm{N}\,= \, 2200\,\mathrm{N}.\]Minimální tah – nejvyšší bod:
\[F_{\mathrm{min}} \,=\, m\frac{v^{2}}{r}-mg\,=\,20\,\cdot\,\frac{10^{2}}{1}-20\,\cdot\,10\,\mathrm{N}\,= \,1800\,\mathrm{N}.\]Za tíhové zrychlení bylo dosazeno 10 m s−2.
1. Z hlediska neinerciálního vztažného systému spojeného s rotujícím tělesem
Díváme-li se na těleso z hlediska neinerciálního systému (spojeného s tělesem na laně), je vzhledem k nám v klidu. Kromě tíhové síly a tahové síly lana na něj působí ještě setrvačná odstředivá síla. Výslednice sil je nulová.
Působí-li lano na těleso tahovou silou FL, působí těleso na lano stejně velkou, opačně orientovanou silou. Co do velikosti je tedy síla v laně rovna FL.
V obrázcích jsou síly působící na těleso nakresleny pro nejvyšší a nejnižší bod trajektorie, kdy leží v jedné přímce.
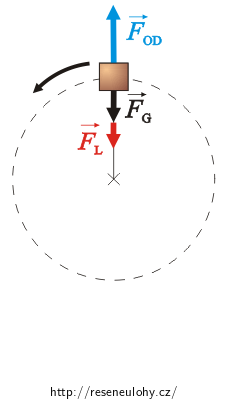
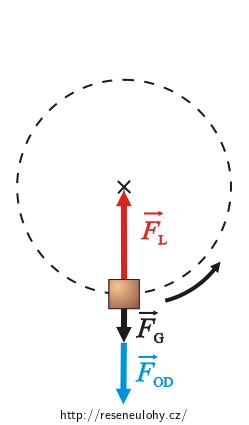
Výslednice sil v těchto bodech je nulová.
Pro velikost sil v nejvyšším bodě platí:
\[F_\mathrm{od} - F_\mathrm{L} - F_\mathrm{g}\,=\,0,\] \[F_\mathrm{L} \,=\, F_\mathrm{od} - F_\mathrm{g} \,=\, m\frac{v^{2}}{r} - mg.\]Pro velikost sil v nejnižším bodě platí:
\[F_\mathrm{L} - F_\mathrm{od} - F_\mathrm{g} \,=\,0,\] \[F_\mathrm{L} \,=\, F_\mathrm{od} + F_\mathrm{g} \,=\, m\frac{v^{2}}{r} + mg.\]Ve vodorovné poloze je tah lana roven co do velikosti setrvačné odstředivé síle:
\[F_\mathrm{L} = F_\mathrm{od} \,=\, m\frac{v^{2}}{r}.\]Lano bude muset tedy zatáhnout nejvíce v nejnižším bodě, nejmenší tah bude v bodě nejvyšším.
Číselně:
Maximální tah – nejnižší bod:
\[F_{\mathrm{max}} \,=\,m\frac{v^{2}}{r}+mg\,=\,20\,\cdot\,\frac{10^{2}}{1}+20\,\cdot\,10\,\mathrm{N}\,= \, 2200\,\mathrm{N}.\]Minimální tah – nejvyšší bod:
\[F_{\mathrm{min}} \,=\, m\frac{v^{2}}{r}-mg\,=\,20\,\cdot\,\frac{10^{2}}{1}-20\,\cdot\,10\,\mathrm{N}\,= \,1800\,\mathrm{N}.\]Za tíhové zrychlení bylo dosazeno 10 m·s−2.
Odpověď
\[F_{\mathrm{max}} \,=\,m\frac{v^{2}}{r}+mg\,=\, 2200\,\mathrm{N}\] \[F_{\mathrm{min}} \,=\,m\frac{v^{2}}{r}-mg\,=\,1800\,\mathrm{N}\]Za tíhové zrychlení bylo dosazeno 10 m·s−2.
Velikost síly působící v laně nezávisí na tom, ve kterém systému počítáme. Maximální síla v laně je při průchodu tělesa nejnižším bodem a má velikost 2200 N. Minimální síla v laně je při průchodu tělesa nejvyšším bodem a má velikost 1800 N.
Podobná úloha
Tahová síla provazu působícího na kouli rotující ve svislé rovině se počítá z pohledu inerciální vztažné soustavy i v úloze Koule přivázaná na konci provazu.



