Krychle na dně pod vodou
Úloha číslo: 2155
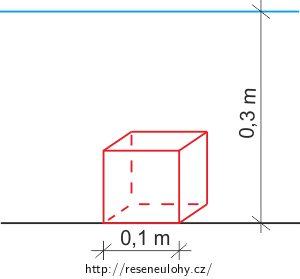
Ocelová krychle o hraně 0,1 m je ponořena do vody až na vodorovné dno v hloubce 0,3 m. Modul pružnosti v tahu je 210 GPa. O kolik se zmenší její objem?
Zápis
a = 0,1 m hrana krychle h = 0,3 m hloubka dna E = 210 GPa modul pružnosti v tahu ΔV = ? změna objemu krychle Rozbor
Nejprve je třeba si uvědomit, že krychle je v rovnováze. Protože se síly působící na libovolný rovinný řez krychle vzájemně vyruší, nedochází nikde v krychli ke smykovému napětí. Zatímco na horní stěně, a tedy i dolní stěně je konstantní tlak, na bočních stěnách se tlak spojitě mění lineárně s hloubkou. Proto je třeba krychli rozdělit na malé krychličky, na kterých bychom mohli uvažovat všechny tlaky konstantní, určit jejich objemové změny a integrací získat celkovou změnu.
Nápověda
Nejprve stanovte průběh hydrostatického tlaku. Krychli rozdělte na malé elementární krychličky a určete pomocí vhodného vzorce jejich objemové změny. Pomocí Hookova zákona tyto změny vyjádřete v závislosti na tlaku. Celková změna objemu krychle je součtem změn objemů všech krychliček. Toho již dosáhnete objemovou integrací přes celou krychli.
Řešení
Na krychli působí pouze tlak, protože všechny tečné složky se v krychli vyruší. Průběh tlaku působícího na krychli podle hydrostatických vztahů znázorňuje obrázek:
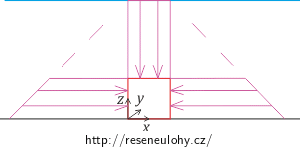
V našem případě můžeme hydrostatický tlak na horní stěnu krychle napsat v souladu se zavedenou soustavou souřadnic na obrázku ve tvaru:
\[p_\mathrm{s}\,=\,\rho g \left(h-a\right).\tag{1}\]Tlak na bočních stěnách krychle je lineární funkcí proměnné z:
\[p_\mathrm{v}\,=\,\rho g \left(h-z\right).\tag{2}\]Protože na bočních stěnách není konstantní tlak, je třeba krychli rozdělit na tak malé krychličky, abychom tlak působící na jejich stěny mohli už uvažovat jako konstantní. Objemovou změnu každé krychličky můžeme napsat vztahem:
\[\mathrm{d}V-\mathrm{d}V_0\,=\,\left(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}\right)\mathrm{d}V_0,\tag{3}\]kde V0 znamená původní objem a symbol ε značí deformaci. Jelikož tlak závisí na z, můžeme (3) přepsat na:
\[\mathrm{d}V-\mathrm{d}V_0\,=\,\left(2\varepsilon_{xx}+\varepsilon_{zz}\right)\mathrm{d}V_0.\tag{4}\]Podle Hookova zákona platí:
\[\varepsilon_{xx}\,=\,-\frac{p_\mathrm{v}}{E}\,=\,-\frac{\rho g \left(h-z\right)}{E},\tag{5}\]a:
\[\varepsilon_{zz}\,=\,-\frac{p_\mathrm{s}}{E}\,=\,-\frac{\rho g \left(h-a\right)}{E},\tag{6}\]Dosazením (5) a (6) do (4) získáme:
\[\mathrm{d}V-\mathrm{d}V_0\,=\,-\frac{\rho g}{E}\left(2\left(h-z\right)+\left(h-a\right)\right)\mathrm{d}V_0\,=\,-\frac{\rho g}{E}\left(3h-2z-a\right)\mathrm{d}V_0.\tag{7}\]Celkovou změnu krychle dostaneme integrálem vztahu (7) přes celý její objem, tedy:
\[\Delta V\,=\,-\frac{\rho g}{E}\int_{0}^{a}\int_{0}^{a}\int_{0}^{a}\left(3h-2z-a\right)\mathrm{d}x\mathrm{d}y\mathrm{d}z.\tag{8}\]Při řešení (8) platí:
\[\Delta V\,=\,-\frac{\rho g a^{2}}{E}\int_{0}^{a}\left(3h-2z-a\right)\mathrm{d}z\,=\,-\frac{\rho g a^{2}}{E}\left(3ha-a^{2}-a^{2}\right).\]Takže z (8) vychází:
\[\Delta V\,=\,-\frac{\rho g a^{3}}{E}\left(3h-2a\right).\tag{9}\]Záporná změna je v souladu s tím, že se jedná o tlak. Nyní už jen do (9) číselně dosadíme:
\[\Delta V\,=\,-\frac{1000{\cdot}9{,}81{\cdot}0{,}1^3}{210{\cdot}10^9}\left(3{\cdot}0{,}3-2{\cdot}0{,}1\right)\mathrm{m^3}\,=\,-3{,}27{\cdot}10^{-11}\mathrm{m^3}.\]Odpověď
Objem krychle se zmenší o:
\[\left|\Delta V\right|\,=\,3{,}27{\cdot}10^{-11}\mathrm{m^3}.\]

