Vodorovně zavěšená tyč
Úloha číslo: 2092
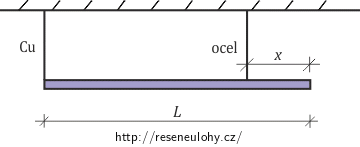
Tuhá vodorovná zavěšená tyč všude stejného průřezu délky 1,2 m a hmotnosti 60 kg je nesena dvěma dráty, ocelovým a měděným. Oba dráty jsou stejně dlouhé a mají stejný průřez. Měděný drát je připojen k jednomu konci tyče a ocelový drát je ve vzdálenosti x od druhého konce tak, že oba dráty jsou protaženy o stejnou délku. Určete síly, jimiž působí tyč na jednotlivé dráty, a určete vzdálenost x.
Zápis
L = 1,20 m délka tyče m = 60 kg hmotnost tyče Z tabulek:
E1 = 125·103 MPa Youngův modul pružnosti v tahu měděného drátu E2 = 220·103 MPa Youngův modul pružnosti v tahu ocelového drátu g = 9,81 ms-2 tíhové zrychlení F1 = ? N síla působící na měděný drát F2 = ? N síla působící na ocelový drát x = ? m vzdálenost od konce tyče Rozbor
V úloze je potřeba určit tři neznámé, k řešení budou zapotřebí tři (lineárně nezavislé) rovnice.
Tyč visí v klidu, musí být tedy splněny podmínky rovnováhy. To znamená, že výslednice sil a výslednice momentů sil působících na tyč jsou rovny nule. Rozepsáním těchto podmínek získáme dvě rovnice pro hledané neznámé.
Dále víme, že oba dráty mají stejné průřezy, stejnou délku a protáhnou se o stejnou délku. Budeme uvažovat pružnou deformaci a z Hookova zákona vyjádříme relativní prodloužení drátů. Z jejich rovnosti pak získáme třetí potřebnou rovnici.
Nápověda 1 – podmínky rovnováhy
Vyznačte si do obrázku, jaké síly působí na tyč. Tyč je v klidu, proto musí být splněny podmínky rovnováhy sil a momentů sil. Zapište si je a obě rozepište skalárně.
Nápověda 2 – relativní prodloužení drátů
Oba dráty mají podle zadání stejnou délku a průřez a při zavěšení tyče se protáhnou stejně. Uvažujte pružnou deformaci. Pomocí Hookova zákona si vyjádřete relativní prodloužení obou drátů a dejte je do rovnosti.
Řešení
Na obrázku jsou vyznačeny síly působící na tyč:
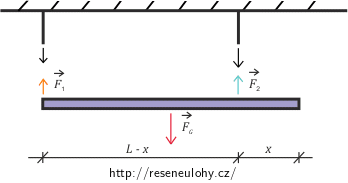
Soustava je v rovnováze, platí tedy, že výslednice sil působících na tyč je rovna nule:
\[\sum \vec{F}^\, =\,0.\]To samé platí pro momenty sil:
\[\sum \vec{M}^\, =\,0.\]Obě podmínky rovnováhy přepíšeme ve skalárním tvaru. Pro síly získáme rovnici:
\[F_1+F_2\,=\,mg.\tag{1}\]Momenty sil budeme vztahovat k levému konci tyče. Pak platí:
\[\left(L-x\right)F_2\,=\,\frac{L}{2}mg.\tag{2}\]Uvažujeme pružnou deformaci drátů. Pomocí Hookova zákona vyjádříme jejich relativní prodloužení:
\[\frac{\Delta l}{l}\, =\,\frac{1}{E}\frac{F}{S}.\tag{3}\]Průřezy, délky a změny délek obou drátů jsou podle zadání stejné. Z (3) proto získáváme:
\[\frac{F_1}{E_1}\, =\,\frac{F_2}{E_2}.\]Odtud:
\[F_1\, =\,\frac{E_1}{E_2}F_2.\tag{4}\]Rovnice (1) a (4) nám dávají dvě rovnice o dvou neznámých. Vyjádřením F2 v (1) a dosazením do (4) máme:
\[F_1\, =\,\frac{E_1}{E_2}\left(mg-F_1\right).\]Z toho již vyjádříme sílu působící na měděný drát:
\[F_1\, =\,\frac{E_1}{E_1+E_2}mg.\tag{5}\]Dosazením z (5) do (4) pak dostaneme sílu působící na ocelový drát:
\[F_2\, =\,\frac{E_2}{E_1+E_2}mg.\tag{6}\]Číselným dosazením do (5) a (6) již určíme hledané velikosti sil:
\[F_1\, =\,\frac{125{\cdot}10^{12}}{125{\cdot}10^{12}+220{\cdot}10^{12}}\cdot60{\cdot}9{,}81\,\mathrm{N}=\,213{,}261\,\mathrm{N}\,\dot= \,213{,}3\,\mathrm{N}\]a
\[F_2\, =\,\frac{220{\cdot}10^{12}}{125{\cdot}10^{12}+220{\cdot}10^{12}}\cdot60{\cdot}9{,}81\,\mathrm{N}=\,375{,}339\,\mathrm{N}\,\dot= \,375{,}3\,\mathrm{N}.\]Pro druhou část úlohy nejprve upravíme tvar (2) na:
\[F_2 x\,=\, F_2 L - \frac{L}{2}mg.\]Odtud:
\[x\,=\,L\left(1-\frac{mg}{2F_2}\right).\tag{7}\]K výpočtu x stačí již dosadit (6) do (7):
\[x\,=\,L\left(1-\frac{E_1 + E_2}{2E_2}\right),\] \[x\,=\,\frac{L}{2}\left(1-\frac{E_1}{E_2}\right).\tag{8}\]Na závěr už jen číselně dosadíme do (8):
\[x\,=\,\frac{1{,}2}{2}\cdot\left(1-\frac{125{\cdot}10^{12}}{220{\cdot}10^{12}}\right)\,\mathrm{m}=\,0{,}259\,\mathrm{m}\,\dot= \,0{,}26\,\mathrm{m}.\]Odpoveď
Tahová síla působící na měděný drát je:
\[F_1\, =\,\frac{E_1}{E_1+E_2}mg\,\dot= \,213{,}3\,\mathrm{N}.\]Na ocelový drát:
\[F_2\, =\,\frac{E_2}{E_1+E_2}mg\,\dot= \,375{,}3\,\mathrm{N}.\]Vzdálenost připojení ocelového drátu od druhého konce tyče je:
\[x\,=\,\frac{L}{2}\left(1-\frac{E_1}{E_2}\right)\,\dot= \,0{,}26\,\mathrm{m}.\]



