Kostka ledu a časově proměnlivá síla
Úloha číslo: 80
Na kostku ledu o hmotnosti 10 kg působí ve vodorovném směru síla, která závisí na čase podle vztahu Fx = p(q − t) , kde p = 100 N·s−1, q = 1 s. V čase t = 0 s byla kostka ledu v počátku souřadné soustavy a měla velikost rychlosti 0,2 m·s−1 a síla směr rychlosti. Kostka ledu se pohybuje po vodorovné ledové ploše bez tření.
Určete, kdy a kde se kostka ledu zastaví.
Poznámka: Pod rychlostí a zrychlením máme dále na mysli jejich velikost.
Zápis
m = 10 kg hmotnost kostky ledu Fx = p(q − t) síla působící na kostku p = 100 N·s−1 konstanta q = 1 s−1 konstanta v0 = 0,2 m·s−1 počáteční rychlost kostky tz = ? čas zastavení kostky xz = ? dráha zastavení kostky Nápověda 1 – zrychlení kostky ledu
Uvědomte si, jaké síly působí na kostku ledu. Napište pro ni pohybovou rovnici a vyjádřete z ní zrychlení.
Nápověda 2 – závislost rychlosti a dráhy na čase
Ve vztahu (2) jste získali zrychlení. Integrací zrychlení dostanete rychlost a integrací rychlosti dráhu.
Nápověda 3 – čas zastavení
Uvědomte si, jaká bude rychlost kostky ledu v okamžiku zastavení.
Nápověda 4 – dráha zastavení
Známe čas zastavení a také závislost uražené dráhy na čase. Dráhu zastavení spočítáme dosazením času zastavení do tohoto vztahu.
CELKOVÉ ŘEŠENÍ
Do obrázku nakreslíme síly působící na kostku ledu a napíšeme pro ni pohybovou rovnici.
Síly působící na kostku ledu:
\(\vec{F}_\mathrm{G}\)…síla tíhová
\(\vec{N}\)…síla, kterou tlačí podložka na kostku ledu
\(\vec{F}_\mathrm{x}\)…časově proměnlivá síla působící na kostku ledu
Pohybová rovnice pro kostku ledu:
\[\vec{F}_\mathrm{x}+\vec{F}_\mathrm{g}+\vec{N}\,=\, m\vec{a}\tag{1}\]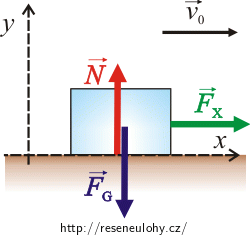
Pohybovou rovnici přepíšeme skalárně. Osu x zvolíme ve směru pohybu kostky ledu. Osa y je kolmá na osu x:
\[x:\qquad F_\mathrm{x} \,=\, ma\] \[(q-t) \,=\, ma\] \[\frac{p(q-t)}{m} \,=\, a\tag{2}\] \[y:\qquad N - F_\mathrm{G}\,=\,0\tag{3}\](zrychlení kostky ledu ve směru osy y je nulové).
Integrací zrychlení ve vztahu (2) dostaneme závislost rychlosti na čase:
\[v(t)=\int{a(t)}\,dt\] \[v(t)\,= \int{\frac{p(q-t)}{m}}\,\mathrm{d}t\,= \int{\frac{pq}{m}}\,\mathrm{d}t\,-\int{\frac{pt}{m}}\,\mathrm{d}t\,= \frac{pgt}{m}\,-\,\frac{pt^2}{2m}+C.\tag{4}\]V čase t = 0 s je rychlost rovna v0. Platí tedy:
\[v_0\,=\,\frac{pg}{m}\cdot0\,-\,\frac{p\cdot0}{2m}\,+\,C.\]Odtud:
\[v_0\,=\,C.\]Dosazením do vztahu (4) dostáváme:
\[v(t)\,=\,\frac{pgt}{m}\,-\,\frac{pt^2}{2m}\,+\,v_0.\tag{5}\]Integrací rychlosti ve vztahu (5) dostaneme závislost dráhy na čase:
\[x(t)\,=\,\int{v(t)}\,\mathrm{d}t\] \[x(t)\,=\, \int{(\frac{pqt}{m}\,-\,\frac{pt^2}{2m}\,+\,v_0})\,\mathrm{d}t\,=\, \frac{pqt^2}{2m}\,-\,\frac{pt^3}{6m}\,+\,v_0t\,+\,K.\tag{6}\]V čase t = 0 s je uražená dráha 0 m. Platí tedy:
\[0\,=\,\frac{pq\cdot0}{2m}\,-\,\frac{p\cdot0}{6m}\,+\,v_0{\cdot}0\,+\,K.\]Odtud:
\[0\,=\,K.\]Dosazením do vztahu (6) dostaneme:
\[x(t)\,=\,\frac{pqt^2}{2m}\,-\,\frac{pt^3}{6m}\,+\,v_0t.\tag{7}\]V okamžiku zastavení je rychlost rovna nule.
Pro čas zastavení tz tedy podle vztahu (5) platí:
\[0=\frac{pqt_\mathrm{z}}{m}-\frac{pt_\mathrm{z}^2}{2m}+v_0.\]Dostáváme kvadratickou rovnici s neznámou tz:
\[0=-\frac{pt_\mathrm{z}^2}{2m}+\frac{pqt_\mathrm{z}}{m}+v_0.\tag{8}\]Vyřešíme rovnici (8), nejprve spočteme diskriminant:
\[D=\frac{p^2q^2}{m^2}-4\left(-\frac{v_0p}{2m}\right)= \frac{p}{m}\left(\frac{pq^2}{m}+2v_0\right).\]Dále spočteme neznámou tz, dostáváme 2 matematická řešení:
\[t_\mathrm{z_1}=\frac{-\frac{pq}{m}+\sqrt{D}}{-\frac{p}{m}}\] \[t_\mathrm{z_2}=\frac{-\frac{pq}{m}-\sqrt{D}}{-\frac{p}{m}}.\]Odtud po dosazení D dostáváme:
\[t_\mathrm{z_1}=\frac{-\frac{pq}{m}+\sqrt{\frac{p}{m} \left(\frac{pq^2}{m}+2v_0\right)}}{-\frac{p}{m}}=q-\frac{m}{p}\sqrt{\frac{p}{m} \left(\frac{pq^2}{m}+2v_0\right)}\] \[t_\mathrm{z_1}=q-\sqrt{q^2+\frac{2mv_0}{p}}\tag{9}\] \[t_\mathrm{z_2}=\frac{-\frac{pq}{m}-\sqrt{\frac{p}{m}\left(\frac{pq^2}{m}+2v_0\right)}}{-\frac{p}{m}}= q+\frac{m}{p}\sqrt{\frac{p}{m}\left(\frac{pq^2}{m}+2v_0\right)}\] \[t_\mathrm{z_2}=q+\sqrt{q^2+\frac{2mv_0}{p}}.\tag{10}\]Do vztahu (9) a (10) dosadíme číselně:
\[t_\mathrm{z_1}=1-\sqrt{1^2+\frac{2{\cdot}10\cdot0{,}2}{100}}=1-\sqrt{\frac{104}{100}}= 1-1{,}02=-0{,}02\,\textrm{s}\] \[t_\mathrm{z_2}=1+\sqrt{1^2+\frac{2{\cdot}10\cdot0{,}2}{100}}=1+\sqrt{\frac{104}{100}}= 1+1{,}02=2{,}02\,\textrm{s}.\tag{11}\]Fyzikální význam má jen kladný čas \(t_\mathrm{z_2}\) z výsledku (11).
Známe čas zastavení tz2 = tz ve výsledku (11) a také závislost uražené dráhy na čase ze vztahu (7):
\[x(t)=\frac{pqt^2}{2m}\,-\,\frac{pt^3}{6m}+v_0t\tag{7}\] \[t_\mathrm{z}=2{,}02\,\mathrm{s}.\tag{11}\]Dráhu zastavení spočítáme dosazením času zastavení (11) do vztahu (7):
\[x(t_\mathrm{z})=\frac{pqt_\mathrm{z}^2}{2m}\,-\,\frac{pt_\mathrm{z}^3}{6m}+v_0t_\mathrm{z}\]Dosadíme číselně:
\[x(t_\mathrm{z})=\left(\frac{100{\cdot}1\cdot(2{,}02)^2}{2{\cdot}10}\,-\, \frac{100\cdot\left(2{,}02\right)^3}{6{\cdot}10}\,+\,0{,}2{\cdot}2{,}02\right)\,\textrm{m}\] \[x(t_\mathrm{z})=\left(20{,}40\,-\,13{,}74\,+\,0{,}40\right)\,\textrm{m}=7{,}06\,\textrm{m}.\tag{12}\]CELKOVÁ ODPOVĚĎ
Kostka ledu se zastavila za 2,02 s ve vzdálenosti 7,06 m od počátku zvolené soustavy souřadnic.



