Pohyb daný graficky II
Úloha číslo: 134
Grafy na obrázcích:
a) Považujte za průběhy souřadnice x(t) přímočarého pohybu a nakreslete k nim příslušné grafy vx(t).
b) Považujte za průběhy souřadnice rychlosti vx(t) přímočarého pohybu a nakreslete k nim příslušné průběhy x(t).
Znázorňují grafy reálné pohyby? Zkuste je znázornit pohybem prstu.
Nápověda 1 pro a): Rozdělení na intervaly
Považujte grafy na obrázcích za průběhy funkcí x(t), kde x(t) je závislost souřadnice x na čase t.
Rozdělte si průběhy funkcí na jednotlivé časové intervaly.
Jak se na nich souřadnice s časem mění? Zapište to rovnicemi.
Nápověda 2 pro a): Popisy pohybů
Z rovnic závislostí x(t) v předchozí nápovědě odvoďte rovnice závislostí vx(t) pro jednotlivé časové intervaly a nakreslete průběhy funkcí vx(t) v těchto intervalech.
Jaký pohyb funkce představují?
Nápověda 3 pro a): Reálnost pohybu
Zkuste si znázornit uvedené pohyby pohybem prstu. Jsou možné skokové přechody rychlosti podle grafu?
Nápověda 4 pro b): Rozdělení na intervaly
Považujte grafy na obrázcích za průběhy funkcí vx(t), kde vx(t) je závislost souřadnice rychlosti v na čase t.
Postupujte podobně jako u Nápovědy 1 a 2 pro a):
Rozdělte si průběhy funkcí na jednotlivé intervaly. O jaké funkce se na jednotlivých intervalech jedná? Napište jejich rovnice.
Nápověda 5 pro b): Popisy pohybů
Z rovnic závislostí vx(t) v předchozí nápovědě odvoďte rovnice závislostí x(t) pro jednotlivé intervaly a nakreslete průběhy funkcí x(t) na těchto intervalech.
Jaký pohyb funkce představují?
Nápověda 6 pro b): Reálnost pohybu
Zkuste si znázornit uvedené pohyby pohybem prstu.
CELKOVÉ ŘEŠENÍ
bod a):
Považujme grafy na obrázcích za průběhy funkcí x(t), kde x(t) je závislost souřadnice x na čase t.
Rozdělíme si průběhy funkcí na jednotlivé časové intervaly.
Zjistíme, o jaké funkce se na jednotlivých intervalech jedná, a napíšeme jejich rovnice.
Poznámka: Rovnice by měly být zapsány ve tvaru např.
x = 1 m − 2 m·s−1.t,
Pro zjednodušení zápisu jednotky ve vztazích nepíšeme.
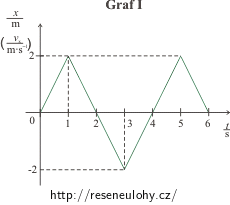
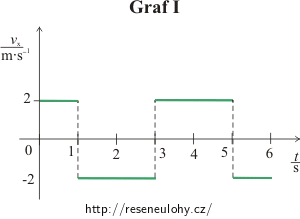
U grafu I. jsou to následující časové intervaly:
<0; 1 s> funkcí je přímka x(t) = 2t (souřadnice rovnoměrně narůstá),
(1 s; 3 s> funkcí je přímka x(t) = −2t + 4 (souřadnice rovnoměrně klesá),
(3 s; 5 s> funkcí je přímka x(t) = 2t − 8 (souřadnice rovnoměrně roste),
(5 s; 6 s> funkcí je přímka x(t) = −2t + 12 (souřadnice rovnoměrně klesá).
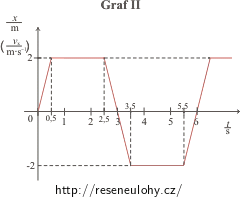
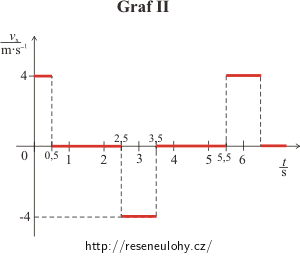
U grafu II. jsou to následující časové intervaly:
<0; 0,5 s> funkcí je přímka x(t) = 4t (souřadnice rovnoměrně narůstá),
(0,5 s; 2,5 s> funkcí je přímka x(t) = 2 (souřadnice se nemění),
(2,5 s; 3,5 s> funkcí je přímka x(t) = −4t + 12 (souřadnice rovnoměrně klesá),
(3,5 s; 5,5 s> funkcí je přímka x(t) = −2 (souřadnice se nemění),
(5,5 s; 6,5 s> funkcí je přímka x(t) = 4t − 24 (souřadnice rovnoměrně roste),
(6,5 s; 8,5 s> funkcí je přímka x(t) = 2 (souřadnice se nemění).
Z rovnic závislostí x(t) odvodíme rovnice závislostí vx(t) pro jednotlivé intervaly a nakreslíme průběhy funkcí vx(t) na těchto intervalech.
Závislost souřadnice rychlosti na čase vx(t) získáme derivováním závislosti souřadnice na čase x(t).
Graf I.:
Na intervalu <0; 1 s>:
\[v_\mathrm{x}(t) = \frac{\mathrm{d}x(t)}{\mathrm{d}t} = \frac{d(2t)}{\mathrm{d}t} = 2.\]
Objekt se pohybuje rovnoměrně s konstantní rychlostí o velikosti 2 m·s−1 ve směru osy x.
Na intervalu (1 s; 3 s>:
\[v_\mathrm{x}(t)\,=\,\frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(-2t + 4)}{\mathrm{d}t} \,= -2.\]
Objekt se pohybuje rovnoměrně s konstantní rychlostí o velikosti 2 m·s−1 proti směru osy x.
Na intervalu (3 s; 5 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(2t - 8)}{\mathrm{d}t} \,=\, 2.\]
Objekt se pohybuje rovnoměrně s konstantní rychlostí o velikosti 2 m·s−1 ve směru osy x.
Na intervalu (5 s; 6 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(-2t + 12)}{\mathrm{d}t} \,=\, -2.\]
Objekt se pohybuje rovnoměrně s konstantní rychlostí o velikosti 2 m·s−1 proti směru osy x.
Graf II.:
Na intervalu <0; 0,5 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(4t)}{\mathrm{d}t} \,=\, 4.\]
Objekt se pohybuje rovnoměrně s konstantní rychlostí o velikosti 4 m·s−1 ve směru osy x.
Na intervalu (0,5 s; 2,5 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(2)}{\mathrm{d}t} \,=\, 0.\]
Objekt se nepohybuje, je v klidu (vx = 0 m·s−1).
Na intervalu (2,5 s; 3,5 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(-4t + 12)}{\mathrm{d}t} \,=\, -4.\]
Objekt se pohybuje rovnoměrně s konstantní rychlostí o velikosti 4 m·s−1 proti směru osy x.
Na intervalu (3,5 s; 5,5 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(-2)}{\mathrm{d}t} \,=\, 0.\]
Objekt se nepohybuje, je v klidu (vx = 0 m·s−1).
Na intervalu (5,5 s; 6,5 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{d(4t - 24)}{\mathrm{d}t} \,=\, 4.\]
Objekt se pohybuje rovnoměrně s konstantní rychlostí o velikosti 4 m·s−1 ve směru osy x.
Na intervalu (6,5 s; 8,5 s>:
\[v_\mathrm{x}(t) \,=\, \frac{\mathrm{d}x(t)}{\mathrm{d}t} \,=\, \frac{\mathrm{d}(2)}{\mathrm{d}t} \,=\, 0.\]
Objekt se nepohybuje, je v klidu (vx = 0 m·s−1).
Nejde o reálné pohyby.
Při reálném pohybu se nemůže rychlost skokem změnit. Při znázornění pohybem prstu musí prst postupně zpomalit na nulovou rychlost a pak se rozjet na druhou stranu. V grafu x(t) by pro reálný pohyb nebyly ostré špičky.
bod b):
Postupujeme obdobně jako u a).
Poznámka: Opět pro zjednodušení zápisu jednotky ve vztazích nepíšeme.
Grafy na obrázcích považujeme za průběhy funkcí vx(t), kde vx(t) je závislost souřadnice rychlosti v na čase t.
Průběhy funkcí si rozdělíme na jednotlivé intervaly. Napíšeme, o jaké funkce se na jednotlivých intervalech jedná, a zapíšeme je rovnicí.
U grafu I. jsou to následující intervaly:
<0; 1 s> funkcí je přímka vx(t) = 2t,
(1 s; 3 s> funkcí je přímka vx(t) = −2t + 4,
(3 s; 5 s> funkcí je přímka vx(t) = 2t − 8,
(5 s; 6 s> funkcí je přímka vx(t) = −2t + 12.
U grafu II. jsou to následující intervaly:
<0; 0,5 s> funkcí je přímka vx(t) = 4t,
(0,5 s; 2,5 s> funkcí je přímka vx(t) = 2,
(2,5 s; 3,5 s> funkcí je přímka vx(t) = −4t + 12,
(3,5 s; 5,5 s> funkcí je přímka vx(t) = −2,
(5,5 s; 6,5 s> funkcí je přímka vx(t) = 4t − 24,
(6,5 s; 8,5 s> funkcí je přímka vx(t) = 2.
Z rovnic závislostí vx(t) v předchozí nápovědě odvodíme rovnice závislostí x(t) pro jednotlivé intervaly a nakreslíme průběhy funkcí x(t) na těchto intervalech.
Závislost souřadnice x(t) na čase získáme integrováním závislosti souřadnice rychlosti vx(t) na čase.
Poznámka: Pro zjednodušení zápisu jednotky ve vztazích opět nepíšeme.
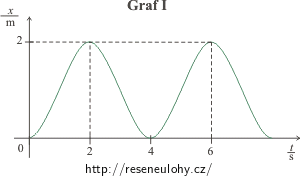
Graf I.:
Na intervalu <0; 1 s>:
\[x(t)\,=\,\int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{2t}\mathrm{d}t,\]
\[x(t)\,=\, t^{2}+A.\]
Konstantu A zjistíme z počátečních podmínek:
V čase t = 0 s je x(0) = 0 m, po dosazení A = 0.
\(x(t) \,=\, t^{2}\)
Objekt se pohybuje rovnoměrně zrychleně přímočaře ve směru osy x.
Na intervalu (1 s; 3 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{(-2t+4)}\mathrm{d}t,\]
\[x(t) \,=\, -t^{2}+4t+B.\]
Konstantu B zjistíme z počátečních podmínek:
Souřadnici v čase t = 1 s zjistíme dosazením do předchozí závislosti \(x(t)\,=\,t^{2}\), tedy x(1) = 1 m.
Po dosazení: 1 = −12 + 4·1 + B, a tedy B = −2.
\(x(t) \,=\, -t^{2}+4t-2\)
Objekt se pohybuje rovnoměrně zpomaleně přímočaře ve směru osy x. V čase t = 2 s je rychlost nulová, směr pohybu se obrací a objekt se pohybuje rovnoměrně zrychleně přímočaře proti směru osy x.
Na intervalu (3 s; 5 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{(2t-8)}\mathrm{d}t,\]
\[x(t) \,=\, t^{2}-8t+C.\]
Konstantu C zjistíme z počátečních podmínek:
Souřadnici v čase t = 3 s zjistíme dosazením do předchozí závislosti \(x(t)\,=\,-t^{2}+4t-2\), tedy x(3) = 1 m.
Po dosazení: 1 = 32−8·3 + C, a tedy C = 16.
\(x(t)\,=\,t^{2}-8t+16\)
Objekt se začne pohybovat rovnoměrně zpomaleně přímočaře proti směru osy x. V čase t = 4 s je rychlost nulová, směr pohybu se obrací a objekt se pohybuje rovnoměrně zrychleně přímočaře ve směru osy x.
Na intervalu (5 s; 6 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{(-2t+12)}\mathrm{d}t,\]
\[x(t)\,=\,-t^{2}+12t+D.\]
Konstantu D zjistíme z počátečních podmínek:
Souřadnici v čase t = 5 s zjistíme dosazením do předchozí závislosti \(x\,=\,t^{2}-8t+16\), tedy x(5) = 1 m.
Po dosazení: 1 = −52+12·5 + D, a tedy D = −34.
\(x(t) \,=\, -t^{2}+12t-34\)
Objekt se pohybuje rovnoměrně zpomaleně přímočaře ve směru osy x.
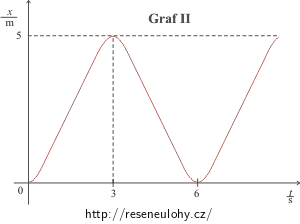
Graf II.:
Na intervalu <0; 0,5 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{4t}\mathrm{d}t,\]
\[x(t) \,=\, 2t^{2}+E.\]
Konstantu E zjistíme z počátečních podmínek:
V čase t = 0 s je x(0) = 0 m, po dosazení E = 0.
\(x(t) \,=\, 2t^{2}\)
Objekt se pohybuje rovnoměrně zrychleně přímočaře ve směru osy x.
Na intervalu (0,5 s; 2,5 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{2}\mathrm{d}t,\]
\[x(t) \,=\, 2t+F. \]
Konstantu F zjistíme z počátečních podmínek:
Souřadnici v čase t = 0,5 s zjistíme dosazením do předchozí závislosti \(x(t)\,=\,2t^{2}\), tedy x(0,5) = 0,5 m.
Po dosazení: 0,5 = 2·0,5+F, a tedy F = −0,5.
\(x(t) \,=\, 2t-0{,}5\)
Objekt se pohybuje rovnoměrně přímočaře s konstantní rychlostí o velikosti 2 m·s−1 ve směru osy x.
Na intervalu (2,5 s; 3,5 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{(-4t+12)}\mathrm{d}t,\]
\[x(t) \,=\, -2t^{2}+12t+G.\]
Konstantu G zjistíme z počátečních podmínek:
Souřadnici v čase t = 2,5 s zjistíme dosazením do předchozí závislosti \(x(t)\,=\,2t-0{,}5\), tedy x(2,5) = 4,5 m.
Po dosazení: 4,5 = −2·2,52 + 12·2,5 + G, a tedy G = −13.
\(x(t) \,=\, -2t^{2}+12t-13\)
Objekt se pohybuje rovnoměrně zpomaleně přímočaře ve směru osy x. V čase t = 3 s je rychlost nulová, směr pohybu se obrací a objekt se pohybuje rovnoměrně zrychleně proti směru osy x.
Na intervalu (3,5 s; 5,5 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{-2}\mathrm{d}t,\]
\[x(t) \,=\, -2t+H. \]
Konstantu H zjistíme z počátečních podmínek:
Souřadnici v čase t = 3,5 s zjistíme dosazením do předchozí závislosti \(x(t)\,=\,-2t^{2}+12t-13\), tedy x(3,5) = 4,5 m.
Po dosazení: 4,5 = −2·3,5 + H, a tedy H = 11,5.
\(x(t) \,=\, -2t+11{,}5 \)
Objekt se pohybuje rovnoměrně přímočaře s konstantní rychlostí o velikosti 2 m·s−1 proti směru osy x.
Na intervalu (5,5 s; 6,5 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{(4t-24)}\mathrm{d}t,\]
\[x(t) \,=\, 2t^{2}-24t+K.\]
Konstantu K zjistíme z počátečních podmínek:
Souřadnici v čase t = 5,5 s zjistíme dosazením do předchozí závislosti \(x(t)\,=\,-2t+11{,}5 \), tedy x(5,5) = 0,5 m.
Po dosazení: 0,5 = 2·5,52−24·5,5 + K, a tedy K = 72.
\(x(t) \,=\, 2t^{2}-24t+72\)
Objekt se pohybuje rovnoměrně zpomaleně přímočaře proti směru osy x. V čase t = 6 s je rychlost pohybu nulová směr pohybu se obrací a objekt se pohybuje rovnoměrně zrychleně ve směru osy x.
Na intervalu (6,5 s; 8,5 s>:
\[x(t) \,=\, \int{v_\mathrm{x}(t)}\mathrm{d}t\,=\,\int{2}\mathrm{d}t,\]
\[x(t) \,=\, 2t+L. \]
Konstantu L zjistíme z počátečních podmínek:
Souřadnici v čase t = 6,5 s zjistíme dosazením do předchozí závislosti \(x(t)\,=\,2t^{2}-24t+72\), tedy x(6,5) = 0,5 m.
Po dosazení: 0,5 = 2·6,5 + L, a tedy L = −12,5.
\(x(t) \,=\, 2t-12{,}5 \)
Objekt se pohybuje rovnoměrně přímočaře s konstantní rychlostí o velikosti 2 m·s−1 ve směru osy x.
Jedná se o reálný pohyb.
Graf I: Prst se pohybuje např. směrem doprava a po dobu 1 s rovnoměrně zrychluje, pak začne ve stejném směru po dobu 1 s rovnoměrně zpomalovat. V čase 2 s je jeho rychlost nulová a směr pohybu se obrací. Prst se pohybuje směrem doleva a po dobu 1 s rovnoměrně zrychluje, pak začne ve stejném směru po dobu 1 s rovnoměrně zpomalovat. V čase 4 s je ve stejném místě, kde pohyb začínal, jeho rychlost je nulová a pohyb se začíná opakovat.
Graf II: Prst se pohybuje např. směrem doprava a po dobu 0,5 s rovnoměrně zrychluje, pak se pohybuje rovnoměrně přímočaře po dobu 2 s. Poté začne jeho rychlost rovnoměrně klesat, a to po dobu 0,5 s až na nulu. Pak se směr pohybu obrátí, rychlost prstu po dobu 0,5 s rovnoměrně narůstá, pak je jeho pohyb po dobu 2 s opět rovnoměrně přímočarý a pak po dobu 0,5 s rychlost rovnoměrně klesá až na nulu. V čase t = 6 s je prst ve stejném místě, kde pohyb začínal, jeho rychlost je nulová a pohyb se začíná opakovat.
Odpověď