Chataři od Lančovské zátoky
Úloha číslo: 124
Obyvatelé Lančovské zátoky mají postavené chatky blízko řeky Dyje, která je v úseku zátoky široká L. Když se chtějí sousedé navštívit, použijí k dopravě loďku.
Chatař Nesnídal vlastní loďku, která jezdí na klidné vodě konstantní rychlostí o velikosti vl. Rozhodne se, že spolu se svým sousedem Nekvapilem navštíví chataře Nesvačila.
Určete, jak dlouho jim celá plavba potrvá, víte-li následující:
Nesnídal pojede nejprve pro Nekvapila, který bydlí na téže straně řeky proti proudu řeky ve vzdálenosti x od něj. Poté oba poplují k Nesvačilově chatce, která se nachází na druhém břehu přímo proti Nekvapilově chatě.
Předpokládejte, že rychlost proudu řeky je konstantní a má velikost vr.
Řešte pro hodnoty: L = 200 m, vl = 2 m·s-1, vr = 1 m·s-1, x = 500 m.
Zápis
L = 200 m šířka řeky vl = 2 m·s−1 rychlost loďky na stojaté vodě vr = 1 m·s−1 rychlost říčního proudu x = 500 m vzdálenost chatek sousedů Nesnídala a Nekvapila ve směru proti proudu řeky t = ? (s) doba celé plavby Nápověda 1: Čas t1 od Nesnídala k Nekvapilovi
Určete čas t1, za který dopluje Nesnídal k Nekvapilovi.
Znáte délku trasy. Jak velkou rychlostí v1 plul Nesnídal k Nekvapilovi?
Nakreslete si obrázek situace.
Nápověda 2: Čas t2 od Nekvapila k Nesvačilovi
Určete čas t2, za který Nesnídal s Nekvapilem doplují k Nesvačilovi.
Délku trasy opět znáte. Jakým způsobem poplují? Mohou si to namířit přímo k Nesvačilově chatě?
Jak velkou rychlostí v2 poplují? Nakreslete si obrázek.
Nápověda 3: Výsledná doba t plavby
Co platí pro výslednou dobu t celé plavby? Stačí vám k jejímu vyjádření předchozí výpočty?
CELKOVÉ ŘEŠENÍ:
Nejprve určíme čas t1, za který dopluje Nesnídal k Nekvapilovi, a poté čas t2, za který oba doplují k Nesvačilovi. Sečtením obou časů získáme výslednou dobu celé plavby:
\[t=t_1+t_2.\]
Čas t1 od Nesnídala k Nekvapilovi:
Obrázek 1:
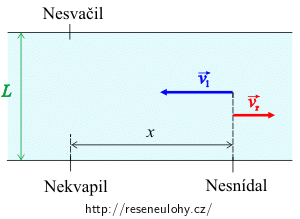
Velikost rychlosti v1 loďky vzhledem k břehu, pluje-li proti proudu, je daná rozdílem rychlosti loďky vzhledem ke klidné vodě vl a rychlosti proudu vr:
\[v_1=v_\mathrm{l}-v_\mathrm{r}.\]Touto rychlostí má loďka uplout vzdálenost x. Potrvá jí to čas t1:
\[t_1=\frac{x}{v_\mathrm{l}-v_\mathrm{r}}.\]Čas t2 od Nekvapila k Nesvačilovi:
Chtějí-li Nesnídal s Nekvapilem připlout přímo k Nesvačilově chatě, nemohou si to namířit přímo na ni (proud by je snesl), ale tak, jak je naznačeno na obrázku:
Obrázek 2:
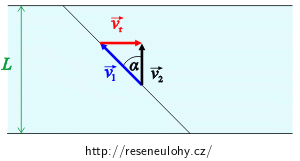
Výsledná rychlost:
\[v_2=\sqrt{v_\mathrm{l}^{2}-v_\mathrm{r}^{2}}.\]Čas t2:
\[t_2=\frac{L}{v_2}=\frac{L}{\sqrt{v_\mathrm{l}^{2}-v_\mathrm{r}^{2}}}.\]Určili jsme čas t1, za který doplul Nesnídal k Nekvapilovi, a poté čas t2, za který oba dopluli k Nesvačilovi.
Sečtením obou časů získáme výslednou dobu t celé plavby:
\[ t=t_1+t_2=\frac{x}{v_\mathrm{l}-v_\mathrm{r}}+\frac{L}{\sqrt{v_\mathrm{l}^{2}-v_\mathrm{r}^{2}}}.\]Číselně:
\[t=\left(\frac{500}{2-1}+\frac{200}{\sqrt{3}}\right)\,\mathrm{s}=615\,\mathrm{s}.\]Odpověď
Chataři Nesnídal a Nekvapil doplují k chataři Nesvačilovi za dobu t:
\[ t=\frac{x}{v_\mathrm{l}-v_\mathrm{r}}+\frac{L}{\sqrt{v_\mathrm{l}^{2}-v_\mathrm{r}^{2}}}.\]Číselně:
\[t=615\,\mathrm{s}.\]



