Kapilára v rozjíždějícím se výtahu
Úloha číslo: 2032
Ve svislé skleněné kapiláře vystoupila voda do výšky h = 125 mm. Jak se změní výška sloupce vody v kapiláře, bude-li umístěna v těžní kleci důlního výtahu, která se rozjíždí směrem dolů se zrychlením a = 6 m·s−2?
Rozbor
Nejdříve se zamyslíme nad situací, kdy výtah ještě stojí a kapilára s vodou je v klidu. Výslednice sil, které na vodu působí, je nulová. Tíhová síla působící na vodu v kapiláře je rovna výslednici povrchových sil, které na vodu působí u zakřiveného povrchu. (Kdyby se výtah pohyboval rovnoměrně přímočaře, byla by výslednice sil také nulová.)
Situaci, kdy výtah začne klesat s daným zrychlením, popíšeme nejdříve z pohledu pozorovatele, který zůstal stát mimo výtah (tedy z pohledu inerciální vztažné soustavy). Z jeho pohledu se kapilára s vodou pohybuje rovnoměrně zrychleně dolů. Výslednice sil působících na vodu směřuje dolů. Na vodu působí opět tíhová síla a výslednice povrchových sil.
Povrchová síla závisí na poloměru kapiláry a povrchovém napětí vody - ty zůstávají stejné, takže zůstane stejná i velikost povrchové síly. Voda v kapiláře bude muset vystoupat výše, aby vzrostla tíhová síla působící na vodu.
Na situaci se také můžeme podívat z pohledu pozorovatele, který je ve výtahu (z pohledu neinerciální vztažné soustavy). Vzhledem k němu jsou kapilára i voda v ní v klidu. Výslednice sil působících na vodu je tedy z jeho pohledu nulová. Kromě tíhové síly a výslednice povrchových sil působí na vodu ještě setrvačná síla mířící vzhůru.
Nápověda část 1 - kapilára v klidu nebo rovnoměrném přímočarém pohybu
Rozmyslete si, jaké síly působí na vodu v kapiláře a jaká je jejich výslednice, jestliže výtah stojí nebo se pohybuje rovnoměrným přímočarým pohybem. Napište pak vztahy pro velikosti těchto sil a vyjádřete z nich výšku, do které vystoupí hladina vody v kapiláře v této situaci.
Řešení část 1 - kapilára v klidu nebo rovnoměrném přímočarém pohybu
Na vodu působí tíhová síla Fg a výslednice povrchových sil Fk. Kapilára s vodou je v klidu, výslednice sil působících na vodu musí být nulová.
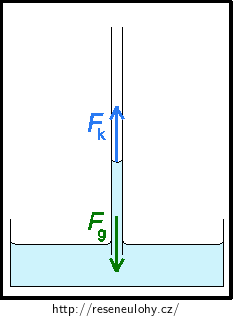
Platí tedy
\[F_\mathrm{g} = F_\mathrm{k}.\tag{1}\]Tíhovou sílu můžeme vyjádřit jako součin hmotnosti m a tíhového zrychlení g
\[F_\mathrm{g} = mg.\tag{2}\]Síla Fk je daná součinem kapilárního tlaku pk a obsahu plochy vnitřního průřezu kapiláry S
\[F_\mathrm{k} = p_\mathrm{k}S.\tag{3}\]Dosadíme-li do vztahu (1) rovnice (2) a (3), získáme rovnost
\[mg = p_\mathrm{k}S.\tag{4}\]Chceme zjistit výšku hladiny vody v kapiláře h1. Hmotnost vody m můžeme vyjádřit jako součin hustoty ρ a objemu V vody. Objem lze ještě vyjádřit jako součin výšky sloupce vody h1 s plochou S
\[m = ρ·V = ρ·h_\mathrm{1}S.\tag{5}\]Dosazením (5) do (4) pak získáme rovnost
\[ρh_\mathrm{1}Sg = p_\mathrm{k}S.\tag{6}\]Rovnici (6) upravíme a vyjádříme výšku hladiny vody h1 v kapiláře, která je v klidu
\[h_\mathrm{1} = \frac{p_\mathrm{k}}{ρg}.\tag{7}\]Kapilární tlak vypočítáme jako
\[p_\mathrm{k} = \frac{2σ}{r},\tag{8}\]kde σ je povrchové napětí vody a r poloměr kapiláry.
Do vztahu (7) dosadíme za kapilární tlak ze vztahu (8)
\[h_\mathrm{1} = \frac{2σ}{rρg}.\tag{9}\]Nápověda část 2 - kapilára v rozjíždějícím se výtahu z pohledu inerciálního pozorovatele
Jaké síly působí na vodu v kapiláře, která je umístěná ve výtahu rozjíždějícím se směrem dolů se zrychlením a? Kam směřuje jejich výslednice a jaká bude velikost sil ve srovnání s předchozí situací, kdy byl výtah v klidu? Jak se změní výška hladiny vody v kapiláře?
Situaci řešte nejprve z pohledu pozorovatele, který stojí v klidu mimo výtah (inerciální pozorovatel).
Řešení část 2 - kapilára v rozjíždějícím se výtahu z pohledu inerciálního pozorovatele
Pozorovatel stojí v klidu mimo výtah - inerciální pozorovatel
Z pohledu inerciálního pozorovatele působí na vodu v kapiláře směrem dolů tíhová síla Fg a v opačném směru výslednice povrchových sil Fk.
Výtah i kapilára s vodou se pohybují se zrychlením směrem dolů. Na vodu tedy působí nenulová výsledná síla F směřující dolů:
\[F = ma,\tag{10}\]kde a je zrychlení, se kterým se pohybují výtah i voda v kapiláře.
Výslednice povrchových sil, která závisí na povrchovém napětí vody a poloměru kapiláry, bude mít stejnou velikost jako v situaci, kdy je výtah v klidu. Musí tedy vzrůst tíhová síla působící na vodu v kapiláře, voda v ní tedy vystoupá výš.
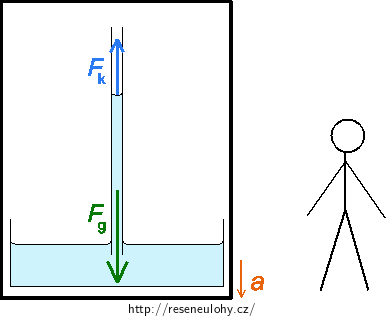
Pro velikosti sil platí
\[F_\mathrm{g}−F_\mathrm{k} = F.\tag{11}\]Do rovnice (11) dosadíme ze vztahů (2), (3) a (10) a získáme tak rovnici
\[mg−p_\mathrm{k}S = ma\] \[m(g−a) = p_\mathrm{k}S\tag{12}\]Výšku hladiny vody h2 v kapiláře zjistíme po několika úpravách vztahu (12). Nejdříve vyjádříme hmotnost vody m jako součin hustoty a objemu vody v kapiláře
\[m = ρ·V = ρ·h_\mathrm{2}S.\]a tento vztah pro hmotnost dosadíme do vztahu (12). Získáme tak rovnici
\[ρh_\mathrm{2}S(g−a) = p_\mathrm{k}S.\tag{13}\]Vztah (13) upravíme, dosadíme za kapilární tlak ze vztahu (8) a následně vyjádříme výšku hladiny h2 kapaliny v rozjíždějícím se výtahu
\[ρh_\mathrm{2}(g−a) = \frac{2σ}{r}\] \[h_\mathrm{2} = \frac{2σ}{rρ(g−a)}.\tag{14}\]Změnu výšky sloupce vody Δh vypočítáme jako rozdíl výšky hladiny vody v rozjíždějícím se výtahu h2 a výšky hladiny vody v klidu h1 (rozdíl vztahů (14) a (9))
\[Δh = h_\mathrm{2}−h_\mathrm{1} = \frac{2σ}{rρ(g−a)}−\frac{2σ}{rρg}.\]Tuto rovnici upravíme
\[Δh = \frac{2σa}{rρg(g−a)} \tag{15}\]a následně rovnici (15) zjednodušíme s využitím vztahu (9)
\[Δh = h_\mathrm{1}\frac{a}{g−a}.\tag{16}\]Nápověda část 3 - kapilára v rozjíždějícím se výtahu z pohledu neinerciálního pozorovatele
Situaci můžeme také řešit z pohledu pozorovatele, který stojí ve výtahu (neinerciální pozorovatel).
Rozmyslete si, jak se vzhledem k tomuto pozorovateli pohybuje kapilára s vodou, jaké síly působí na vodu v kapiláře z pohledu pozorovatele a jaká je jejich výslednice.
Řešení část 3 - kapilára v rozjíždějícím se výtahu z pohledu neinerciálního pozorovatele
Pozorovatel stojící ve výtahu - neinerciální pozorovatel
Vůči pozorovateli ve výtahu je voda v kapiláře v klidu, výslednice sil působících na vodu tedy musí být nulová. Na vodu působí stejně jako v části 2 tíhová síla Fg a výslednice povrchových sil Fk a kromě nich ještě setrvačná síla Fs, která existuje jen v neinerciální vztažné soustavě.
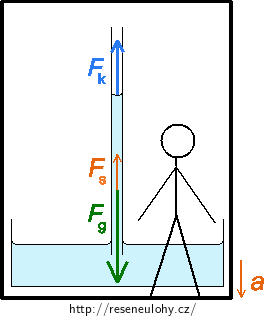
Pro výslednici sil platí
\[\vec{F_\mathrm{g}}+\vec{F_\mathrm{k}}+\vec{F_\mathrm{s}} = 0.\]Tíhová síla míří směrem dolů, výslednice povrchových sil Fk i setrvačná síla Fs míří vzhůru. Pro velikosti těchto sil platí
\[F_\mathrm{g}−F_\mathrm{k}−ma = 0.\]Za síly Fg i Fk dosadíme ze vztahů (2) a (3)
\[mg−p_\mathrm{k}S−ma = 0.\]Tento vztah upravíme na tvar
\[m(g−a) = p_\mathrm{k}S.\tag{12}\]Získali jsme stejný vztah (12) jako v předchozí části, kdy jsme situaci řešili z pohledu inerciálního pozorovatele. Úlohu bychom dále řešili stejným způsobem a pro rozdíl výšek hladin bychom také získali vztah (16)
\[Δh = h_\mathrm{1}\frac{a}{g−a}.\tag{16}\]Ať budeme kapiláru pozorovat zevnitř pohybujícího se výtahu, či se budeme na klesající výtah dívat zvenku, uvidíme, že voda v kapiláře pohybující se zrychleně směrem dolů vystoupá výš o stejný kus Δh oproti kapiláře, která je v klidu.
Číselné dosazení
Rozdíl výšek hladin vody Δh mezi kapilárou v klidu a kapilárou v rozjíždějícím se výtahu určíme ze vztahu (16)
\[Δh = h_\mathrm{1}\frac{a}{g−a}.\tag{16}\]Dosadíme zadané hodnoty a vypočítáme
\[Δh = 1{,}25·10^{−1}·\frac{6}{10−6} \mathrm{m}\] \[Δh \dot{=}\, 187{,}5·10^{−3} \mathrm{m} \dot{=}\, 187{,}5 \mathrm{mm}.\]Odpověď
Hladina vody v kapiláře umístěné ve výtahu, který se rozjíždí směrem dolů se zrychlením 6 m·s−1, bude o 187,5 mm výše než v kapiláře, která je v klidu.




