Dokonale pružná srážka
Úloha číslo: 32
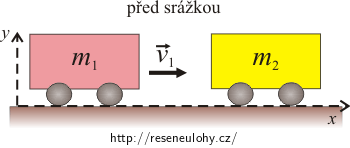
Na vzduchové dráze se srazí vozík dokonale pružně s druhým vozíkem, který byl do srážky v klidu. Po srážce se oba vozíky pohybují stejně velkými rychlostmi opačným směrem. Určete poměr hmotností obou vozíků.
Předpoklady
Předpokládejme, že jde o pohyb po přímce:
rychlosti před srážkou: \[\vec{v_{1}},\ \vec{v_{2}}\,=\, 0\ \mathrm{m s^{-1}} \]
rychlosti po srážce: \[ v_{1}^{'}\, =\, v_{2}^{'},\ \vec{v_{1}^{'}}\, = \, -\vec{v_{2}^{'}}\]
Nápověda 1 – zákony zachování
Jaké dva zákony zachování můžete využít při dokonale pružné srážce?
Nápověda 2 – ZZME a ZZH
Rozepište oba zákony pro naši konkrétní situaci.
Nápověda 3 – poměr hmotností
Z rovnic (1), (2) vyjádřete hledaný poměr \[\frac{m_{1}}{m_{2}}.\]
Odpověď
Poměr hmotností vozíků je \[ \frac {m_2} {m_1} \,=\, 3.\]
Celkové řešení
Předpokládejme, že jde o pohyb po přímce.
Rychlosti před srážkou: \[\vec{v_{1}},\ \vec{v_{2}}\,=\, 0\ \mathrm{m s^{-1}} \]
Rychlosti po srážce: \[ v_{1}^{'}\, =\, v_{2}^{'},\ \vec{v_{1}^{'}}\, = \, -\vec{v_{2}^{'}}\]
Pro dokonale pružnou srážku platí:
Zákon zachování hybnosti (ZZH):
Součet hybností těles v izolované soustavě je konstantní neboli celková hybnost izolované soustavy se zachovává.
Zákon zachování mechanické energie (ZZME):
Celková mechanická energie izolované soustavy se zachovává neboli součet potenciální a kinetické energie je konstantní.
 \[\mathrm{ZZH}:\qquad \vec{p_1} \,+\, \vec{p_2}\ \,=\,\ \vec{p_1^{'}} \,+\, \vec{p_2^{'}} \,,\]
\[\mathrm{ZZH}:\qquad \vec{p_1} \,+\, \vec{p_2}\ \,=\,\ \vec{p_1^{'}} \,+\, \vec{p_2^{'}} \,,\]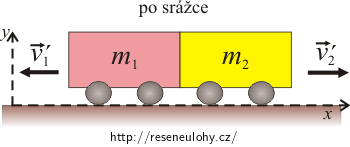
kde\(\hspace{20px} \vec{p_{1}}\) – hybnost 1. vozíku před srážkou,
\(\vec{p_{2}}\) – hybnost 2. vozíku před srážkou,
\(\vec{p_{1}^{'}}\) – hybnost 1. vozíku po srážce,
\(\vec{p_{2}^{'}}\) – hybnost 2. vozíku po srážce.
Dosadíme za hybnost:
\[m_{1}\vec{v_{1}}\,+\, 0\,=\,m_{1}\vec{v_{1}^{'}}\,+\,m_{2}\vec{v_{1}^{'}}\,.\]Zvolíme souřadný systém podle obrázku a přepíšeme skalárně:
\[m_{1}v_{1}\,=\,\,-m_{1}v_{1}^{'}\,+\,m_{2}v_{1}^{'}\tag{1}\] \[\mathrm{ZZME}: \qquad E_\mathrm{k1}+E_\mathrm{k2}=E_\mathrm{k1}^{'}+E_\mathrm{k2}^{'}\,,\]kde \( \hspace{15px} E_\mathrm{k1}\) – kinetická energie 1. vozíku před srážkou,
\(E_\mathrm{k2}\) – kinetická energie 2. vozíku před srážkou,
\(E_\mathrm{k1}^{'}\) – kinetická energie 1. vozíku po srážce,
\(E_\mathrm{k2}^{'}\) – kinetická energie 2. vozíku po srážce.
Dosadíme za kinetickou energii:
\[\ \frac{1}{2}m_{1}v_{1}^{2}\,+\,0\,=\,\frac{1}{2}m_{1}v_{1}^{'2}\,+\,\frac{1}{2}m_{2}v_{1}^{'2}\,.\tag{2}\]Rovnici (1) na pravé straně upravíme vytknutím \( v_{1}^{'}\)a pak ji umocníme. Rovnici (2) vynásobíme dvěma:
\[\mathrm{ZZH}:\hspace{10px} m_{1}v_{1}\,=\,-m_{1}v_{1}^{'}\,+\,m_{2}v_{1}^{'}\,=\,v_{1}^{'}(m_{2}-m_{1}) \hspace{25px}\,/^2\] \[\mathrm{ZZME}:\hspace{10px} \frac{1}{2}m_{1}v_{1}^{2}\,=\,\frac{1}{2}m_{1}v_{1}^{'2}\,+\,\frac{1}{2}m_{2}v_{1}^{'2} \hspace{25px}\,/\cdot 2.\]Dostali jsme tvar:
\[\ m_{1}^{2}v_{1}^{2}\,=\,v_{1}^{'2}(m_{2}-m_{1})^{2}\] \[ m_{1}v_{1}^{2}\,=\,v_{1}^{'2}(m_{1}\,+\,m_{2}).\]Vyjádříme si z obou rovnic \(v_{1}^{2}\) a dáme do rovnosti:
\[\frac{v_{1}^{'2}}{m_{1}^{2}}(m_{2}-m_{1})^{2}\,=\,\frac{v_{1}^{'2}}{m_{1}}(m_{1}\,+\,m_{2}).\]Protože složka \(\frac{v_{1}^{'2}}{m_{1}^{2}}\) je nenulová, můžeme s ní celou rovnici vydělit. Dostaneme:
\[(m_{2}-m_{1})^{2}\,=\,m_{1}(m_{1}\,+\,m_{2}).\]Zbývá nám rovnici upravit:
\[m_{2}^{2}-2m_{1}m_{2}\,+\,m_{1}^{2}\,=\,m_{1}^{2}\,+\,m_{1}m_{2}\] \[m_{2}^{2}-3m_{2}m_{1}\,=\,0\] \[m_{2}(m_{2}-3m_{1})\,=\,0.\]Protože hmotnost druhého vozíku není nula, musí platit:
\[m_{2}\,=\,3m_{1}\,.\]Pro poměr hmotností vozíků pak platí:
\[\frac{m_{2}}{m_{1}}\,=\,3\,.\]Odpověď: Poměr hmotností vozíků je \( \frac{m_{2}}{m_{1}}\,=\,3\,.\)




