Hozený kotouč
Úloha číslo: 535
Homogenní kruhový kotouč má poloměr R, hmotnost m a moment setrvačnosti \(J=\frac{1}{2}mR^2\). Neroztočený kotouč je s počáteční rychlostí v0 hozen ve svislé poloze na drsnou podložku tak, aby se začal kutálet. Koeficient smykového tření je f. Určete
a) okamžik, kdy se kotouč začne pohybovat čistým valením bez smýkání,
b) rychlost těžiště kotouče v tomto okamžiku,
c) vzdálenost, kterou kotouč urazí do tohoto okamžiku,
d) práci sil tření.
Zápis
R poloměr kotouče m hmotnost kotouče J = mR2/2 moment setrvačnosti kotouče v0 počáteční rychlost těžiště kotouče v čase t0 f koeficient smykového tření t1 = ? okamžik, kdy se kotouč začne pohybovat čistým valením bez smýkání v1 = ? rychlost těžiště kotouče v čase t1 s1 = ? vzdálenost, kterou kotouč urazí do času t1 W = ? práce sil tření Rozbor:
Hozený kotouč se po dopadu na podložku začne díky působení třecí síly postupně roztáčet. Po jistou dobu se však bude ještě také smýkat. Úhlová rychlost kotouče bude tedy postupně narůstat, zatímco rychlost posuvného pohybu těžiště bude klesat. Smýkání ustane v okamžiku, kdy bude platit, že rychlost těžiště kotouče je rovna součinu úhlové rychlosti otáčení kotouče a jeho poloměru.
Budeme tedy potřebovat napsat, jak se s časem mění rychlost těžiště kotouče a úhlová rychlost jeho otáčení. K tomu bude třeba zjistit, jaké síly na kotouč působí a jak ovlivňují jeho pohyb. K řešení posledního úkolu pak využijeme zákon zachování energie.
Nápověda 1
Jaké síly na kotouč působí? Zakreslete je do obrázku.
Nápověda 2
Napište 2. impulsovou větu pro kotouč, vyjádřete jeho úhlové zrychlení a úhlovou rychlost.
Nápověda 3
Napište pohybovou rovnici pro těžiště kotouče a vyjádřete, jak se s časem mění jeho zrychlení.
Nápověda 4a
Zapište podmínku, která musí platit pro rychlost těžiště kotouče a jeho úhlovou rychlost v okamžiku, kdy nastane čisté valení bez smýkání. Odtud pak vyjádřete hledaný čas.
Nápověda 5b
Víte, jak se s časem mění rychlost těžiště kotouče, a znáte i okamžik, kdy se začne valit bez smýkání. Rychlost v tomto okamžiku tedy snadno zjistíte.
Nápověda 6c
Víte, jak se s časem mění rychlost těžiště kotouče. Zjistěte, jak se bude s časem měnit vzdálenost, kterou urazí. Okamžik, kdy se kotouč začne valit bez smýkání znáte. Vzdálenost uraženou do tohoto okamžiku pak snadno zjistíte.
Nápověda 7d
Práci třecí síly můžete spočítat dvojím způsobem.
Buď ze zákona zachování energie, kdy zjistíte rozdíl mechanické energie kotouče na začátku pohybu a v okamžiku, kdy se přestane smýkat. Úbytek mechanické energie je roven práci třecí síly.
Nebo lze vyjít přímo ze vztahu pro práci. Musíte ale ještě dopočítat prosmýkanou dráhu.
Řešení d)
Řešení 1:
Kinetická energie kotouče na začátku pohybu:
\[E_\mathrm{k0} = \frac{1}{2}m v_0^2\,.\]Kinetická energie kotouče v okamžiku, kdy se přestane smýkat:
\[E_\mathrm{k} = \frac{1}{2}m v_1^2 + \frac{1}{2}J \omega_1^2\,.\](Kotouč se posouvá a zároveň otáčí.)
Práce třecí síly je rovna rozdílu kinetických energií. Reálně se projeví zahřátím kotouče a podložky:
\[W = E_\mathrm{k0} - E_\mathrm{k} = \frac{1}{2}mv_0^2 -\frac{1}{2}mv_1^2-\frac{1}{2}J\omega_1^2\,.\]Dosadíme ze vztahů (6), (7), (8) a za moment setrvačnosti:
\(v_1=\frac{2v_0}{3}\,,\) \(\omega_1=\frac{2fgt_1}{R}\,,\) \(t_1=\frac{v_0}{3fg}\,,\) \(J=\frac{1}{2}mR^2\,.\)
Tedy:
\[W=\frac{1}{2}mv_0^2 - \frac{1}{2}m(\frac{2v_0}{3})^2-\frac{1}{2}(\frac{1}{2}mR^2)(\frac{2fg}{R}\cdot\frac{v_0}{3fg})^2 \,,\] \[W=\frac{1}{2}mv_0^2(1-(\frac{2}{3})^2-\frac{1}{2}(\frac{2}{3})^2)=\frac{1}{2}mv_0^2(1-\frac{6}{9})\,,\] \[W=\frac{1}{6}mv_0^2\,.\]Řešení 2:
Třecí síla je během smýkání konstantní, takže práci spočítáme ze vztahu:
\[W = F_\mathrm{t} x = mgfx\,,\]kde x je prosmýkaná dráha. Tu spočítáme jako rozdíl dráhy uražené těžištěm a provalené vzdálenosti:
\[x = s_1 - \alpha(t_1) R\] \[x = \frac{5}{18}\frac{v_0^2}{fg} - \frac{1}{2}\epsilon t_1^2 R\]Úhlové zrychlení známe \(\epsilon=\frac{2fg}{R} \), stejně jako čas t1:
\[x= \frac{5}{18}\frac{v_0^2}{fg} - \frac{1}{2}\frac{2fg}{R} (\frac{v_0}{3fg})^2 R = \frac{v_0^2}{fg}(\frac{5}{18}-\frac{1}{3^2})=\frac{3v_0^2}{18fg}\,,\] \[W = mgf\frac{3v_0^2}{18fg}= \frac{1}{6}mv_0^2\,.\]Celkové řešení
Hozený kotouč se po dopadu na podložku začne díky působení třecí síly postupně roztáčet. Po jistou dobu se však bude ještě také smýkat. Úhlová rychlost kotouče bude tedy postupně narůstat, zatímco rychlost posuvného pohybu těžiště bude klesat. Smýkání ustane v okamžiku, kdy bude platit, že rychlost těžiště kotouče je rovna součinu úhlové rychlosti otáčení kotouče a jeho poloměru.
Budeme tedy potřebovat napsat, jak se s časem mění rychlost těžiště kotouče a úhlová rychlost jeho otáčení. K tomu bude třeba zjistit, jaké síly na kotouč působí a jak ovlivňují jeho pohyb. K řešení posledního úkolu pak využijeme zákon zachování energie.
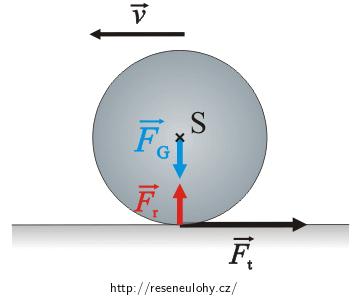
Na kotouč působí síla tíhová \(\vec{F}_\mathrm{G}\), tlaková síla podložky \(\vec{F}_\mathrm{r}\) a síla třecí \(\vec{F}_\mathrm{t}\).
Pro Ft platí:
\[F_\mathrm{t}=fF_\mathrm{G}=fmg\,.\tag{0}\](Nezávisí na rychlosti a po dobu smýkání zůstává stejná.)
Druhá impulsová věta říká:
\[\vec{M}=\frac{d\vec{L}}{dt}\,.\]V případě rotace tuhého tělesa kolem pevné osy platí:
\[L = J \omega\,,\] \[\vec{M}=\frac{d\vec{L}}{dt} = J\vec{\epsilon}\,,\]kde \(\vec{M}\) je výsledný moment sil působících na kotouč vzhledem ke zvolenému bodu, \(\vec{L}\) je celkový moment hybnosti vzhledem k tomuto bodu, \(J\) moment setrvačnosti kotouče vzhledem k pevné ose jdoucí zvoleným bodem a \(\vec{\epsilon}\) úhlové zrychlení kotouče.
Pro výsledný moment působících sil vzhledem ke středu kotouče S platí:
\[\vec{M}=\vec{R}\times\vec{F}_\mathrm{t} = J\vec{\epsilon}\,.\]Přepíšeme skalárně:
\[M = RF_\mathrm{t} = J\epsilon\,.\]Dosadíme za moment setrvačnosti a třecí sílu:
\[M = Rfmg = \frac{1}{2} mR^2\epsilon\,.\]Vyjádříme úhlové zrychlení kotouče:
\[\epsilon =\frac{2fg}{R}\,.\tag{1}\]Úhlové zrychlení kotouče je konstantní, pro jeho úhlovou rychlost pak platí:
\[\omega=\epsilon t\,.\tag{2}\](Počáteční úhlová rychlost byla nulová.)
Dosadíme za úhlové zrychlení:
\[\omega = \frac{2fgt}{R}\,.\tag{3}\]Pro těžiště kotouče platí:
\[\vec{F}_\mathrm{t} = m \vec{a}\,.\]Skalárně:
\[ -F_\mathrm{t} = ma\,.\]Dosadíme za třecí sílu ze vztahu (0) a vyjádříme zrychlení:
\[ -fmg = ma\,,\] \[a = -fg\,.\tag{4}\]Zrychlení je konstantní, těžiště se pohybuje rovnoměrně zpomaleným pohybem. Jeho počáteční rychlost byla v0. Platí tedy:
\[v = v_0+at\,.\]Dosadíme za zrychlení:
\[v = v_0- fgt\,.\tag{5}\]a) okamžik, kdy se kotouč začne pohybovat čistým valením
V okamžiku, kdy se kotouč přestane smýkat, platí:
\[v(t_1) = \omega (t_1)R\,.\]Dosadíme za v a ω ze vztahů (5) a (3):
\[v_0 - fgt_1 = \frac{2fgt_1}{R}R\,.\]Vyjádříme t1:
\[v_0 = 3fgt_1\,,\] \[ t_1 = \frac{v_0}{3fg}\,.\tag{6}\]b) rychlost těžiště kotouče
Využijeme znalosti času t1, kdy se kotouč přestane smýkat (6), a průběhu rychlosti těžiště (5). Stačí jen dosadit:
\[v_1 = v_0- fgt_1\,,\] \[v_1= v_0- fg\frac{v_0}{3fg}\,,\] \[v_1=\frac{2v_0}{3}\,.\tag{7}\]c) vzdálenost, kterou kotouč urazí
Zrychlení těžiště kotouče je konstantní. Pro vzdálenost, kterou urazí, platí:
\[s = v_0t + \frac{1}{2}at^2\,.\]Dosadíme za zrychlení ze vztahu (4):
\[s = v_0t - \frac{1}{2}fgt^2\,.\]V čase t1, kdy ustane smýkání, bude uražená vzdálenost:
\[s_1 = v_0t_1 - \frac{1}{2}fgt_1^2\,.\]Dosadíme za t1 ze vztahu (6):
\[s_1 = v_0\frac{v_0}{3fg} - \frac{1}{2}fg(\frac{v_0}{3fg})^2\,,\] \[s_1 = \frac{v_0^2}{3fg} - \frac{1}{2}\frac{v_0^2}{9fg}\,.\]Vytkneme \(\frac{v_0^2}{3fg}\):
\[s_1 = \frac{v_0^2}{3fg}(1-\frac{1}{6})\,,\] \[s_1 = \frac{5}{18}\frac{v_0^2}{fg}\,.\tag{8}\]d) práce třecí síly
Řešení 1:
Kinetická energie kotouče na začátku pohybu:
\[E_\mathrm{k0} = \frac{1}{2}m v_0^2\,.\]Kinetická energie kotouče v okamžiku, kdy se přestane smýkat:
\[E_\mathrm{k} = \frac{1}{2}m v_1^2 + \frac{1}{2}J \omega_1^2\,.\](Kotouč se posouvá a zároveň otáčí.)
Práce třecí síly je rovna rozdílu kinetických energií. Reálně se projeví zahřátím kotouče a podložky:
\[W = E_\mathrm{k0} - E_\mathrm{k} = \frac{1}{2}mv_0^2 -\frac{1}{2}mv_1^2-\frac{1}{2}J\omega_1^2.\]Dosadíme ze vztahů (6), (7), (8) a za moment setrvačnosti:
\(v_1=\frac{2v_0}{3}\,,\) \(\omega_1=\frac{2fgt_1}{R}\,,\) \(t_1=\frac{v_0}{3fg}\,,\) \(J=\frac{1}{2}mR^2\,.\)
Tedy:
\[W=\frac{1}{2}mv_0^2 - \frac{1}{2}m(\frac{2v_0}{3})^2-\frac{1}{2}(\frac{1}{2}mR^2)(\frac{2fg}{R}\cdot\frac{v_0}{3fg})^2 \,,\] \[W=\frac{1}{2}mv_0^2(1-(\frac{2}{3})^2-\frac{1}{2}(\frac{2}{3})^2)=\frac{1}{2}mv_0^2(1-\frac{6}{9})\,,\] \[W=\frac{1}{6}mv_0^2\,.\]Řešení 2:
Třecí síla je během smýkání konstantní, takže práci spočítáme ze vztahu:
\[W = F_\mathrm{t} x = mgfx\,,\]kde x je prosmýkaná dráha. Tu spočítáme jako rozdíl dráhy uražené těžištěm a provalené vzdálenosti:
\[x = s_1 - \alpha(t_1) R,\] \[x = \frac{5}{18}\frac{v_0^2}{fg} - \frac{1}{2}\epsilon t_1^2 R.\]Úhlové zrychlení známe \(\epsilon=\frac{2fg}{R} \), stejně jako čas t1:
\[x= \frac{5}{18}\frac{v_0^2}{fg} - \frac{1}{2}\frac{2fg}{R} (\frac{v_0}{3fg})^2 R = \frac{v_0^2}{fg}(\frac{5}{18}-\frac{1}{3^2})=\frac{3v_0^2}{18fg}\,,\] \[W = mgf\frac{3v_0^2}{18fg}= \frac{1}{6}mv_0^2\,.\]Odpověď
Kotouč se začne valit bez podkluzování po čase \(t_1=\frac{v_0}{3fg},\) v tom okamžiku má jeho těžiště rychlost \(v_1=\frac{2v_0}{3}\) a kotouč již urazil dráhu \(s_1=\frac{5}{18}\frac{v_0^2}{fg}.\)
Třecí síla za tu dobu vykonala práci \(W=\frac{1}{6}mv_0^2\,.\)


