Skluz tělesa po povrchu koule
Úloha číslo: 490
Z nejvyššího bodu koule s poloměrem R klouže bez tření malé těleso po povrchu koule dolů.
- A) V jaké hloubce h pod nejvyšším bodem se těleso oddělí od povrchu koule?
B) Určete rychlost tělesa v okamžiku oddělení od kulové plochy, jestliže mělo v nejvyšším bodě nulovou rychlost.
C) V jaké vzdálenosti od bodu dotyku koule s vodorovnou podložkou dopadne těleso na podložku?
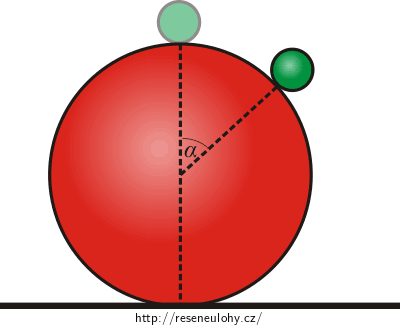
Nápověda 1A
Udělejte si náčrtek sil, které na těleso působí na vrcholu koule a pak na místě, kde očekáváte odloučení tělesa od povrchu koule.
Usnadní nám nějak práci, když tyto síly vhodně rozložíme?
Nápověda 2A
Napište pohybovou rovnici pro těleso a přepište ji skalárně.
Nápověda 3A
Vyjádřete cos α pomocí poloměru koule a hledané hloubky h.
Uvědomte si, jaký vztah platí pro normálové zrychlení tělesa.
Nápověda 4A
Vzhledem k tomu, že těleso po kouli klouže bez tření, můžete jeho rychlost v okamžiku oddělení určit ze zákona zachování mechanické energie.
Nápověda 5B
Velikost rychlosti tělesa v okamžiku oddělení je daná vztahem (5). Stačí dosadit.
Nyní určete, jaký úhel svírá vektor rychlosti s vodorovným směrem.
Nápověda 6C
O jaký typ pohybu půjde po oddělení tělesa od koule? Jak se bude s časem měnit vzdálenost, kterou urazí ve vodorovném a ve svislém směru?
Nápověda 7C
Z jaké výšky těleso padá? Jak dlouho trvá pád? Jakou vzdálenost přitom těleso urazí ve vodorovném směru?
Do konečného výsledku nezapomeňte započítat kolmou vzdálenost mezi místem, ve kterém se těleso oddělí, a bodem dotyku koule s podložkou.
Celkové řešení
A. V jaké hloubce pod nejvyšším bodem se těleso oddělí od povrchu koule?
Nakreslíme obrázek a vyznačíme působící síly:
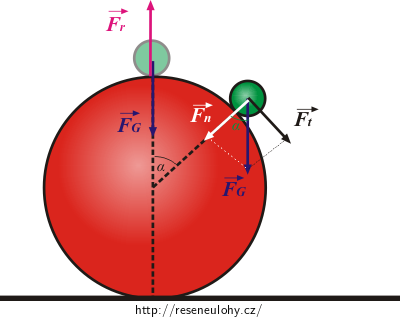
Na vrcholu koule:
\(\vec{F}_\mathrm{G}\) ..... tíhová síla,
\(\vec{F}_\mathrm{r}\) ..... síla, kterou tlačí koule do tělesa.
V místě oddělení:
(V okamžiku oddělení přestane koule do tělesa tlačit a síla \(\vec{F}_\mathrm{r}\) je nulová.)
Sílu \(\vec{F}_\mathrm{G}\) rozložíme do dvou složek:
normálové, směřující do středu koule....\(\vec{F}_\mathrm{n},\)
tečné, směřující ve směru rychlosti tělesa v okamžiku oddělení .... \(\vec{F}_\mathrm{t}.\)
Napíšeme pohybovou rovnici pro těleso a přepíšeme ji skalárně:
\[\vec{F}_\mathrm{r} + \vec{F}_\mathrm{G} = m\vec{a}\,.\]V okamžiku odpoutání tělesa od povrchu koule bude velikost síly Fr nulová, což nám vztah zjednoduší:
\[\vec{F}_\mathrm{G} = m\vec{a}\,.\]Přepíšeme skalárně:
ve směru tečném: \[F_\mathrm{G}\sin\alpha = ma_\mathrm{t},\tag{1}\]
ve směru normály: \[F_\mathrm{G}\cos\alpha = ma_\mathrm{n},\tag{2}\]
kde at je tečné a an normálové zrychlení.
Vyjádříme cosα pomocí poloměru koule a hledané hloubky h:
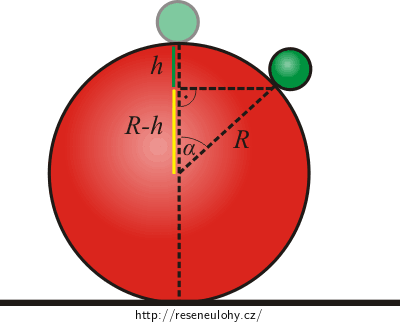
Z obrázku vyplývá, že:
\[\cos\alpha = \frac{R-h}{R}\,.\tag{3}\]Pro velikost dostředivého (normálového) zrychlení při pohybu po kružnici poloměru R platí: \(a_\mathrm{n} = \frac{v^2}{R}\,.\)
Dosadíme do rovnice (2):
\[mg\frac{R-h}{R} = m\frac{v^2}{R}\,.\]Odtud:
\[v^2 = g(R-h)\,.\tag{4}\]Vzhledem k tomu, že těleso po kouli klouže bez tření, můžeme jeho rychlost v okamžiku oddělení určit ze zákona zachování mechanické energie:
Hladinu nulové potenciální energie volíme v místě oddělení. Pak platí:
\[mgh = \frac{1}{2}mv^2\,.\]Odtud:
\[v^2 = 2gh\,.\tag{5}\]Dosadíme do vztahu (4):
\[2gh = g(R-h)\,,\] \[3h = R\,,\] \[h = \frac{R}{3}\,.\]
B. Jakou bude mít těleso v okamžiku odpoutání rychlost?
Velikost rychlosti tělesa je daná vztahem (5). Stačí dosadit. Ještě určíme, jaký úhel svírá vektor rychlosti s vodorovným směrem:
Dosadíme do vztahu (5):
\(v^2 = 2gh\); \(h = \frac{R}{3},\)
\[v = \sqrt{\frac{2}{3}gR}.\tag{6}\]
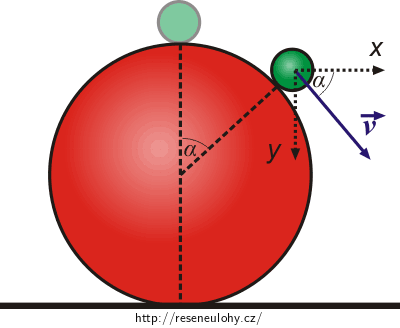
Z obrázku je patrné, že s vodorovným směrem svírá vektor rychlosti tělesa v okamžiku oddělení úhel α.
C. V jaké vzdálenosti od koule těleso dopadne?
Nejprve si uvědomíme, o jaký typ pohybu půjde po oddělení tělesa od koule a jak se bude s časem měnit vzdálenost, kterou urazí ve vodorovném a ve svislém směru.
Jedná se o vrh šikmý dolů. Ve vodorovném směru jde o rovnoměrný přímočarý pohyb, ve svislém směru o vrh svislý dolů. Souřadnice se s časem mění podle následujících vztahů:
\[x = v_\mathrm{x} t = vt\cos\alpha,\] \[y = v_\mathrm{y} t + \frac{1}{2}gt^2 = vt\sin\alpha + \frac{1}{2}gt^2.\]Podle (3):
\[\cos\alpha = \frac{R-h}{R} = \frac{R-\frac{R}{3}}{R} = \frac{2}{3}.\]S užitím Pythagorovy věty:
\[\sin\alpha = \frac{\sqrt{R^2 - (R-h)^2}}{R} = \frac{\sqrt{R^2 - \frac{4}{9}R^2}}{R} = \frac{\sqrt{5}}{3}.\]Dosadíme:
\[x = \frac{2}{3}vt,\tag{7}\] \[y = \frac{\sqrt{5}}{3}vt + \frac{1}{2}gt^2.\tag{8}\]Těleso padá z výšky \(\frac{5}{3}R.\)
Dobu pádu zjistíme ze vztahu (8), když uvážíme, jakou dráhu musí těleso během pádu urazit k podložce:
\[y = \frac{5}{3}R,\] \[\frac{5}{3}R = \frac{\sqrt{5}}{3}vt + \frac{1}{2}gt^2 = \frac{\sqrt{5}}{3}\sqrt{\frac{2}{3}gR}t + \frac{1}{2}gt^2.\]Upravíme:
\[\frac{1}{2}gt^2 + \frac{1}{3}\sqrt{\frac{10}{3}gR}t - \frac{5}{3}R = 0.\]Vynásobíme šesti:
\[3gt^2 + 2\sqrt{\frac{10}{3}gR}t - 10R = 0.\]Čas vyjádříme podle vzorce pro kořeny kvadratické rovnice a bereme v úvahu pouze kladný kořen – záporný čas nedává fyzikální smysl:
\[D = \frac{40}{3}gR + 120gR = \frac{400}{3}gR.\]Odtud pak:
\[t = \frac{-\sqrt{\frac{10}{3}gR} + 10\sqrt{\frac{1}{3}gR}}{3g}.\]Ve vodorovném směru těleso urazí podle vztahu (7) vzdálenost:
\[x = \frac{2}{3}vt = \frac{2}{3}\sqrt{\frac{2}{3}gR}(\frac{-\sqrt{\frac{10}{3}gR} + 10\sqrt{\frac{1}{3}gR}}{3g}).\]Roznásobíme a upravíme:
\[x = (\frac{20}{27}\sqrt{2} - \frac{4}{27}\sqrt{5})R =\frac{4}{27}R (5\sqrt{2} - \sqrt{5}).\]K této vzdálenosti musíme ještě přičíst vodorovnou vzdálenost, kterou těleso urazilo po povrchu koule:
\[d = R\sin\alpha = \frac{\sqrt{5}}{3}R.\] Výsledná vzdálenost tedy bude: \[L = x + d = \frac{4}{27}R (5\sqrt{2} - \sqrt{5}) + \frac{\sqrt{5}}{3}R = \frac{R}{3}(\frac{20\sqrt{2}}{9} -\frac{4\sqrt{5}}{9} + \sqrt{5}),\] \[L = \frac{5R}{27}(4\sqrt{2} + \sqrt{5}) \dot= 1{,}46 R.\]Odpověď
A) Těleso se oddělí od povrchu koule v hloubce rovné třetině poloměru koule:
\[h = \frac{R}{3}\,.\]B) Velikost rychlosti tělesa je ve chvíli oddělení:
\[v = \sqrt{\frac{2}{3}gR}\,.\]Vektor rychlosti tělesa svírá v okamžiku oddělení s vodorovným směrem úhel α.
C) Vzdálenost mezi bodem, kde se koule dotýká podložky, a bodem, kde těleso dopadne, je:
\[L = \frac{5R}{27}(4\sqrt{2} + \sqrt{5}) \dot= 1{,}46 R\,.\]





