Venturiho trubice
Úloha číslo: 1153
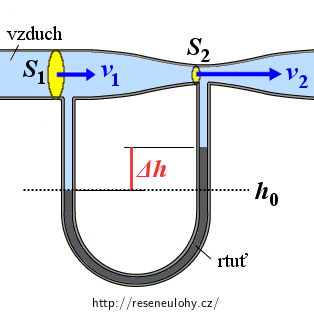
Do horizontálně umístěné Venturiho trubice vstupuje zprava rychlostí 15 m/s vzduch o hustotě 1,3 kg/m3. Poloměr širší části trubice je 1,0 cm, poloměr užší části 0,5 cm. Trubička tvaru U spojující širší a užší část hlavní trubice (viz obrázek) je naplněna rtutí o hustotě 13 600 kg/m3. Určete, jaký výškový rozdíl se ustálí mezi hladinami rtuti v U-trubičce.
Zápis
v1 = 15 m/s rychlost vstupujícího vzduchu r1 = 1,0 cm poloměr širší části trubice r2 = 0,5 cm poloměr užší části trubice ρ1 = 1,3 kg/m3 hustota vzduchu ρ2 = 13 600 kg/m3 hustota rtuti Δh = ? výškový rozdíl hladin v U-trubičce Nápověda 1
Co způsobuje různou výšku rtuti v ramenech U-trubičky?
Nápověda 2
Umíte rozdílný tlak vzduchu v ramenech U-trubičky matematicky propojit s hledaným rozdílem Δh? Pomozte si tím, že budete zkoumat velikost tlaku v úrovni nižší hladiny h0.
Nápověda 3
Nyní určíme rozdíl tlaků v čitateli výrazu (2). Vyjádřete jej z Bernoulliho rovnice, která popisuje ustálené proudění hlavní trubicí, a dosaďte do vztahu pro Δh.
Nápověda 4
Kterou veličinu ze vztahu (5) ještě stále neznáme? Použijte rovnici, která popisuje ustálené proudění tekutin a hledaná neznámá veličina se v ní vyskytuje. Vyjádřete tuto veličinu a dosaďte ji do vztahu (5).
Celkové řešení
Příčinou rozdílné výšky rtuti je různý tlak vzduchu nad její hladinou. V levém rameni je tlak vzduchu p1 vyšší a „zatlačuje“ tedy rtuť níže do trubice; naopak v pravém rameni je tlak vzduchu p2 nižší a rtuť tak může vystoupat výše. Protože ramena U-trubičky představují spojené nádoby, musí se v úrovni nižší hladiny h0 součet hydrostatického tlaku a tlaku vzduchu v obou ramenech rovnat. V našem případě tedy:
\[p_1\,=\,p_2\,+\,p_\mathrm{h},\tag{1}\]kde p1, p2 jsou tlaky vzduchu v ramenech U-trubičky a ph hydrostatický tlak rtuťového sloupce o výšce Δh. Do vztahu (1) dosadíme známou formuli pro velikost hydrostatického tlaku a vyjádříme hledaný rozdíl Δh:
\[p_1\,=\,p_2\,+\,{\Delta}h\varrho_2g\,\Rightarrow\,{\Delta}h\,=\,\frac{p_1\,-\,p_2}{\varrho_2g},\tag{2}\]kde ρ2 je hustota rtuti a g tíhové zrychlení.
Nyní je naším úkolem vyjádřit rozdíl tlaků v čitateli vztahu (2). K tomu použijeme Bernoulliho rovnici, která má pro ustálené proudění Venturiho trubicí tento tvar:
\[p_1\,+\,\frac{1}{2}{\varrho}_1v_1^2\,=\,p_2\,+\,\frac{1}{2}{\varrho}_1v_2^2,\tag{3}\]kde levá strana rovnice popisuje místo o průřezu trubice S1 a pravá strana místo o průřezu trubice S2. Přitom v1, v2 jsou rychlosti proudícího vzduchu v těchto místech a ρ1 hustota vzduchu. (Protože trubice je ve vodorovné poloze, nemusíme v Bernoulliho rovnici uvažovat změny potenciální energie proudícího vzduchu.) Pro námi hledaný rozdíl tlaků tedy platí:
\[p_1\,-\,p_2\,=\,\frac{1}{2}{\varrho}_1(v_2^2\,-\,v_1^2).\tag{4}\]Dosazením tohoto vztahu do rovnice (2) dostáváme:
\[{\Delta}h\,=\,\frac{{\varrho}_1(v_2^2\,-\,v_1^2)}{2{\varrho}_2g}.\tag{5}\]Poslední neznámou veličinou ve vztahu (5) je nyní rychlost vzduchu v2 v místě o průřezu S2. K určení této rychlosti použijeme rovnici kontinuity pro ustálené proudění:
\[S_1v_1\,=\,S_2v_2.\tag{6}\]Protože předpokládáme kruhový průřez trubice, můžeme za obsahy S1, S2 dosadit a vyjádřit rychlost v2:
\[{\pi}r_1^2v_1\,=\,{\pi}r_2^2v_2\,\Rightarrow\,v_2\,=\,v_1\frac{r_1^2}{r_2^2},\tag{7}\]kde r1, r2 jsou zadané poloměry příslušných částí trubice. Vypočítanou rychlost nyní dosadíme do vztahu (5) a dostáváme:
\[{\Delta}h\,=\,\frac{{\varrho}_1}{2{\varrho}_2g}((v_1\frac{r_1^2}{r_2^2})^2\,-\,v_1^2)\,=\,\frac{{\varrho}_1v_1^2}{2{\varrho}_2g}(\frac{r_1^4}{r_2^4}\,-\,1).\tag{8}\]Číselně:
\[{\Delta}h\,=\,\frac{1{,}3{\cdot}15^2}{2{\cdot}13\,600{\cdot}9{,}81}(\frac{0{,}010^4}{0{,}005^4}\,-\,1)\,\mathrm{m}\,=\,0{,}016\,\mathrm{m}\,=\,1{,}6\,\mathrm{cm}.\]Rozdíl mezi výškou hladin rtuti v ramenech U-trubičky je přibližně 1,6 cm.
Odpověď
\[{\Delta}h\,=\,\frac{{\varrho}_1v_1^2}{2{\varrho}_2g}(\frac{r_1^4}{r_2^4}\,-\,1)\]Rozdíl mezi výškou hladin rtuti v ramenech U-trubičky je přibližně 1,6 cm.
Použití Venturiho trubice
V praxi se Venturiho trubice využívá u letadel k měření rychlosti letu. Poskytuje přesnější měření než například častější Pitotova trubice, ale je určena spíše pro menší rychlosti letu – v zúženém místě se totiž již při malých rychlostech dosahuje rychlosti zvuku.





