Měření rychlosti světla
Úloha číslo: 213
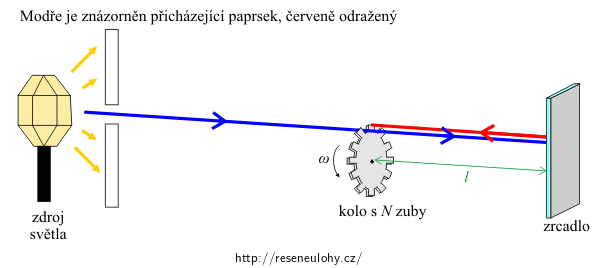
Jedna z metod měření světla používala rovnoměrně otáčející se ozubené kolo (viz obrázek). Světelný paprsek prošel mezerou mezi zuby kola, odrazil se od zrcadla, vracel se po stejné dráze a dopadl zpět na kolo tak, že narazil do následujícího zubu (tj. za kolo už neprošel). Na obvodu ozubeného kola bylo 720 zubů. Vzdálenost kola a zrcadla byla 9 km. Tuto metodu objevil a použil roku 1849 A. H. L. Fizeau.
Naměřil hodnotu rychlosti světla 313 000 km·s−1.
a) Jaká byla úhlová rychlost ozubeného kola?
b) Předpokládejte, že poloměr kola byl 5 cm. Jaká je velikost rychlosti bodu na obvodu takového kola?
Zápis
N = 720 počet zubů na obvodu kola l = 9 km vzdálenost kola a zrcadla c = 313 000 km·s−1 naměřená rychlost světla ω = ? (rad·s−1) úhlová rychlost otáčení kola r = 5 cm poloměr kola v = ? (m·s−1) rychlost bodu na obvodu kola Nápověda 1 – vztah pro úhlovou rychlost ω
Vaším cílem je určit úhlovou rychlost ω. Vzpomenete si, jakým vztahem je definována? Jaké veličiny tedy potřebujete znát?
Nápověda 2 – vyjádření času Δt
Umíte vyjádřit čas Δt, za který doletí paprsek od kola k zrcadlu a zpátky?
Nápověda 3 – vyjádření potočení Δφ
O jaký úhel Δφ se za tuto dobu Δt kolo pootočí, má-li se paprsek, který prošel mezerou mezi dvěma zuby, při cestě zpět o jeden z těchto zubů zastavit?
Na úvod použijte dílčí úvahu – o jaký úhel by se kolo muselo pootočit, aby se paprsek při cestě k zrcadlu a zpět „trefil“ do dvou po sobě jdoucích mezer?
Nápověda 4 – výpočet úhlové rychlosti ω
Zkombinujte výše uvedené vztahy a vypočítejte úhlovou rychlost ω.
Nápověda 5 – výpočet rychlosti v bodu na obvodu
Jak nyní z úhlové rychlosti kola ω vypočítáte rychlost bodu v na jeho obvodu? Znáte poloměr kola r.
Celkové řešení
a) Úhlová rychlost ω je definována jako:
\[\omega\,=\,\frac{{\Delta}\varphi}{{\Delta}t}\,,\tag{1}\]kde Δφ je změna úhlové dráhy (v případě našeho kola je to nějaké „pootočení“) za čas Δt.
Potřebujeme tedy vědět, o jaký úhel se kolo pootočí za nějaký charakteristický čas.
Při cestě od ozubeného kola k zrcadlu a zpět se paprsek pohybuje rychlostí c a urazí dráhu 2l. Na svoji cestu potřebuje čas:
\[{\Delta}t\,=\,\frac{2l}{c}\,.\tag{2}\]Máme-li na obvodu kola N zubů, máme na něm i N mezer. Má-li se kolo otočit o 1 mezeru (nebo o 1 zub), musí se pootočit o úhel Δφ0:
\[\Delta\varphi_0\,=\,\frac{2\pi}{N}\,.\]V naší úloze nepotřebujeme otočení o celou mezeru, ale pouze o polovinu mezery – tj. o vzdálenost mezera–zub. Proto pro hledaný úhel Δφ bude platit:
\[\Delta\varphi\,=\,\frac{1}{2}\Delta\varphi_0\,=\,\frac{1}{2}{\cdot}\frac{2\pi}{N}\,=\,\frac{\pi}{N}\,.\tag{3}\]Ze vztahů (2) a (3) dosadíme do definičního vztahu (1):
\[\omega\,=\,\frac{\Delta\varphi}{{\Delta}t}\,=\,\frac{\frac{\pi}{N}}{\frac{2l}{c}}\,=\,\frac{{\pi}c}{2lN}\,.\] Číselně: \[c\,=\,313000\,\mathrm{km{\cdot}s^{-1}}\,=\,3{,}13{\cdot}10^8\,\mathrm{m{\cdot}s^{-1}},\] \[N\,=\,720,\] \[l\,=\,9\,\mathrm{km},\] \[\omega\,=\,(\frac{{\pi}{\cdot}{3{,}13{\cdot}10^8}}{2{\cdot}9000{\cdot}720})\,\mathrm{rad{\cdot}s^{-1}}\,\dot{=}\,75{,}9\,\mathrm{rad{\cdot}s^{-1}}.\]b) Rychlost bodu na obvodu kola o poloměru r a úhlové rychlosti ω lze vyjádřit jako:
\[v\,=\,{\omega}r\,.\]Číselně:
\[\omega\,=\,75{,}9\,\mathrm{rad{\cdot}s^{-1}},\] \[r\,=\,5\,\mathrm{cm}\,=\,0{,}05\,\mathrm{m},\]
\[v\,=\,{\omega}r\,\dot{=}\,(75{,}9{\cdot}0{,}05)\,\mathrm{m{\cdot}s^{-1}}\,\dot{=}\,3{,}8\,\mathrm{m{\cdot}s^{-1}}.\]Výsledek
a) Kolo se otáčí s úhlovou rychlostí \[\omega\,=\,\frac{{\pi}c}{2lN}\,\dot{=}\,75{,}9\,\mathrm{rad{\cdot}s^{-1}}\,.\]
b) Body na jeho obvodu mají rychlost \[v\,=\,{\omega}r\,\dot{=}\,3{,}8\,\mathrm{m{\cdot}s^{-1}}\,.\]


