Plování skleněné trubice
Úloha číslo: 1035
Skleněná trubice ve tvaru dutého válce o vnějším průměru 40 mm má délku 1 m. Trubice je naplněna vzduchem a na obou koncích uzavřena zátkami. Určete, jaký je vnitřní průměr trubice, jestliže se tato ve vodě volně vznáší. Hustota použitého skla je 2500 kg·m-3, hmotnost zátek a vzduchu uvnitř trubice zanedbejte.
Zápis
d1 = 40 mm = 0,040 m vnější průměr trubice l = 1 m délka trubice ρs = 2500 kg·m−3 hustota skla d2 = ? vnitřní průměr trubice Nápověda 1
Nakreslete si obrázek. Jaké síly na trubici ponořenou ve vodě působí a jaký mají směr? Co pro tyto síly platí, víte-li, že se trubice ve vodě volně vznáší?
Nápověda 2 – určení tíhové síly
Určete velikost tíhové síly působící na trubici. Jak si poradíte s tím, že neznáte hmotnost trubice? Využijte definiční vztah pro hustotu. I po jeho použití ale ve vztahu pro tíhovou sílu zbyde veličina, jež není explicitně zadaná – která?
Nápověda 3 – určení tíhové síly
K určení objemu skla, ze kterého je trubice vyrobená (potřebného k výpočtu tíhové síly), budete muset spočítat objemy dvou válců. Jakých? Kde je v obrázku najdete? Výsledný objem skla dosaďte do vztahu pro tíhovou sílu.
Nápověda 4 – určení vztlakové síly
Nyní určete vztlakovou sílu působící na trubici. Ve vztahu pro její výpočet vystupuje objem – bude to stejný objem jako ve výpočtu tíhové síly? Uvědomte si, že trubice je na obou koncích uzavřena zátkami.
Nápověda 5
Velikost tíhové a vztlakové síly položte do rovnosti dle vztahu (1) a vyjádřete vnitřní průměr trubice d2. Číselně dopočítejte.
Celkové řešení
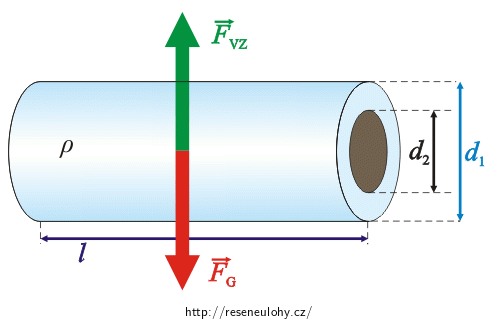
Na trubici působí:
- tíhová síla FG směrem svisle dolů,
- vztlaková síla Fvz směrem svisle vzhůru.
Jestliže se trubice ve vodě volně vznáší (tj. je v klidu), je výsledná síla na ni působící nulová, tedy:
\[\vec{F}_\mathrm{G}\,+\,\vec{F}_\mathrm{vz}\,=\,\vec{o}\,.\]Protože výše uvedené dvě síly mají opačný směr, lze pro jejich velikosti psát:
\[F_\mathrm{G}\,-\,F_\mathrm{vz}\,=\,0\,\Rightarrow\,F_\mathrm{G}\,=\,F_\mathrm{vz}\,.\tag{1}\]Při určování tíhové síly působící na trubici vyjdeme ze známého vztahu:
\[F_\mathrm{G}\,=\,mg\,,\tag{2}\]kde m je hmotnost trubice a g tíhové zrychlení. Neznáme sice hmotnost trubice m, ale je zadána hustota skla ρs, ze kterého je trubice vyrobena. Hmotnost m tedy vyjádříme z definičního vztahu pro hustotu:
\[{\rho_\mathrm{s}}\,=\,\frac{m}{V}\,\Rightarrow\,m\,=\,{\rho_\mathrm{s}}V\,,\tag{3}\]kde V je objem skla, ze kterého je trubice vyrobená. Spojením vztahů (2) a (3) dostáváme pro tíhovou sílu:
\[F_\mathrm{G}\,=\,{\rho_\mathrm{s}}Vg\,.\tag{4}\]Stále ovšem neznáme objem skla, ze kterého je trubice vyrobená. Žádný obecně známý vztah nám sice neříká, jak jej počítat, snadnou úvahou jej ale určíme. V našem obrázku si představte dva válce:
- Větší válec (objem V1) o výšce l a poloměru podstavy d1.
- Menší válec (objem V2) o výšce rovněž l a poloměru podstavy d2.
Z obrázku je ihned patrné, že objem skla, ze kterého je trubice vyrobená, je roven rozdílu objemů V1 a V2, tedy:
\[V\,=\,V_1\,-\,V_2\,.\tag{5}\]Za pomoci vztahu pro objem válce pak platí:
\[V\,=\,{\pi}(\frac{d_1}{2})^2l\,-\,{\pi}(\frac{d_1}{2})^2l\,=\,\frac{{\pi}l}{4}(d_1^2\,-\,d_2^2)\,.\tag{6}\]Dosazením do vztahu (4) konečně dostáváme finální vztah pro výpočet tíhové síly:
\[F_\mathrm{G}\,=\,{\rho_\mathrm{s}}\frac{{\pi}l}{4}(d_1^2\,-\,d_2^2)g\,.\tag{7}\]Vztlakovou sílu určíme podle známého vztahu:
\[F_\mathrm{vz}\,=\,V'{\rho}g\,,\tag{8}\]kde V´ je objem vymezený ponořenou trubicí, ρ hustota kapaliny (zde tedy vody) a g tíhové zrychlení. Je třeba si uvědomit, že objem vymezený ponořenou trubicí zahrnuje jak objem V vlastní trubice (určený vztahem (6)), tak objem její dutiny – jde tedy o válec výšky l s poloměrem podstavy d1:
\[V'\,=\,{\pi}(\frac{d_1}{2})^2l\,.\tag{9}\]Dosazením do vztahu (8) pro vztlakovou sílu:
\[F_\mathrm{vz}\,=\,{\pi}(\frac{d_1}{2})^2l{\rho}g\,.\tag{10}\]Nyní máme k dispozici obecné vyjádření velikosti obou sil, které dle vztahu (1) položíme do rovnosti. Dosazením (7) a (10) do (1) dostáváme:
\[{\rho_\mathrm{s}}\frac{{\pi}l}{4}(d_1^2\,-\,d_2^2)g\,=\,{\pi}(\frac{d_1}{2})^2l{\rho}g\,,\] \[{\rho_\mathrm{s}}\frac{{\pi}l}{4}(d_1^2\,-\,d_2^2)\,=\,\frac{{\pi}l}{4}d_1^2{\rho}\,,\] \[{\rho_\mathrm{s}}(d_1^2\,-\,d_2^2)\,=\,d_1^2{\rho}\,,\] \[d_1^2 (\rho_\mathrm{s}-\rho) = \rho_s d_2^2\,,\] \[d_2\,=\,d_1\sqrt{1\,-\,\frac{\rho}{\rho_\mathrm{s}}}\,.\]Číselně:
\[d_2\,=\,0{,}040\sqrt{1\,-\,\frac{1000}{2500}}\,\mathrm{m}\,\dot=\,31\,\mathrm{mm}\,.\]Odpověď
Vnitřní průměr trubice je asi 31 mm.





