Princip Pitotovy trubice

Úloha číslo: 1038

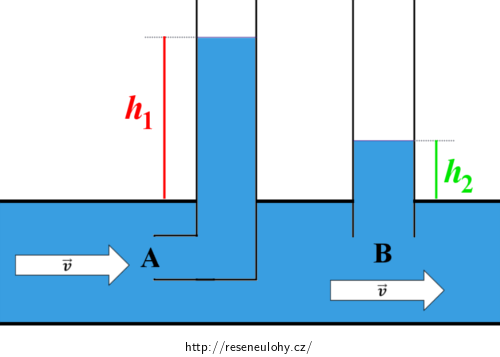
Do vodorovného potrubí jsou vložené dvě manometrické trubice; jedna z nich je rovná, druhá ohnutá do pravého úhlu a obrácená otvorem proti směru proudění kapaliny. Jaká je rychlost tohoto proudění, jestliže v rovné trubici vystoupila voda do výšky 10 cm a v ohnuté trubici do výšky 30 cm?

Zápis

h₁ = 30 cm = 0,30 m výška hladiny v zahnuté trubici

h₂ = 10 cm = 0,10 m výška hladiny v rovné trubici

v = ? rychlost proudící kapaliny
Nápověda 1
Zadání se nás ptá na rychlost proudící vody. Vybavíte si nějaký fyzikální vztah, který se věnuje proudění kapalin a přitom se v něm pracuje s rychlostí? Prozradíme, že další veličinou, která ve vztahu vystupuje, je tlak.
Řešení nápovědy 1
Proudění kapaliny vodorovným potrubím nejjednodušeji popisuje Bernoulliho rovnice, která má tvar:
\[\frac{1}{2}{\rho_\mathrm{k}}v_\mathrm{k}^2\,+\,p\,=\,konst.\tag{1}\]
kde ρ_k je hustota proudící kapaliny, v_k její rychlost a p tlak v kapalině v daném místě potrubí.

(Připomeňte si odvození této rovnice – jde vlastně o zákon zachování mechanické energie pro ustálené proudění ideální kapaliny vztažený na jednotkový objem kapaliny.)
Nápověda 2
Použijte Bernoulliho rovnici na náš příklad – rozepište výraz na levé straně vztahu (1) pro ústí ohnuté trubice (bod A) i ústí rovné trubice (bod B). Uvědomte si, že tento součet zůstává pro dané vodorovné potrubí konstantní.
Řešení nápovědy 2
Označíme v₁ rychlost proudění v bodě A a p₁ tlak v bodě A, v₂ rychlost proudění v bodě B a p₂ tlak v bodě B. Podle Bernoulliho rovnice platí:
\[\frac{1}{2}{\rho}v_1^2\,+\,p_1\,=\,\frac{1}{2}{\rho}v_2^2\,+\,p_2\,,\tag{2}\]
kde ρ je hustota vody. Levá část rovnosti popisuje proudění v bodě A, pravá strana proudění v bodě B.
Nápověda 3
Jaká je rychlost proudění v₁ v bodě A? Zjednodušte Bernoulliho rovnici ze (2). Které veličiny zbývá ještě určit?
Řešení nápovědy 3
Jakmile se kapalina dostane k ústí zahnuté trubice, zastaví se, tj. v₁ = 0 m·s^-1. Ve vztahu (2) zůstává tedy pouze jediná nenulová rychlost v₂ = v a tento vztah lze potom přepsat jako:
\[p_1\,=\,\frac{1}{2}{\rho}v^2\,+\,p_2\,.\tag{3}\]
Abychom rychlost v proudění určili, potřebujeme znát velikost tlaků p₁, p₂.
Nápověda 4
Jakým způsobem určíme tlak v místech A a B? Uvědomte si, které zadané údaje jsme zatím nevyužili.
Řešení nápovědy 4
Máme zadánu výšku vody h₁, h₂ v obou manometrických trubicích, což nám umožňuje počítat tlak p₁, resp. p₂ jako hydrostatický tlak vodního sloupce v trubici – na tomto principu je koneckonců manometrické měření tlaku založeno. Ze známého vztahu pro hydrostatický tlak dostáváme:
\[p_1\,=\,h_1{\rho}g\,,\tag{4}\] \[p_2\,=\,h_2{\rho}g\,,\tag{5}\]
kde ρ je hustota vody a g tíhové zrychlení.
Nápověda 5
Dosaďte ze vztahů (4) a (5) do rovnice (2) a vyjádřete hledanou rychlost v. Dopočítejte číselně.
Řešení nápovědy 5
Dosazením vztahů (4) a (5) do rovnice (3) dostáváme:
\[h_1{\rho}g\,=\,\frac{1}{2}{\rho}v^2\,+\,h_2{\rho}g\,,\] \[h_1g\,=\,\frac{1}{2}v^2\,+\,h_2g\,,\] \[v\,=\,\sqrt{2g(h_1\,-\,h_2)}\,.\]
Číselně:
\[v\,=\,\sqrt{2{\cdot}9{,}81(0{,}30\,-\,0{,}10)}\,\mathrm{m}{\cdot}\mathrm{s}^{-1}\,\dot=\,2\,\mathrm{m}{\cdot}\mathrm{s}^{-1}\,.\]
Použití tohoto jevu – Pitotova trubice
Konstrukce popsaná na obrázku k této úloze našla uplatnění zejména v leteckém průmyslu při konstrukci rychloměrů letadel. Proudícím médiem není kapalina, ale vzduch a zjednodušeně lze říci, že z rozdílu tlaků v rovné a ohnuté trubici lze určit rychlost letadla.
Celkové řešení
Proudění kapaliny vodorovným potrubím nejjednodušeji popisuje Bernoulliho rovnice, která má tvar:
\[\frac{1}{2}{\rho_\mathrm{k}}v_\mathrm{k}^2\,+\,p\,=\,konst.\tag{1}\]
kde ρ_k je hustota proudící kapaliny, v_k její rychlost a p tlak v kapalině v daném místě potrubí. (Jde vlastně o zákon zachování mechanické energie pro ustálené proudění ideální kapaliny vztažený na jednotkový objem kapaliny.)

Označíme v₁ rychlost proudění v bodě A a p₁ tlak v bodě A, v₂ rychlost proudění v bodě B a p₂ tlak v bodě B. Podle Bernoulliho rovnice platí:
\[\frac{1}{2}{\rho}v_1^2\,+\,p_1\,=\,\frac{1}{2}{\rho}v_2^2\,+\,p_2\,,\tag{2}\]
kde ρ je hustota vody. Levá část rovnosti popisuje proudění v bodě A, pravá strana proudění v bodě B.

Jakmile se kapalina dostane k ústí zahnuté trubice, zastaví se, tj. v₁ = 0 m·s^-1. Ve vztahu (2) zůstává tedy pouze jediná nenulová rychlost v₂ = v a tento vztah lze potom přepsat jako:
\[p_1\,=\,\frac{1}{2}{\rho}v^2\,+\,p_2\,.\tag{3}\]
Máme zadánu výšku vody h₁, h₂ v obou manometrických trubicích, což nám umožňuje počítat tlak p₁, resp. p₂ jako hydrostatický tlak vodního sloupce v trubici – na tomto principu je koneckonců manometrické měření tlaku založeno. Ze známého vztahu pro hydrostatický tlak dostáváme:
\[p_1\,=\,h_1{\rho}g\,,\tag{4}\] \[p_2\,=\,h_2{\rho}g\,,\tag{5}\]
kde ρ je hustota vody a g tíhové zrychlení.

Dosazením vztahů (4) a (5) do rovnice (3) dostáváme:
\[h_1{\rho}g\,=\,\frac{1}{2}{\rho}v^2\,+\,h_2{\rho}g\,,\] \[h_1g\,=\,\frac{1}{2}v^2\,+\,h_2g\,,\] \[v\,=\,\sqrt{2g(h_1\,-\,h_2)}\,.\]
Číselně:
\[v\,=\,\sqrt{2{\cdot}9{,}81(0{,}30\,-\,0{,}10)}\,\mathrm{m}{\cdot}\mathrm{s}^{-1}\,\dot=\,2\,\mathrm{m}{\cdot}\mathrm{s}^{-1}\,.\]
Odpověď
Rychlost proudění vody v potrubí je přibližně 2 m·s^-1.