Kmitání nádoby s kuličkou

Úloha číslo: 4500

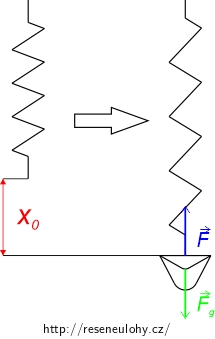
Nádobu o hmotnosti 400 g zavěsíme na lehkou pružinu s koeficientem tuhosti pružiny 1,0 N·cm^-1.

a) Vypočítejte, o kolik se pružina prodlouží, zavěsíme-li na ni nádobu.

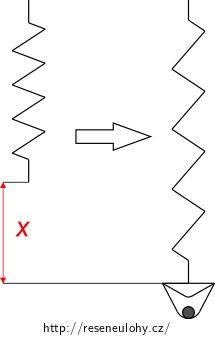
b) Do nádoby, která je v klidu, položíme kouli o hmotnosti 1,5 kg. Nádoba s koulí se rozkmitá. Pomocí výpočtu ukažte, že amplituda, s kterou nádoba s koulí kmitá, je 15 cm.

c) Vypočítejte dobu kmitu a maximální zrychlení nádoby s koulí během kmitání.

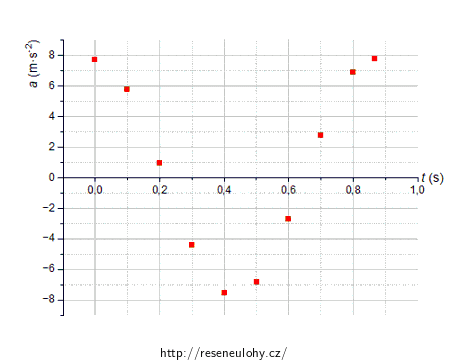
d) Do systému souřadnic nakreslete graf závislosti zrychlení nádoby s koulí na čase pro jeden kmit začínající v dolní krajní poloze. Označte si osy, použijte vhodné měřítko na osách v jednotkách m·s^-2 a s. Směr zrychlení nahoru považujte za kladný.

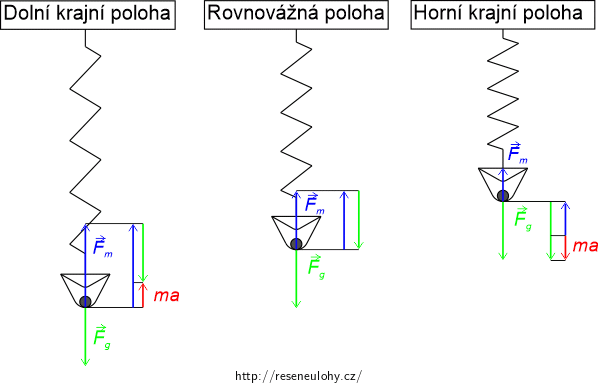
e) Spočítejte sílu, kterou v nejnižší poloze působí koule na dno nádoby.

f) Vypočítejte amplitudu, s kterou může nádoba s koulí kmitat tak, aby se koule i ve svojí nejvyšší krajní poloze stále dotýkala nádoby.

Zápis

m₀ = 400 g	hmotnost nádoby
k = 1,0 N·cm^-1	tuhost pružiny
m = 1,5 kg	hmotnost koule
a) x₀ = ?	prodloužení pružiny po zavěsení nádoby
b) x_A = ?	amplituda kmitů po vložení koule do nádoby
c) T = ?	doba kmitu nádoby s kuličkou
a = ?	maximální zrychlení nádoby s kuličkou
e) F_m = ?	síla, kterou v nejnižší poloze působí koule na dno nádoby
f) x_m = ?	amplituda, pro kterou se bude koule ve své nejvyšší krajní poloze dotýkat dna nádoby

Nápověda a: prodloužení pružiny
Po zavěsení nádoby se pružina prodlouží. Popiš všechny síly působící na nádobu v rovnovážné poloze. Jaký budou mít směr a velikost? Co pro ně musí platit?
Řešení nápovědy a: prodloužení pružiny
Nádoba bude v rovnovážné poloze, kde výslednice sil působících na pružinu je nulová. Bude na ní působit síla pružnosti F = kx a tíhová síla F_G = mg. Aby výslednice byla nulová, musí mít síly stejnou velikost a opačný směr. Pružina se po zavěsení nádoby prodlouží o:
\[F = kx_0 = m_0g \rightarrow x_0 = \frac{m_0g}{k} = \frac{4{\cdot} 10^{-1} \ \text{kg} \cdot 9{,}81 \ \text{m}\cdot \text{s}^{-2}}{1 \ \text{N}\cdot \text{cm}^{-1}} \dot = 3{,}9 \ \text {cm}.\]
Nápověda b: amplituda kmitu
Amplituda je v našem případě maximální výchylka kmitající nádoby s koulí. Toto maximum musíme vůči něčemu počítat, konkrétně vzhledem k nové rovnovážné poloze nádoby s koulí. Kde bude nová rovnovážná poloha (co pro ni musí platit)? Do jaké maximální výšky vykmitne nádoba s koulí? Dokážete z těchto dvou informací určit amplitudu kmitů?
Řešení nápovědy b: amplituda kmitu
Pro novou rovnovážnou polohu nádoby s koulí musí platit:
\[F = kx = (m + m_0)g \]
Nové rovnovážné poloze nádoby s koulí tedy odpovídá prodloužení:
\[x = \frac{(m + m_0)g}{k} \]

Původní prodloužení pružiny jen s nádobou je x₀. Tato původní poloha bude zároveň nejvyšší polohou kmitů pružiny po přidání koule (výš už nádoba s koulí při kmitání vystoupat nemůže kvůli zákonu zachování energie).

Amplitudu, s kterou nádoba s koulí kmitá, označíme x_A (vzdálenost krajní a rovnovážné polohy):
\[ x_A = x - x_0 = \frac{(m + m_0)g}{k} - \frac{m_0g}{k} = \frac{mg}{k} = \frac{1{,}5 \ \text{kg} \cdot 9{,}81 \ \text{m}\cdot \text{s}^{-2}}{1 \ \text{N}\cdot \text{cm}^{-1}} \dot= 14{,}7 \ \text{cm} \]
Nápověda c: perioda kmitání
Připomeňte si, jaký je vztah pro periodu kmitu pružiny se závažím.

V jaké poloze bude zrychlení kmitající nádoby s koulí maximální? Tíhová síla zůstává konstantní, jak to tedy bude souviset s výchylkou?
Řešení nápovědy c: perioda a maximální zrychlení
Pro periodu kmitání nádoby s koulí platí:
\[T = 2\pi \sqrt{\frac{m + m_0}{k}} = 2\pi \cdot \sqrt{\frac{1{,}9 \ \text{kg}}{100 \ \text{N}/\text{m}}} \dot= 0{,}87 \ \text{s}.\]
Maximální zrychlení bude v polohách, kdy je výsledná síla působící na nádobu s koulí maximální. Víme, že v rovnovážné poloze je výslednice nulová, tíhová síla zůstává konstantní, mění se pouze síla pružnosti pružiny. Když bude síla pružnosti pružiny maximální, tak bude výslednice sil maximální. Tomu odpovídají krajní polohy. V dolní krajní poloze bude výslednice:
\[F = k(x+x_A) - mg = k x_A\]
V horní krajní poloze bude mít výslednice sil opačný směr, ale stejnou velikost.

Pro výslednou sílu platí:
\[F = (m + m_0)a \ \land \ F = k x_A \rightarrow a = \frac{k}{m + m_0} x_A\] \[a = \frac{1 \ \text{N}\cdot \text{cm}^{-1}}{0{,}4 \ \text{kg} + 1{,}5 \ \text{kg}}\cdot 14{,}7 \ \text{cm} \dot= 7{,}74 \ \text{m}\cdot \text{s}^{-2}.\]
Nápověda d: graf zrychlení
Jediné, co pro vyřešení této úlohy potřebujeme, je znát závislost okamžitého zrychlení kmitavého pohybu na čase, pak už budeme pouze vynášet hodnoty do grafu. Připomeňte si tento vztah, případně si ho vyhledejte v literatuře či na webu.

Poznámka
Pokud znáte vztah pro okamžitou výchylku kmitavého pohybu, můžete si vztah pro zrychlení spočítat.
\[y = y_m \cos(\omega t)\]
Derivací okamžité výchylky získáme závislost rychlosti kmitající nádoby na čase
\[y' = v = -\omega y_m\sin(\omega t)\]
Derivací rychlosti dojdeme ke vztahu pro zrychlení kmitající nádoby.
\[v' = a = -\omega^2y_m\cos(\omega t)\]
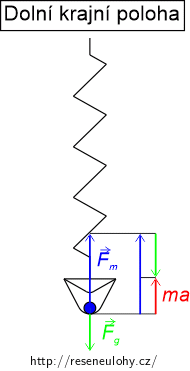
Nápověda e: síla v nejnižší poloze
Uvědomte si nejprve, jaké všechny síly působí na kouli v nejnižším bodě a jaká je jejich výslednice.

Vyjádřete si sílu, kterou nádoba působí na kouli. K určení síly, kterou tlačí koule do dna nádoby, použijte 3. Newtonův zákon.
Řešení nápovědy e: Síla na dno nádoby
Na kouli působí v nejnižším bodě tíhová síla F_G = mg směrem dolů. Směrem nahoru do ní tlačí silou F_m nádoba. Koule se začíná pohybovat nahoru se zrychlením a. (Pozor, pružina sama o sobě na kouli nepůsobí, pružina působí na misku a právě ta působí na kouli).

Výsledná síla působící na kouli je tedy: \(F_m - F_g = ma.\)

Velikost síly, kterou v nejnižší poloze do koule tlačí nádoba, je podle 3. Newtonova zákonu rovna velikosti síly, kterou tlačí koule na dno nádoby. Rovná se
\[F_m = m(a + g) = 1{,}5 \ \text{kg} \cdot (9{,}81 + 7{,}74)\ \text{m}\cdot \text{s}^{-2} \dot= 26{,}3 \ \text{N}.\]
Nápověda f: amplituda a dotyk
V průběhu kmitání působí na kouli tíhová síla, její velikost se nemění. Dále do koule tlačí nádoba. Uvědomte si, jak se v průběhu kmitání tato síla mění. Kdy je největší, kdy bude nejmenší? Jak velká by byla tato síla v okamžiku, kdy by se koule přestala misky dotýkat?
Řešení nápovědy f: amplituda a dotyk
Nádoba tlačí do koule nejvíce v krajní dolní poloze. V průběhu pohybu vzhůru se tlaková síla nádoby zmenšuje, v rovnovážné poloze se vyrovná s tíhovou silou a pak dále klesá. Nejmenší je v horní krajní poloze. V situaci, kdy by se koule přestávala dna nádoby dotýkat, by byla tato síla nulová.

Výsledná síla působící na kouli v horní krajní poloze je:
\[F = F_g - F_m\] V hraničním případě bude F_m rovna nule, pak: \[F = ma \rightarrow ma = mg \rightarrow a = g \]
V horní krajní poloze je zrychlení kmitavého pohybu maximální a platí pro něj:
\[a = \omega^2x_m = \left(\frac{2\pi}{T}\right)^2x_m\]
Pak:
\[g= \left(\frac{2\pi}{T}\right)^2x_m\]
Odtud:
\[x_m = \frac{g}{\left(\frac{2\pi}{T}\right)^2} = \frac{9{,}81 \ \text{m}\cdot \text{s}^{-2}\cdot (0{,}87 \ \text{s})^2}{(2\pi)^2} \dot = 0{,}188 \ \text{m} \dot = 18{,}8 \ \text{cm}.\]

Odpovědi

a)	Pružina se po zavěsení nádoby prodlouží o x₀ \(\dot{=}\) 3,9 cm.
b)	Amplituda, s kterou nádoba s koulí kmitá, je x_A \(\dot{=}\) 14,7 cm.
c)	Doba kmitu nádoby s koulí je T \(\dot{=}\) 0,87 s, maximální zrychlení je a \(\dot{=}\) 7,74 m·s^-2.
e)	V nejnižší poloze působí koule na dno nádoby silou F_m \(\dot{=}\) 26,3 N.
f)	Amplituda, s kterou může nádoba s koulí kmitat tak, aby se koule i ve svojí nejvyšší krajní poloze stále dotýkala nádoby, je x_m \(\dot{=}\) 18,8 cm.