Koule přivázaná na konci provazu
Úloha číslo: 150
Koule o hmotnosti m přivázaná na konci provazu délky L se pohybuje po kružnici ve svislé rovině. V nejvyšším bodě trajektorie je napětí provazu právě nulové. Určete velikost rychlosti koule v místech, kde je provaz vodorovný, a v nejnižším bodě. Jak velkou silou je provaz v těchto místech napínán? Odpor vzduchu a hmotnost provazu neuvažujte.
Poznámka: Místo velikost rychlosti píšeme dále jen rychlost.
Zápis
m hmotnost koule L délka provazu T1 = 0 velikost tahové síly, kterou na kouli působí provaz v nejvyšším bodě trajektorie T2 = ? velikost tahové síly, kterou na kouli působí provaz v okamžiku, kdy je provaz poprvé vodorovně T3 = ? velikost tahové síly, kterou na kouli působí provaz v nejnižším bodě trajektorie T4 = ? velikost tahové síly, kterou na kouli působí provaz v okamžiku, kdy je provaz podruhé vodorovně v1 = ? rychlost koule v nejvyšším bodě trajektorie v2 = ? rychlost koule v okamžiku, kdy je provaz poprvé vodorovně v3 = ? rychlost koule v nejnižším bodě trajektorie v4 = ? rychlost koule v okamžiku, kdy je provaz podruhé vodorovně Rozbor
S využitím 2. Newtonova zákona zjistíme nejprve rychlost koule v nejvyšším bodě. Rychlosti v dalších bodech určíme pomocí zákona zachování mechanické energie. K určení síly, kterou je napínán provaz, pak použijeme 2. Newtonův zákon.
Nápověda 1 - rychlost koule v nejvyšším bodě
Nakreslete si obrázek a vyznačte body, které nás zajímají, přičemž bod 1 značí nejvyšší bod. Zakreslete si všechny síly působící na kouli v nejvyšším bodě a napište pro ni pohybovou rovnici.
Nápověda 2 - rychlost koule v dalších bodech
Při pohybu koule z bodu 1 postupně do bodu 2, 3, 4 se mění jak její potenciální, tak kinetická energie, ale celková mechanická energie se zachovává. Platí tedy zákon zachování mechanické energie (ZZME). Zvolte hladinu nulové potenciální energie. Napište, jaká je celková mechanická energie koule v bodě 1 a v bodě 2, a vyjádřete odtud rychlost v2. Obdobně postupujte pro další body.
Nápověda 3 - síla, kterou je napínán provaz
Nakreslete si do obrázku všechny síly, které působí na kouli v bodech 2, 3 a 4. Napište pohybové rovnice pro kouli v těchto bodech a vyjádřete z nich hledané tahové síly.
Odpověď
V nejvyšším bodě je velikost rychlosti koule rovna \(v_1=\sqrt{gL}\) a síla, kterou je provaz v tomto bodě napínán, je nulová.
V bodech 2 a 4 je velikost rychlosti koule rovna \(v_2=v_4=\sqrt{3gL}\) a velikost síly, kterou je provaz napínán, je rovna \(T_2^{'}=T_4^{'}=3mg\).
V bodě 3 je velikost rychlosti koule rovna \(v_3=\sqrt{5gL}\) a velikost síly, kterou je provaz napínán, je rovna \(T_3^{'}=6mg\).
Celkové řešení
S využitím 2. Newtonova zákona zjistíme nejprve rychlost koule v nejvyšším bodě. Rychlosti v dalších bodech určíme pomocí zákona zachování mechanické energie (ZZME). K určení síly, kterou je napínán provaz, pak použijeme 2. Newtonův zákon.
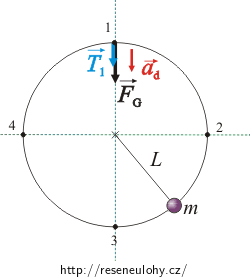
V nejvyšším bodě trajektorie působí na kouli tíhová síla \(\vec{F_\mathrm{G}}\) a tahová síla \(\vec{T_1}\), kterou na kouli působí provaz. Zrychlení koule \(\vec{a_\mathrm{d}}\) směřuje dolů ke středu kružnice.
Pohybová rovnice pro kouli:
\[\vec{T_1}+\vec{F_\mathrm{G}}\,=\,m\vec{a_\mathrm{d}}.\tag{1}\]Obě síly leží v přímce, pohybovou rovnici přepíšeme skalárně:
\[T_1+F_\mathrm{G}\,=\,ma_\mathrm{d},\] \[T_1+mg\,=\,ma_\mathrm{d},\]\(m\)…hmotnost koule,
\(g\)…tíhové zrychlení.
Tahová síla provazu je v nejvyšším bodě nulová, \(T_1\,=\,0\):
\[mg\,=\,ma_\mathrm{d}.\]Normálové zrychlení koule vyjádříme vztahem:
\[a_\mathrm{d} \,=\, \frac{v_1^2}{L},\]\(v_1\)…rychlost koule v nejvyšším bodě,
\(L\)… délka provazu,
\[mg\,=\,m\frac{v_1^2}{L}.\]Odsud si vyjádříme rychlost koule \(v_1\):
\[v_1\,=\,\sqrt{gL}.\tag{2}\]Při pohybu koule z bodu 1 postupně do bodu 2, 3, 4 se mění jak její potenciální, tak kinetická energie, ale celková mechanická energie se zachovává. Platí tedy zákon zachování mechanické energie (ZZME). Zvolíme hladinu nulové potenciální energie. Napíšeme, jaká je celková mechanická energie koule v bodě 1 a v bodě 2, a odtud vyjádříme rychlost v2. Podobně budeme postupovat pro další body.
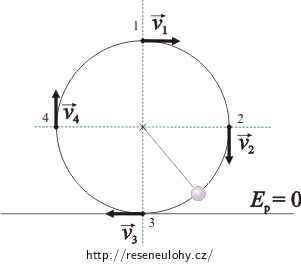
Pohyb koule z bodu 1 do bodu 2:
\[\mathrm{ZZME:} \hspace{15px} E_\mathrm{k1}+E_\mathrm{p1}\,=\,E_\mathrm{k2}+E_\mathrm{p2},\]\(E_\mathrm{k1}\)…kinetická energie koule v bodě 1,
\(E_\mathrm{k2}\)…kinetická energie koule v bodě 2,
\(E_\mathrm{p1}\)…potenciální energie koule v bodě 1,
\(E_\mathrm{p2}\)…potenciální energie koule v bodě 2,
\[\frac{1}{2}mv_1^2+mg2L\,=\,\frac{1}{2}mv_2^2+mgL.\]Ze vztahu (2) dosadíme za rychlost v1:
\[\frac{1}{2}mgL+mg2L\,=\,\frac{1}{2}mv_2^2+mgL.\]Rovnici vydělíme hmotností koule m, vynásobíme dvěma a vyjádříme rychlost v2:
\[gL+4gL\,=\,v_2^2+2gL,\] \[3gL\,=\,v_2^2,\] \[v_2\,=\,\sqrt{3gL}.\tag{3}\]Pohyb koule z bodu 2 do bodu 3:
\[\mathrm{ZZME:} \hspace{15px} E_\mathrm{k2}+E_\mathrm{p2}\,=\,E_\mathrm{k3}+E_\mathrm{p3},\]\(E_\mathrm{k3}\)…kinetická energie koule v bodě 3,
\(E_\mathrm{p3}\)…potenciální energie koule v bodě 3,
V bodě 3 je potenciální energie koule nulová, \(E_\mathrm{p3}\,=\,0:\)
\[E_\mathrm{k2}+E_\mathrm{p2}\,=\,E_\mathrm{k3}+0,\] \[\frac{1}{2}mv_2^2+mgL\,=\,\frac{1}{2}mv_3^2.\]Za rychlost v2 dosadíme ze vztahu (3):
\[\frac{1}{2}m3gL+mgL\,=\,\frac{1}{2}mv_3^2.\]Rovnici vydělíme hmotností koule m, vynásobíme dvěma a vyjádříme rychlost v3:
\[3gL+2gL\,=\,v_3^2,\] \[v_3\,=\,\sqrt{5gL}.\tag{4}\]Pohyb koule z bodu 3 do bodu 4:
\[\mathrm{ZZME:} \hspace{15px} E_\mathrm{k3}+E_\mathrm{p3}\,=\,E_\mathrm{k4}+E_\mathrm{p4},\]\(E_\mathrm{k4}\)…kinetická energie koule v bodě 4,
\(E_\mathrm{p4}\)…potenciální energie koule v bodě 4,
\[E_\mathrm{k3}+0\,=\,E_\mathrm{k4}+E_\mathrm{p4},\] \[\frac{1}{2}mv_3^2\,=\,\frac{1}{2}mv_4^2+mgL.\]Za rychlost v3 dosadíme ze vztahu (4):
\[\frac{1}{2}m5gl\,=\,\frac{1}{2}mv_4^2+mgL.\]Rovnici vydělíme hmotností koule m, vynásobíme dvěma a vyjádříme rychlost v4:
\[5gl\,=\,v_4^2+2gL,\] \[v_4\,=\,\sqrt{3gL}.\tag{5}\]Nakreslíme do obrázku všechny síly, které působí na kouli v bodech 2, 3 a 4. Napíšeme pohybové rovnice pro kouli v těchto bodech a vyjádříme z nich hledané tahové síly.
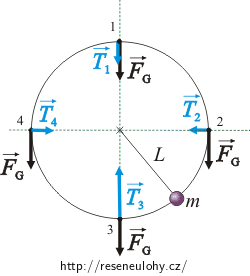
V nejvyšším bodě je podle zadání síla, kterou je napínán provaz, nulová:
\[T_1^{'}\,=\,0.\]Pohybová rovnice pro kouli v bodě 2:
\[\vec{T_2}+\vec{F_\mathrm{G}}\,=\,m\vec{a},\]\(T_2\)…síla, kterou působí provaz na kouli v bodě 2.
Přepíšeme pohybovou rovnici skalárně. Souřadný systém volíme tak, že osa x směřuje ve směru pohybu koule a osa y do středu kružnice (viz obrázek).
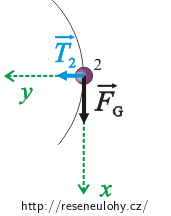
x-ová složka:
\[F_\mathrm{G}\,=\,ma_\mathrm{t},\]\(a_\mathrm{t}\)…tečné zrychlení.
y-ová složka:
\[T_2\,=\,ma_\mathrm{d},\]\(a_d\)…normálové zrychlení.
Velikost normálového zrychlení koule v bodě 2 je rovna:
\[a_\mathrm{d}\,=\,\frac{v_2^2}{L},\] \[T_2\,=\,\frac{mv_2^2}{L}\,=\,\frac{m3gL}{L}\,=\,3mg.\]Tahová síla \(T_2^{'}\), kterou je napínán provaz v bodě 2, je podle 3. Newtonova zákona stejně velká jako síla T2, kterou působí provaz na kouli, ale opačného směru:
\[T_2^{'}\,=\,T_2\,=\,3mg.\]Analogická je situace v bodě 4. Protože je rychlost koule v bodech 2 a 4 stejně velká, je stejně velká i síla T4, kterou na ni působí provaz, a tedy i tahová síla \(T_4^{'}\), kterou je provaz napínán:
\[T_4\,=\,ma_d\,=\,\frac{mv_4^2}{L}\,=\,3mg,\] \[T_4^{'}\,=\,T_4\,=\,3mg.\]Pohybová rovnice pro kouli v bodě 3:
\[\vec{T_3}+\vec{F_\mathrm{G}}\,=\,m\vec{a_\mathrm{d}},\]\(T_3\)…síla, kterou působí provaz na kouli v bodě 3.
Přepíšeme pohybovou rovnici skalárně. Souřadný systém volíme tak, že osa x směřuje ve směru pohybu koule a osa y do středu kružnice (viz obrázek):
\[T_3-F_\mathrm{G}\,=\,ma_\mathrm{d},\] \[T_3-F_\mathrm{G}\,=\,m\frac{v_3^2}{L},\] \[T_3-mg\,=\,m\frac{5gL}{L},\] \[T_3\,=\,mg+5mg,\] \[T_3\,=\,6mg.\]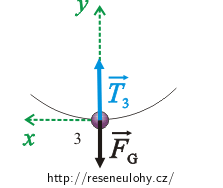
Podle 3. Newtonova zákona opět platí, že síla \(T_3^{'}\), kterou je napínán provaz v bodě 3, je stejně velká jako síla T3, kterou působí provaz na kouli, ale opačného směru:
\[T_3^{'}\,=\,T_3\,=\,6mg.\]Odpověď:
V nejvyšším bodě je velikost rychlosti koule rovna \(v_1\,=\,\sqrt{gL}\) a síla, kterou je provaz v tomto bodě napínán, je nulová.
V bodech 2 a 4 je velikost rychlosti koule rovna \(v_2\,=\,v_4\,=\,\sqrt{3gL}\) a velikost síly, kterou je provaz napínán, je rovna \(T_2^{'}\,=\,T_4^{'}\,=\,3mg\).
V bodě 3 je velikost rychlosti koule rovna \(v_3\,=\,\sqrt{5gL}\) a velikost síly, kterou je provaz napínán, je rovna \(T_3^{'}\,=\,6mg\).



