Cyklista jede po silnici
Úloha číslo: 83
Po vodorovné přímé silnici jede cyklista stálou rychlostí 27 km·h−1. Odporová síla má velikost Fodp = kv2, kde číselná hodnota {k} = 0,3, přičemž rychlost uvádíme v jednotkách m·s−1 a sílu v newtonech. Hmotnost cyklisty i s kolem je 70 kg. Valivý odpor neuvažujte.
a) Jak velkou silou musí do kola strkat silnice, aby jelo rovnoměrným pohybem?
b) Jakou práci musí cyklista vykonat na trase 1 200 m? Jaký je výkon cyklisty při jízdě? Předpokládejte, že nedochází ke ztrátám mechanické energie.
c) Jakou největší rychlost může vyvinout cyklista při stálem výkonu 600 W?
Zápis
v = 27 km·h−1 rychlost cyklisty Fodp = kv2 odporová síla {k} = 0,3 konstanta m = 70 kg hmotnost cyklisty s kolem F = ? síla, kterou musíme do kola strkat, aby se pohybovalo rovnoměrně W = ? práce, kterou vykoná cyklista na trase 1200 m P = ? výkon cyklisty při jízdě v = ? největší rychlost, kterou může vyvinout cyklista při stálem výkonu 600 W Nápověda a) – síla, kterou strká silnice
Nakreslete si obrázek jedoucího cyklisty a vyznačte do něj působící síly.
Co můžete říct o výsledné síle, která musí působit na kolo s cyklistou, jede-li stálou rychlostí?
Nápověda b1) – práce cyklisty
Předpokládáme-li, že nedochází ke ztrátám mechanické energie, je práce vykonaná cyklistou rovna práci, kterou vykoná síla, kterou strká silnice do kola, na dané dráze.
Nápověda b2) – výkon cyklisty
Jak můžeme spočítat výkon, známe-li sílu a rychlost, jakou se cyklista pohybuje?
Nápověda c) – maximalní rychlost při daném výkonu
Nyní je daný výkon a potřebujeme zjistit rychlost.
Nezapomeňte, že síla, kterou působí silnice na kolo, se rovná odporové síle. Platí pro ni vztah:
\[F\,=\,kv^{2}\,.\tag{2}\]Číselný výpočet
a)
Dáno:
k = 0,3 kg·m−1
v = 27 km·h−1 = 7,5 m·s−1
Hledáme:
F = ?
\[F\,=\,kv^{2}\,=\,0{,}3{\cdot}7{,}5^{2}\,\mathrm{N}\] \[F\,=\,16{,}9\, \mathrm{N}\]b)
Dáno:
F = 16,9 N
s = 1 200 m
v = 7,5 m·s−1
Hledáme:
W = ?
P = ?
\[W\,=\,Fs\,=\,16{,}9\,\cdot\,1\,200\,\mathrm{J}\] \[W\,=\,20\,280\, \mathrm{J}\,\,\dot=\,20{,}3\ \mathrm{kJ}\] \[P\,=\,Fv\,=\,16{,}9{\cdot}7{,}5\,\mathrm{W}\] \[P\,=\,127\, \mathrm{W}\]c)
Dáno:
P = 600 W
k = 0,3 kg·m−1
Hledáme:
v = ?
\[v=\sqrt[3]{\frac{P}{k}}\,=\,\sqrt[3]{\frac{600}{0{,}3}}\,\mathrm{m \cdot s^{-1}}\] \[v\,=\,12{,}6\, \mathrm{m \cdot s^{-1}}\,=\,45{,}4\, \mathrm{km \cdot h^{-1}}\]Odpověď
a) Síla, kterou silnice strká do kola, je rovna \(F\,=\,kv^2\,=\,16{,}9\,\mathrm{N}\).
b) Na trase 1 200 m musí cyklista vykonat práci rovnou \(W\,=\,Fs\,\,\dot=\,20{,}3\ \mathrm{kJ}\,.\) Výkon cyklisty při jízdě je \(P\,=\,Fv\,=\,127\,\mathrm{W}\).
c) Maximální rychlost, kterou může cyklista vyvinout při stálem výkonu 600 W, je\(v\,=\,\sqrt[3]{\frac{P}{k}}\,=\,45{,}4\, \mathrm{km \cdot h^{-1}}\).
Poznámka: Co by se změnilo, kdyby...
Zkusme ještě spočítat, co a jak by se změnilo, kdyby byla rychlost cyklisty 18 km·h−1 nebo 45 km·h−1.
Pro rychlost cyklisty 18 km·h−1:
a)
k = 0,3 kg·m−1
v = 18 km·h−1 = 5 m·s−1
F = ?
\[F\,=\,kv^2\,=\,0{,}3{\cdot} 5^2\,\mathrm{N}\] \[F\,=\,7{,}5 \,\mathrm{N}\]b)
F = 7,5 N
s = 1 200 m
v =¯5 m·s−1
\[W\,=\,Fs\,=\,7{,}5 \cdot\, 1\,200\,\mathrm{J}\] \[W\,=\,9\,000\, \mathrm{J}\,=\,9\, \mathrm{kJ}\] \[P\,=\,Fv\,=\,7{,}5{\cdot} 5\,\mathrm{W}\] \[P\,=\,37{,}5\, \mathrm{W}\]c)
P = 600 W
k = 0,3
\[v\,=\,\sqrt[3]{\frac{P}{k}}\,=\,\sqrt[3]{\frac {600}{0{,}3}}\,\mathrm{m \cdot s^{-1}}\] \[v\,=\,12{,}5\,\mathrm{m \cdot s^{-1}}\]Při menší rychlosti cyklisty se zmenší odporová síla, a tím pádem i síla, kterou silnice strká do kola. Menší bude i práce, kterou cyklista vykonal, i jeho výkon. Pro bod c) zůstal výsledek stejný.
Pro rychlost cyklisty 45 km·h−1:
a)
k = 0,3 kg·m−1
v = 45 km·h−1 = 12,5 m·s−1
F = ?
\[F\,=\,kv^2\,=\,0{,}3{\cdot} 12{,}5^2\,\mathrm{N}\] \[F\,=\,46{,}9 \,\mathrm{N}\]b)
F = 46,9 N
s = 1 200 m
v = 12,5 m·s−1
\[W\,=\,Fs\,=\,46{,}9 \cdot \,1\,200\,\mathrm{J}\] \[W\,=\,56\,280\, \mathrm{J}\,\,\dot=\,56{,}3\ \mathrm{kJ}\] \[P\,=\,Fv\,=\,46{,}9{\cdot} 12{,}5\,\mathrm{W}\] \[P\,=\,586\, \mathrm{W}\]c)
P = 600 W
k = 0,3
\[v\,=\,\sqrt[3]{\frac{P}{k}}\,=\,\sqrt[3]{\frac {600}{0{,}3}}\,\mathrm{m \cdot s^{-1}}\] \[v\,=\,12{,}5\,\mathrm{m \cdot s^{-1}}\]Při větší rychlosti cyklisty se zvětší odporová síla a tím pádem i síla, kterou silnice strká do kola. Větší bude i práce, kterou cyklista vykonal, i jeho výkon. Pro bod c) zůstal výsledek stejný.
Celkové řešení bodu a)

Pro zjednodušení si představíme cyklistu s kolem jako jedno těleso. Zakreslíme si do obrázku všechny působící síly.
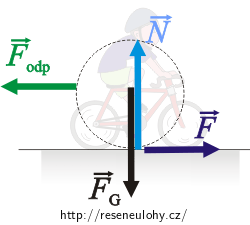
\(\vec{F}\)…hledaná síla, kterou do kola strká silnice
\(\vec{N}\)…síla, kterou do kola tlačí silnice
\(\vec{F}_\mathrm{g}\)…tíhová síla
\(\vec{F}_\mathrm{odp}\)…odporová síla
Výsledná síla působící na cyklistu s kolem musí být při rovnoměrném přímočarém pohybu rovna nule:
\[\vec{F}_\mathrm{g}\,\,+\,\,\vec{N}\,\,+\,\,\vec{F}_\mathrm{odp}\,\,+\,\,\vec{F}\,=\,O.\]Tíhová síla, kterou na cyklistu s kolem působí Země, se vyruší se silou, kterou do kola tlačí silnice:
\[F_\mathrm{g}-N\,=\,0.\]Síla, kterou do kola strká silnice, musí být rovna odporové síle:
\[F\,=\,F_\mathrm{odp}\,=\,kv^{2},\] \[F\,=\,0{,}3{\cdot}7{,}5^{2}\,\mathrm{N},\] \[F\,=\,16{,}9\, \mathrm{N}.\]k…konstanta
v…rychlost cyklisty
Odpověď: Síla, kterou silnice strká do kola, je F = 16,9 N.
Celkové řešení bodu b)
Síla, kterou strká do kola silnice, je konstantní a působí ve směru posunutí cyklisty, takže práci spočítáme podle vztahu:
\[W\,=\,Fs\,=\,kv^2s,\] \[W\,=\,16{,}9\cdot\,1\,200\,\mathrm{J},\] \[W\,=\,20\,280\, \mathrm{J}\,\dot=20{,}3\ \mathrm{kJ}.\]W…vykonaná práce
F…síla, kterou strká silnice do kola
s…ujetá dráha
v…rychlost cyklisty
Pro okamžitý výkon platí:
\[P\,=\,\frac{dW}{dt}\,=\,\frac {\mathrm{d}F\cdot s}{\mathrm{d}t}\,=\,F\cdot\frac {\mathrm{d}s}{\mathrm{d}t}\,=\,F\cdot v.\tag{1}\] \[P\,=\,Fv,\] \[P\,=\,16{,}9{\cdot}7{,}5\,\mathrm{W},\] \[P\,=\,127\, \mathrm{W}.\]Odpověď:
Na trase 1 200 m musí cyklista vykonat práci rovnou \(W\,\dot=\,20{,}3\ \mathrm{kJ}.\)
Výkon cyklisty při jízdě je \(P\,=\,127\,\mathrm{W}.\)
Celkové řešení bodu c)
Do vztahu pro okamžitý výkon \(P=Fv\) dosadíme za sílu F:
\[F\,=\,kv^{2},\] \[P\,=\,kv^{3}.\]Odtud vyjádříme rychlost:
\[v^{3}\,=\,\frac{P}{k}.\]Rovnici odmocníme:
\[v\,=\,\sqrt[3]{\frac{P}{k}},\] \[v\,=\,\sqrt[3]{\frac{600}{0{,}3}}\,\mathrm{m \cdot s^{-1}},\] \[v\,=\,12{,}6\,\mathrm{m \cdot s^{-1}}\,=\,45{,}4\, \mathrm{km \cdot h^{-1}}.\]Odpověď: Maximální rychlost, kterou může cyklista vyvinout při stálem výkonu 600 W, je\(v=45{,}4\, \mathrm{km \cdot h^{-1}}\).




