Punker na desce
Úloha číslo: 531
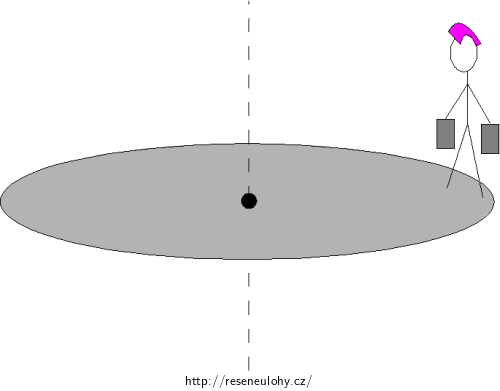
Na obvodu nehybné vodorovné homogenní kruhové desky o hmotnosti 140 kg a poloměru 4 m, volně otáčivé kolem svislé osy ve středu, stojí punker o hmotnosti 79 kg se dvěma kilogramovými závažími v rukou.
a) S jakou úhlovou rychlostí se začne deska otáčet, odhodí-li punker jedno závaží ve směru tečném k obvodu desky s počáteční rychlostí 20 m·s-1?
b) Jaká bude úhlová rychlost desky, přejde-li punker poté o 2 m blíž k ose?
c) Jaká bude úhlová rychlost desky, odhodí-li punker druhé závaží podobně jako to první, rychlostí 20 m·s-1 vzhledem k rotující desce?
Zápis
M = 140 kg hmotnost desky r = 4 m poloměr desky m1 = 79 kg hmotnost punkera m0 = 1 kg hmotnost závaží v0 = 20 m·s-1 počáteční rychlost závaží ω1 = ? (s−1) úhlová rychlost otáčení desky po odhození prvního závaží ω2 = ? (s−1) úhlová rychlost otáčení desky, přejde-li punker po odhození prvního závaží o 2 m blíž k ose ω3 = ? (s−1) úhlová rychlost otáčení desky po odhození druhého závaží Momenty setrvačnosti:
Podle tabulek je moment setrvačnosti desky (i válce) o hmotnosti M a poloměru r při otáčení podle osy symetrie \(J=\frac{1}{2}Mr^2\).
Těleso, jehož veškerá hmotnost m je ve vzdálenosti r od osy otáčení, má moment setrvačnosti \(J=mr^2\).
Nápověda 1
K řešení úlohy využijeme zákon zachování momentu hybnosti. Uvědomte si, jak je definován moment hybnosti. Zapište jeho definici pro hmotný bod a také vztah, který můžete použít v případě tuhého tělesa otáčejícího se okolo pevné osy.
Zapište i příslušné velikosti vektoru momentu hybnosti a uvědomte si, kam vektor míří.
Nápověda 2a)
Zapište, čemu je roven moment hybnosti soustavy deska–punker–obě závaží před odhozením prvního závaží a těsně po jeho odhození. Zjistěte směry momentů hybnosti a napište i jejich velikosti.
Nápověda 3a)
K vyjádření hledané úhlové rychlosti využijte zákon zachování momentu hybnosti.
Nápověda 4b)
Zapište, čemu je roven moment hybnosti soustavy deska–punker–zbylé závaží před přesunem punkera a po přesunu. Zjistěte směry momentů hybnosti a napište i jejich velikosti.
Nápověda 5b)
K vyjádření hledané úhlové rychlosti využijte opět zákon zachování momentu hybnosti.
Nápověda 6c):
Zapište, čemu je roven moment hybnosti soustavy deska-punker-zbylé závaží před odhozením závaží a po něm. Zjistěte směry momentů hybnosti a napište i jejich velikosti.
Nápověda 7c)
Zřejmě už nikoho nepřekvapí, že k hledání úhlové rychlosti je třeba použít zákon zachování momentu hybnosti.
Celkové řešení
Zápis:
M = 140 kg...hmotnost desky
r = 4 m...poloměr desky
m1 = 79 kg...hmotnost punkera
m0 = 1 kg...hmotnost závaží
v0 = 20 ms-1...počáteční rychlost závaží
K řešení úlohy využijeme zákon zachování momentu hybnosti.
Potřebné vztahy:
Podle tabulek je moment setrvačnosti desky (i válce) o hmotnosti m a poloměru r při otáčení podle osy symetrie \(J=\frac{1}{2}mr^2\).
Těleso, jehož veškerá hmotnost m je ve vzdálenosti r od osy otáčení, má moment setrvačnosti \(J=mr^2\).
Moment hybnosti \(\vec{L}\) hmotného bodu vzhledem k bodu S je definován jako vektorový součin polohového vektoru \(\vec{r}\) a hybnosti \(\vec{p}\) hmotného bodu:
\[\vec{L}=\vec{r}\times\vec{p}\,.\]Pro velikost vektorového součinu platí:
\[L=rp\sin\varphi\,,\] kde φ je úhel sevřený oběma vektory.Směr momentu hybnosti je kolmý na rovinu, ve které leží vektory \(\vec{r}\) a \(\vec{p}\), orientace se určí pomocí pravidla pravé ruky: prsty dáme tak, aby směřovaly od \(\vec{r}\) k \(\vec{p}\), napnutý palec pak ukazuje směr vektoru \(\vec{L}\).
Pro moment hybnosti tuhého tělesa vzhledem k pevné ose otáčení platí:
\[\vec{L} = J\vec{\omega}\,,\]kde J je moment setrvačnosti tělesa vzhledem k pevné ose otáčení a \(\vec{\omega}\) úhlová rychlost otáčení.
(Orientace \(\vec{\omega}\) odpovídá \(\vec{L}\), dá se zjistit pravidlem pravé ruky: přiložíme prsty ve směru otáčení a palec ukazuje orientaci \(\vec{\omega}\))
Skalárně
\[L=J\omega\,,\]kde J je moment setrvačnosti tělesa vzhledem k pevné ose otáčení a ω úhlová rychlost otáčení.
a) odhození prvního závaží
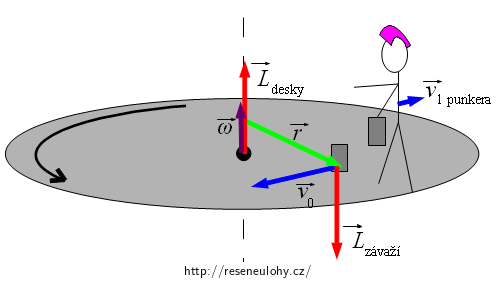
Celkový moment hybnosti před odhozením závaží je moment hybnosti desky, punkera a dvou závaží, vše je vzhledem k okolí v klidu:
\[\vec{L_1}=J_0\vec{\omega}_\mathrm{k}+\vec{r}\times (m_1\vec{v}_\mathrm{k})+2[\vec{r}\times(m_0\vec{v}_\mathrm{k})],\]kde \(\vec{v}_\mathrm{k}\) je vektor rychlosti předmětů v klidu, tedy nulový vektor. Stejně i \(\vec{\omega}_\mathrm{k}\) je nula:
\[\vec{v}_\mathrm{k}=0\,,\] \[\vec{\omega}_\mathrm{k}=0\,.\] J0 je moment setrvačnosti desky: \[J_0=\frac{1}{2} Mr^2.\] Protože nedochází k žádnému pohybu, je \(\vec{L}_1 = 0.\)Po odhození závaží se celá situace změní:
\[\vec{L_2}=J_0\vec{\omega}_1+\vec{r}\times(m_1\vec{v}_1)+ \vec{r}\times(m_0\vec{v}_1)+\vec{r}\times(m_0\vec{v}_0)\,.\]Jednotlivé členy popisují postupně: desku, punkera, neodhozené závaží, odhozené závaží.
Všimněme si, že vektory \(\vec{v}_0\) (rychlost odhozeného závaží vzhledem k okolí) a \(\vec{v}_1\) (rychlost, kterou se dá do pohybu punker s druhým závažím) mají opačný směr. Příslušné momenty hybnosti budou tedy také mířit na opačné strany. Uvažujme směr momentu hybnosti otáčející se desky jako kladný (v našem případě je to tedy směr nahoru). Přepíšeme skalárně (\(\vec{r}\) je kolmý na \(\vec{v}_1 \) i \(\vec{v}_0)\):
\[L_2=J_0\omega_1+r(m_1v_1)+r(m_0v_1)-r(m_0v_0)\,.\]Ze zákona zachování momentu hybnosti dostáváme:
\[\vec{L}_1=\vec{L}_2\,.\]Rovnost platí i pro velikosti momentů hybnosti:
\[L_1=L_2\,,\] \[0 = J_0\omega_1+r(m_1v_1)+r(m_0v_1)-r(m_0v_0).\]Pro úhlovou rychlost desky a obvodovou rychlost punkera platí \[v_1=r\omega_1\,.\]
Dosadíme:
\[0 = J_0\omega_1+r(m_1r\omega_1)+r(m_0r\omega_1)-r(m_0v_0)\,.\]Vyjádříme úhlovou rychlost:
\[0 = \omega_1(J_0+r(m_1r)+r(m_0r))-r(m_0v_0)\,,\] \[\omega_1(J_0+r(m_1r)+r(m_0r))=r(m_0v_0)\,,\] \[\omega_1=\frac{rm_0v_0}{J_0+r(m_1r)+r(m_0r)}\,,\]Ještě dosadíme za J0:
\[\omega_1=\frac{rm_0v_0}{ \frac{1}{2}Mr^2+r(m_1r)+r(m_0r)}\,,\]r se pokrátí:
\[\omega_1=\frac{m_0v_0}{r(\frac{M}{2}+m_1+m_0)}\,.\]Dosadíme-li známé hodnoty, získáváme:
\[\omega_1=\frac{1{\cdot}20}{4(\frac{140}{2}+79+1)}\,\mathrm{s^{- 1}}= \frac{1}{30}\,\mathrm{s^{-1}}\dot{=}0{,}03 \,\mathrm{s^{- 1}}\,.\]b) přechod do poloviční vzdálenosti
Moment hybnosti L3 naší nové soustavy před přesunem dovedeme napsat s využitím informací, které jsme získali při řešení problému a):
\[\vec{L}_3= J_0\vec{\omega}_1+\vec{r}\times(m_1\vec{v}_1)+\vec{r}\times(m_0\vec{v}_1)\,.\]Porovnáme-li s L2:
\[\vec{L}_2=J_0\vec{\omega}_1+\vec{r}\times(m_1\vec{v}_1)+\vec{r}\times(m_0\vec{v}_1)+\vec{r}\times(m_0\vec{v}_0)\,.\]A víme-li z Řešení nápovědy 3a):
\[L_2=0\,.\]Pak:
\[\vec{L}_3+ \vec{r}\times(m_0\vec{v}_0)=\vec{0}\,,\] \[\vec{L}_3= -\vec{r}\times(m_0\vec{v}_0)\,,\]což můžeme přepsat skalárně:
\[L_3 = r(m_0v_0)\,.\](Moment hybnosti odhozeného závaží jsme brali jako záporný.)
Situace po přechodu punkera do vzdálenosti \(\frac{r}{2}\) od středu se změní následovně:
\[\vec{L}_4= J_0\vec{\omega}_2+\frac{\vec{r}}{2}\times(m_1\vec{v}_2)+\frac{\vec{r}}{2}\times(m_0\vec{v}_2)\,,\](kde \(\omega_2\) je úhlová rychlost desky po přechodu punkera)
což je přepsáno skalárně:
\[L_4= J_0\omega_2+\frac{r}{2}m_1v_2+\frac{r}{2}(m_0v_2)\,.\]Ze zákona zachování momentu hybnosti dostáváme
\[\vec{L}_3=\vec{L}_4\,.\]Rovnost platí i pro velikosti momentů hybnosti:
\[L_3=L_4\,.\]Dosadíme:
\[rm_0v_0= J_0\omega_2+\frac{r}{2}m_1v_2+\frac{r}{2}m_0v_2\,.\]Punker stojí ve vzdálenosti \(\frac{r}{2}\), pro obvodovou rychlost tedy platí:
\[v_2 =\frac{r}{2}\omega_2\,,\] \[rm_0v_0= J_0\omega_2+\frac{r}{2}m_1\frac{r}{2}\omega_2+\frac{r}{2}m_0\frac{r}{2}\omega_2\,.\]Obdobně jako v a) vyjádříme ω2:
\[rm_0v_0= \omega_2(J_0+\frac{r}{2}m_1\frac{r}{2}+\frac{r}{2}m_0\frac{r}{2})\,,\] \[\omega_2= \frac{rm_0v_0}{J_0+\frac{r}{2}m_1\frac{r}{2}+\frac{r}{2}m_0\frac{r}{2}}\,.\]Dosadíme za J0:
\[\omega_2= \frac{rm_0v_0}{\frac{1}{2}Mr^2+\frac{r}{2}m_1\frac{r}{2}+\frac{r}{2}m_0\frac{r}{2}}\,.\]Vydělíme R:
\[\omega_2= \frac{m_0v_0}{r(\frac{1}{2}M+\frac{1}{2}m_1\frac{1}{2}+\frac{1}{2}m_0\frac{1}{2})}\,,\] \[\omega_2= \frac{2m_0v_0}{r(M+m_1\frac{1}{2}+m_0\frac{1}{2})}\,,\] \[\omega_2= \frac{4m_0v_0}{r(2M+m_1+m_0)}\,.\]Dosadíme-li známé hodnoty, získáváme:
\[\omega_2= \frac{4{\cdot} 1\cdot 20}{4(2{\cdot} 140+79+1)}\,\mathrm{s^{-1}} = \frac{1}{18}\,\mathrm{s^{-1}}\dot{=}0{,}06 \,\mathrm{s^{-1}}\,.\]c) odhození druhého závaží
V tomto případě máme usnadněnou práci, protože se nijak nezměnila naše soustava od okamžiku, kdy punker přešel blíže ke středu. Moment hybnosti L5 je:
\[\vec{L}_5=\vec{L}_4\,.\]Dále z řešení nápovědy 5b) víme:
\[\vec{L}_5=\vec{L}_3\,.\]A o \(\vec{L}_3\) víme:
\[\vec{L}_3 = -\vec{r}\times(m_0\vec{v}_0)\,.\]Tedy:
\[\vec{L}_5 = -\vec{r}\times(m_0\vec{v}_0)\,.\]Skalárně:
\[L_5 = rm_0v_0\,.\]Situace po odhození závaží si zaslouží opět rozepsat:
\[\vec{L}_6= J_0\omega_3+\frac{\vec{r}}{2}\times(m_1\vec{v}_3)+\frac{\vec{r}}{2}\times(m_0(\vec{v}_0+\vec{v}_\mathrm{ot}))\,,\]kde \(\omega_3\) je úhlová rychlost desky po odhození druhéhé závaží.
Všimněme si, že rychlost odhozeného závaží se skládá z \(\vec{v}_\mathrm{ot}\). To je způsobeno tím, že punker odhodí závaží od sebe rychlostí \(\vec{v}_0\), sám se však pohybuje opačným směrem. Celková rychlost závaží vůči nehybnému pozorovateli je tak složením těchto dvou rychlostí. Z tohoto důvodu se skalárně budou rychlosti odčítat.
Moment hybnosti odhozeného závaží má opačný směr než otáčející se desky, budeme ho opět brát jako záporný, proto skalárně:
\[L_6= J_0\omega_3+\frac{r}{2}m_1v_3-\frac{r}{2}m_0(v_0-v_\mathrm{ot})\,.\]vot získáme snadno z ω2:
\[v_\mathrm{ot} = \frac{r}{2}\omega_2 = \frac{r}{2} \frac{4(m_0v_0)}{r(2M+m_1+m_0)} =\frac{2(m_0v_0)}{2M+m_1+m_0}\,.\]Ze zákona zachování momentu hybnosti:
\[\vec{L}_5=\vec{L}_6\,.\]Rovnost platí i pro velikosti momentů hybnosti:
\[L_5=L_6\,,\] \[rm_0v_0 = J_0\omega_3+\frac{r}{2}m_1v_3-\frac{r}{2}m_0 (v_0-v_\mathrm{ot})\,.\]Pro obvodovou rychlost punkera platí \(v_3 = \frac{r}{2}\omega_3\):
\[rm_0v_0 = J_0\omega_3+\frac{r}{2}m_1(\frac{r}{2}\omega_3)-\frac{r}{2}m_0(v_0-v_\mathrm{ot})\,,\] \[rm_0v_0+\frac{r}{2}(m_0 (v_0-v_\mathrm{ot})) = J_0\omega_3+\frac{r}{2}(m_1\frac{r}{2}\omega_3)\,.\]Dosadíme vot:
\[rm_0v_0+\frac{r}{2}(m_0 (v_0-\frac{2m_0v_0}{(2M+m_1+m_0)})) = J_0\omega_3+\frac{r}{2}(m_1\frac{r}{2}\omega_3) \,.\]A upravíme:
\[\frac{r}{2}m_0v_0(2+(1-\frac{2m_0}{2M+m_1+m_0}) = J_0\omega_3+\frac{r}{2}(m_1\frac{r}{2}\omega_3) \,,\] \[\frac{r}{2}m_0v_0(3-\frac{2m_0}{2M+m_1+m_0}) = J_0\omega_3+\frac{r}{2}(m_1\frac{r}{2}\omega_3)\,,\] \[\frac{r}{2}m_0v_0\frac{3(2M+m_1+m_0)-2m_0}{2M+m_1+m_0} = J_0\omega_3+\frac{r}{2}(m1\frac{r}{2}\omega_3)\,,\] \[\frac{r}{2}m_0v_0\frac{6M+3m_1+3m_0-2m_0}{2M+m_1+m_0} = J_0\omega_3+\frac{r}{2}(m_1\frac{r}{2}\omega_3)\,,\] \[\frac{r}{2}m_0v_0\frac{6M+3m_1+m_0}{2M+m_1+m_0} = J_0\omega_3+\frac{r}{2}(m_1\frac{r}{2}\omega_3)\,.\]Dosadíme za J0:
\[\frac{r}{2}m_0v_0\frac{6M+3m_1+m_0}{2M+m_1+m_0} = \frac{1}{2}Mr^2\omega_3+\frac{r}{2}(m_1\frac{r}{2}\omega_3)\,.\]Pokrátíme \(\frac{r}{2}\):
\[\frac{(m_0v_0)(6M+3m_1+m_0)}{2M+m_1+m_0}= Mr\omega_3+m_1\frac{r}{2}\omega_3\,.\]Vyjádříme ω3:
\[\frac{(m_0v_0)(6M+3m_1+m_0)}{2M+m_1+m_0} = \omega_3 (Mr+m_1\frac{r}{2})\,,\] \[\omega_3 = \frac{(m_0v_0) (6M+3m-1+m_0)}{r(M+\frac{m_1}{2}) (2M+m_1+m_0)}\,.\]Číselně:
\[\omega_3= \frac{(1 {\cdot} 20) (6{\cdot} 140+3{\cdot} 79-1+1)}{4(140+\frac{79}{2}) (2{\cdot} 140+79+1)}\,\mathrm{s^{-1}}= \frac{539}{6462}\,\mathrm{s^{-1}}\dot{=}0{,}08 \,\mathrm{s^{-1}}\,.\]Odpověď
Úhlová rychlost desky po odhození prvního závaží je:
\[\omega_1=\frac{m_0v_0}{r(\frac{M}{2}+m_1+m_0)}\,.\]Číselně:
\[\omega_1\dot{=}0{,}03 \,\mathrm{s^{- 1}}\,.\]Úhlová rychlost desky po přesunu punkera je:
\[\omega_2= \frac{4m_0v_0}{r(2M+m_1+m_0)}\,.\]Číselně:
\[\omega_2\dot{=}0{,}06 \,\mathrm{s^{- 1}}\,.\]Úhlová rychlost desky po odhození druhého závaží je:
\[\omega_3 = \frac{(m_0v_0) (6M+3m-1+m_0)}{r(M+\frac{m_1}{2}) (2M+m_1+m_0)}\,.\]Číselně:
\[\omega_3\dot{=}0{,}08 \,\mathrm{s^{- 1}}\,.\]


