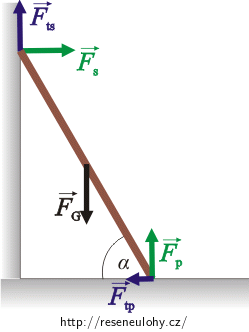
Opřený žebřík
Úloha číslo: 523
Zápis
f1 = 0,3 koeficient statického tření žebříku o stěnu f2 = 0,4 koeficient statického tření žebříku o podlahu α = ?(°) nejmenší možný úhel, jaký může svírat žebřík s podlahou, aby neklouzal Koeficient statického tření
Možná znáte koeficient statického tření jako součinitel klidového tření. Obojí znamená to samé, záleží jen, jestli upřednostňujete cizí slova, nebo jejich české ekvivalenty.
Nápověda 1
Jaké síly na žebřík působí? Zakreslete je do obrázku.Nápověda 2
Co vyplývá pro síly působící na žebřík z faktu, že je v klidu a nepadá?Nápověda 3
Zapište podmínky rovnováhy a přepište je skalárně.Nápověda 4
Uvědomte si, co bude platit pro velikosti klidových třecích sil Ftp a Fts, máme-li stanovit nejmenší úhel, při kterém žebřík ještě nespadne.Nápověda 5
Dosaďte vztahy pro třecí síly do rovnic (1), (2) a (3) a vyjádřete z nich hledaný úhel α.Celkové řešení
Nakreslíme obrázek, vyznačíme působící síly a zvolíme soustavu souřadnic.
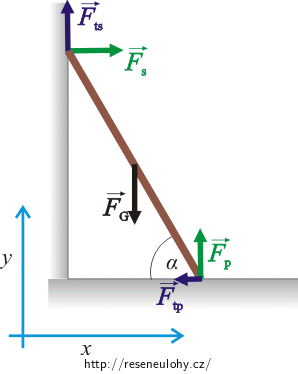
Působící síly udržují žebřík v rovnováze. Znamená to, že výslednice sil působících na žebřík musí být nulová a také výslednice momentů těchto sil musí být rovna nule (vzhledem k libovolnému bodu).
Výslednice sil je nulová: \[\vec{F}_\mathrm{0}G + \vec{F}_\mathrm{p} + \vec{F}_\mathrm{s} + \vec{F}_\mathrm{tp}+ \vec{F}_\mathrm{ts} = \vec{0}\,.\]
Zvolíme soustavu souřadnic podle obrázku a přepíšeme skalárně:
\[x:\hspace{50px}F_\mathrm{s}-F_\mathrm{tp}=0,\tag{1}\] \[y:\hspace{10px}F_\mathrm{p}+ F_\mathrm{ts} - F_\mathrm{G} =0.\tag{2}\]Výslednice momentů sil je vzhledem k libovolnému bodu nulová:
\[\vec{M}_\mathrm{g}+\vec{M}_\mathrm{p}+\vec{M}_\mathrm{s}+\vec{M}_\mathrm{tp}+\vec{M}_\mathrm{ts}=\vec{0}\,.\]Momenty sil budeme určovat například vůči těžišti. Z toho plyne \(\vec{M}_\mathrm{g}=\vec{0}.\)
Připomeňme si ještě vztah pro moment síly \(\vec{F}\) vzhledem k bodu O:
\[\vec{M} = \vec{r} \times \vec{F}\,.\]Pro velikost momentu platí: \(M = rF\sin \varphi\), kde \(\varphi\) je úhel, který svírají vektory \(\vec{r}\) a \(\vec{F}\).
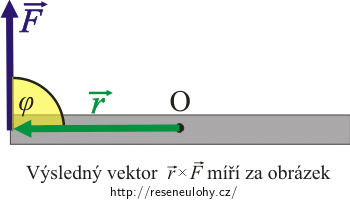
Směr momentu síly je kolmý na rovinu, ve které leží vektory \(\vec{r}\) a \(\vec{F}\), orientace se určí pomocí pravidla pravé ruky: prsty této ruky dáme tak, aby směřovaly od \(\vec{r}\) k \(\vec{F}\), napnutý palec pak ukazuje směr vektoru \(\vec{M}\). Více k vektorovému součinu v úloze Moment síly a vektorový součin.
Za záporný směr otáčení zvolíme směr otáčení hodinových ručiček, momenty sil mířící „za papír“ budeme uvažovat se záporným znaménkem. Pak
\[M_\mathrm{p}-M_\mathrm{s}-M_\mathrm{tp}-M_\mathrm{ts}=0\,.\]Pro velikosti momentů platí:
\[ \frac{L}{2}F_\mathrm{p}\sin(90^{\circ}-\alpha)-\frac{L}{2}F_\mathrm{tp}\sin\alpha - \frac{L}{2}F_\mathrm{s} \sin \alpha- \frac{L}{2}F_\mathrm{ts}\sin(90^{\circ}-\alpha)=0\,.\]Vydělíme L/2 a upravíme:
\[ F_\mathrm{s} \sin \alpha + F_\mathrm{tp}\sin\alpha +F_\mathrm{ts}\cos\alpha=F_\mathrm{p}\cos\alpha\,.\tag{3}\]Při mezním úhlu α platí, že klidová třecí síla dosáhne své maximální hodnoty.
\[F_\mathrm{tp}=F_\mathrm{p} f_2\,,\tag{4}\] \[F_\mathrm{ts}=F_\mathrm{s} f_1\,.\tag{5}\] Dosadíme a vyjádříme.Z (1):
\[F_\mathrm{tp}=F_\mathrm{s}\,.\]Dosadíme do (3):
\[F_\mathrm{s} \sin \alpha + F_\mathrm{ts} \cos \alpha + F_\mathrm{s} \sin \alpha = F_\mathrm{p} \cos \alpha\,.\tag{6}\]Podle (4) a (5):
\[F_\mathrm{s}=F_\mathrm{p} f_2\,,\] \[F_\mathrm{ts}=F_\mathrm{s} f_1 = F_\mathrm{p} f_1 f_2\,.\]Dosadíme do (6):
\[F_\mathrm{p} f_2\sin\alpha+F_\mathrm{p} f_1 f_2 \cos\alpha+F_\mathrm{p} f_2\sin\alpha=F_\mathrm{p}\cos\alpha \,.\]Velikost Fp rozhodně není rovna nule, takže ji můžeme krátit:
\[f_2\sin\alpha+f_1 f_2\cos\alpha+f_2\sin\alpha=\cos\alpha\,.\]Sečteme členy u sinů a cosinů:
\[2f_2\sin\alpha=(1-f_1 f_2)\cos\alpha\,.\]Rovnici upravíme, aby na jedné straně byly členy s α, na druhé zbytek. Vydělíme obě strany 2f2 cosα:
\[\frac{\sin\alpha}{\cos\alpha}=\frac{1-f_1 f_2}{2f_2}.\]Dostáváme výsledek:
\[\mathrm{tg}\alpha=\frac{1-f_1 f_2}{2f_2}\,.\]Dosadíme číselně:
\[\mathrm{tg}\alpha=\frac{1- 0{,}4{\cdot}0{,}3}{2{\cdot}0{,}4} = 1{,}1,\] \[\alpha \dot= 48^{\circ}\,.\]Odpověď
Pro hledaný úhel platí:
\[\mathrm{tg}\alpha=\frac{1-f_2 f_1}{2f_2}\,.\]Číselně:
\[\alpha \dot= 48^{\circ}\,.\]Podobná úloha
Vyřešeno? Vyzkoušejte si i podobnou úlohu Tyč opřená o schod.