Čtyři kostky se třemi pružinami
Úloha číslo: 140
Čtyři stejné dřevěné kostky o hmotnostech m jsou navzájem spojeny za sebou třemi stejnými pružinami o tuhosti k. Kolmo na stěnu krajní kostky tlačíme silou \(\vec{F}\), a tak vyvoláváme rovnoměrně zrychlený pohyb kostek se zrychlením o velikosti a. Určete velikost této síly F a zkrácení každé pružiny, jestliže f je koeficient smykového tření mezi kostkami a vodorovnou podložkou. Hmotnost pružin neuvažujte.

Zápis
m1 hmotnost první kostky m2 hmotnost druhé kostky m3 hmotnost třetí kostky m4 hmotnost čtvrté kostky k tuhost pružin f koeficient smykového tření mezi libovolnou kostkou a podložkou a zrychlení kostek \(\Delta l_1\) = ? zkrácení první pružiny \(\Delta l_2\) = ? zkrácení druhé pružiny \(\Delta l_3\) = ? zkrácení třetí pružiny F = ? velikost působící síly Nápověda 1 - síly působící na kostky
Uvědomte si, jaké síly působí na jednotlivé kostky, a nakreslete je do obrázku.
Nápověda 2 - pohybové rovnice
Napište pro každou kostku pohybovou rovnici. Potom zvolte souřadný systém a přepište pohybové rovnice skalárně.
Nápověda 3 - třecí síla, výpočet síly F
Uvědomte si, na čem závisí velikost třecí síly působící mezi kostkou a podložkou a jak se dá vyjádřit. Z rovnic (6) – (9) pak spočtěte sílu F.
Nápověda 4 - síly stlačující pružiny (zkrácení pružin)
Ze vztahů (7) – (9) vyjádřete velikost sil F1, F2, F3, stlačujících jednotlivé pružiny.
Nápověda 5 - výpočet zkrácení pružin
Síly stlačující pružiny jsou úměrné jejich zkrácení. Vyjádřete tento vztah a spočtěte zkrácení jednotlivých pružin.
CELKOVÉ ŘEŠENÍ
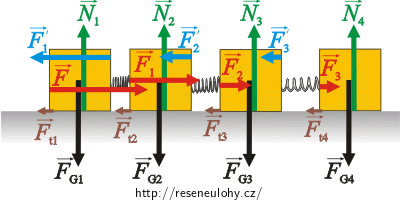
Do obrázku vyznačíme síly působící na jednotlivé kostky a napíšeme pro ně pohybové rovnice.
Síly působící na jednotlivé kostky m1, m2, m3 a m4:
\[\vec{F}_\mathrm{G_1}=\vec{F}_\mathrm{G_2}=\vec{F}_\mathrm{G_3}=\vec{F}_\mathrm{G_4}=\vec{F}_\mathrm{G} \] …síla tíhová působící na jednotlivé kostky m1, m2, m3 a m4 (tíhová síla je pro všechny kostky stejná)
\[\vec{N}_{1}=\vec{N}_{2}=\vec{N}_{3}=\vec{N}_{4}=\vec{N}\] …normálová síla, kterou na jednotlivé kostky m1, m2, m3 a m4 působí podložka (normálová síla je pro všechny kostky stejná)
\[\vec{F}_\mathrm{t_1}=\vec{F}_\mathrm{t_2}=\vec{F}_\mathrm{t_3}=\vec{F}_\mathrm{t_4}=\vec{F}_\mathrm{t}\] …síla třecí mezi každou kostkou m1, m2, m3 a m4 a podložkou (třecí síla je pro všechny kostky stejná)
Na kostky působí dále tyto síly:
Kostka m1:
\(\vec{F}\)…síla, kterou tlačíme kostku,
\(\vec{F}_1\prime\)…síla, kterou působí druhá kostka na první.
Kostka m2:
\(\vec{F}_1\)…síla, kterou působí první kostka na druhou,
\(\vec{F}_2\prime\)…síla, kterou působí třetí kostka na druhou.
Kostka m3:
\(\vec{F}_2\)…síla, kterou působí druhá kostka na třetí,
\(\vec{F}_3\prime\)…síla, kterou působí čtvrtá kostka na třetí.
Kostka m4:
\(\vec{F}_3\)…síla, kterou působí třetí kostka na čtvrtou.
Pohybové rovnice pro jednotlivé kostky:
\[m_1:\qquad\vec{F}+\vec{N}+\vec{F}_\mathrm{G}+\vec{F}_\mathrm{t}+\vec{F}_{1}\prime\,=\,m\vec{a},\] \[m_2:\qquad\vec{F}_1+\vec{N}+\vec{F}_\mathrm{G}+\vec{F}_\mathrm{t}+\vec{F}_{2}\prime\,=\,m\vec{a},\] \[m_3:\qquad\vec{F}_2+\vec{N}+\vec{F}_\mathrm{G}+\vec{F}_\mathrm{t}+\vec{F}_{3}\prime\,=\,m\vec{a},\] \[m_4:\qquad\vec{F}_3+\vec{N}+\vec{F}_\mathrm{G}+\vec{F}_\mathrm{t}\,=\,m\vec{a}.\]Všechny kostky se pohybují se stejným zrychlením.
Abychom mohli pohybové rovnice přepsat skalárně, zvolíme si souřadný systém os x,y tak, že osu x zvolíme ve směru pohybu kostek. Osa y je kolmá na osu x:
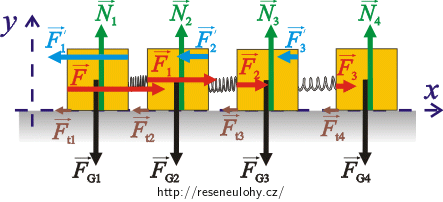
Pohybové rovnice pro jednotlivé kostky skalárně:
\[m_\mathrm{1_x}:\qquad F-F_\mathrm{t}-F_1\prime\,=\,ma,\tag{1}\] \[m_\mathrm{2_x}:\qquad F_1-F_\mathrm{t}-F_2\prime\,=\,ma,\tag{2}\] \[m_\mathrm{3_x}:\qquad F_2-F_\mathrm{t}-F_3\prime\,=\,ma,\tag{3}\] \[m_\mathrm{4_x}:\qquad F_3-F_\mathrm{t}\,=\,ma.\tag{4}\]Pohybové rovnice ve směru osy y jsou pro všechny čtyři kostky stejné:
\[m_\mathrm{y}:\qquad N-F_\mathrm{G}\,=\,0.\tag{5}\]Kostka m1 působí prostřednictvím první pružiny na kostku m2 a naopak kostka m2 působí prostřednictvím stejné pružiny na kostku m1. Obdobně je tomu s kostkami m2, m3 a m3, m4. Podle 3. Newtonova zákona platí pro velikosti sil:
\[|\vec{F}_1| = |\vec{F}_1\prime|,\] \[|\vec{F}_2| = |\vec{F}_2\prime|,\] \[|\vec{F}_3| = |\vec{F}_3\prime|.\]Přepíšeme rovnice (1) - (4):
\[m_\mathrm{1_x}:\qquad F-F_\mathrm{t}-F_1\,=\,ma,\tag{6}\] \[m_\mathrm{2_x}:\qquad F_1-F_\mathrm{t}-F_2\,=\,ma,\tag{7}\] \[m_\mathrm{3_x}:\qquad F_2-F_\mathrm{t}-F_3\,=\,ma,\tag{8}\] \[m_\mathrm{4_x}:\qquad F_3-F_\mathrm{t}\,=\,ma.\tag{9}\]Vyjádření třecí síly:
Třecí síla působící na kostku je úměrná tlakové síle, kterou každá kostka působí na podložku. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí podložka na kostku. Zapíšeme to rovnicí:
\[F_\mathrm{t}\,=\,fN.\]Sílu N vyjádříme z rovnice (5):
\[N\,=\,F_\mathrm{G}.\]Pro třecí sílu platí:
\[F_\mathrm{t}\,=\,fF_\mathrm{G}\,=\,mgf.\tag{10}\]Sečtěme rovnice (6) - (9) a vyjádřeme sílu F:
\[F-4F_\mathrm{t}\,=\,4ma,\] \[F\,=\,4ma+4F_\mathrm{t}.\]Dosadíme za třecí sílu ze vztahu (10):
\[F\,=\,4ma+4mgf\,=\,4m\left(a+gf\right).\tag{11}\]Vyjádření sil působících na pružiny:
Sílu působící na první pružinu spočteme tak, že sečteme rovnice (7), (8) a (9):
\[F_1-3F_\mathrm{t}\,=\,3ma,\] \[F_1\,=\,3ma+3mgf\,=\,3m\left(a+gf\right).\tag{12}\]Sílu působící na druhou pružinu spočteme tak, že sečteme rovnice (8) a (9):
\[F_2-2F_\mathrm{t}\,=\,2ma,\] \[F_2\,=\,2ma+2mgf\,=\,2m\left(a+gf\right).\tag{13}\]Sílu působící na třetí pružinu vyjádříme z rovnice (9):
\[F_3\,=\,ma+mgf\,=\,m\left(a+gf\right).\tag{14}\]Zkrácení pružin:
Síla stlačující pružinu je úměrná jejímu zkrácení Δl a také tuhosti pružiny k. Vztah pro sílu stlačující pružinu:
\[F\,=\,k\Delta l.\]Vyjádříme zkrácení:
\[\Delta l\,=\,\frac{F}{k}.\]Výpočet zkrácení pro jednotlivé pružiny:
\[\Delta l_1=\frac{F_1}{k}\,=\,\frac{3m\left(a+gf\right)}{k},\tag{15}\] \[\Delta l_2=\frac{F_2}{k}\,=\,\frac{2m\left(a+gf\right)}{k},\tag{16}\] \[\Delta l_3=\frac{F_3}{k}\,=\,\frac{m\left(a+gf\right)}{k}.\tag{17}\]CELKOVÁ ODPOVĚĎ
Velikost síly F je \[F\,=\,4m\left(a+gf\right).\]
První pružina je zkrácena o délku \[\Delta l_1\,=\,\frac{F_1}{k}\,=\,\frac{3m\left(a+gf\right)}{k}.\]
Druhá pružina je zkrácena o délku \[\Delta l_2\,=\,\frac{F_2}{k}\,=\,\frac{2m\left(a+gf\right)}{k}.\]
Třetí pružina je zkrácena o délku \[\Delta l_3\,=\,\frac{F_3}{k}\,=\,\frac{m\left(a+gf\right)}{k}.\]





