Problém s trámem
Úloha číslo: 513
Dva muži nesou na ramenech homogenní dřevěný trám o délce L = 6 m. Jeden z mužů podpírá trám na jeho konci. Jak daleko od druhého konce podpírá trám druhý muž, tlačí-li trám na jeho rameno silou o 50 % větší než na rameno prvního muže?
Zápis
L = 6 m délka trámu r1 = 3 m vzdálenost mezi místem, ve kterém podpírá trám první muž, a středem trámu F1 síla, kterou podepírá trám první muž F2 =1,5·F1 síla, kterou podepírá trám druhý muž r2 = ? (m) vzdálenost mezi místem, ve kterém podpírá trám druhý muž, a středem trámu Nápověda 1
Co vyplývá pro síly působící na trám z faktu, že trám mužům nepadá, ani se nijak neotáčí?Nápověda 2
Nakreslete si obrázek situace a vyznačte všechny síly působící na trám. Nepřipomíná vám jeden z jednoduchých strojů? Zapište si obě podmínky rovnováhy.Celkové řešení
Působící síly udržují trám v rovnováze. Situace je podobná rovnováze na dvojzvratné páce či vahadlu. Při rovnováze musí platit, že výslednice sil působících na trám musí být nulový vektor a také výslednice momentů těchto sil musí být rovna nule (vzhledem k libovolnému bodu).
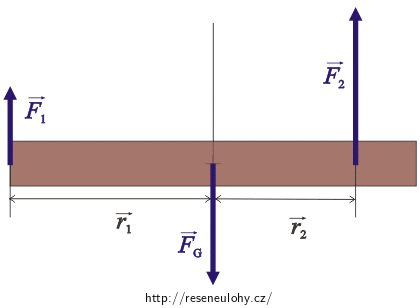
Pro síly tedy platí:
\[\vec{F}_1+\vec{F}_2+\vec{F}_\mathrm{G}=\vec{0}\,.\]Přepíšeme skalárně:
\[{F}_1+{F}_2-{F}_\mathrm{G}={0}\,.\]Pro momenty sil vzhledem k těžišti platí:
\[\vec{M}_1+\vec{M}_2=\vec{0}\,.\]Přepíšeme skalárně (za kladný vezmeme M1):
\[{M}_1-{M}_2=0\,.\]Pro velikosti momentů platí:
\[{F}_1 {r}_1 = {F}_2 {r}_2\,,\tag{1}\]kde r1 a r2 jsou vzdálenosti mezi těžištěm a místem působení síly, moment tíhové síly je vzhledem k těžišti nulový.
Víme, že:
\[F_2=\frac{3}{2} F_1\,,\] \[r_1=\frac{L}{2}\,.\]Dosadíme za F2 a r1 do vztahu (1) a vyjádříme vzdálenost r2:
\[F_1\frac{L}{2}=\frac{3}{2} F_1r_2\,,\] \[r_2=\frac{L}{3}\,.\]Číselně:
Je dáno L = 6 m,
\(r_2=\frac{1}{3}\cdot6 \mathrm{m}=2 \mathrm{m}\,.\)Druhý muž nese trám 2 metry od středu, tj. 1 metr od konce.
Odpověď
Druhý muž nese trám 2 metry od středu, tj. 1 metr od konce.



