Moment setrvačnosti dvou kuliček
Úloha číslo: 1129
Dvě malé homogenní kuličky o hmotnostech m1, m2 jsou spojeny tyčí o délce L, jejíž hmotnost můžeme zanedbat. Určete moment setrvačnosti Jo soustavy vzhledem k ose o, která je kolmá na tyč a prochází těžištěm soustavy.
Zápis
m1 hmotnost 1. kuličky m2 hmotnost 2. kuličky L délka spojovací tyče Jo = ? moment setrvačnosti soustavy vzhledem k ose procházející těžištěm Nápověda 1
Na úvod si situaci nakreslete a vhodně umístěte do souřadného systému. Oběma kuličkám v něm připište odpovídající souřadnice. Vzhledem k tomu, že nebyly zadány jejich rozměry, můžeme považovat kuličky za hmotné body, jejichž hmotnost je soustředěna ve středech (tedy i těžištích) původních koulí.
Nápověda 2
Máme určit moment setrvačnosti Jo soustavy vzhledem k ose o procházející jejím těžištěm – musíme tedy nejdříve určit souřadnice samotného těžiště T. Připomeňte si vztah pro polohový vektor těžiště soustavy hmotných bodů.
Lze jednu ze souřadnic těžiště určit okamžitě bez počítání?
Nápověda 3
Určete vzdálenosti jednotlivých kuliček (hmotných bodů A a B) od těžiště soustavy. Umíte již pomocí těchto vzdáleností určit požadovaný moment setrvačnosti? Dopočítejte ho.
Celkové řešení
Vzhledem k tomu, že nebyly zadány rozměry kuliček, můžeme je považovat za hmotné body, jejichž hmotnost je soustředěna ve středech (tedy i těžištích) původních koulí.
Obrázek níže ukazuje naši situaci umístěnou vhodným způsobem do soustavy souřadnic. Obě kuličky leží na ose x, jedna z nich je umístěna přímo v počátku souřadného systému.
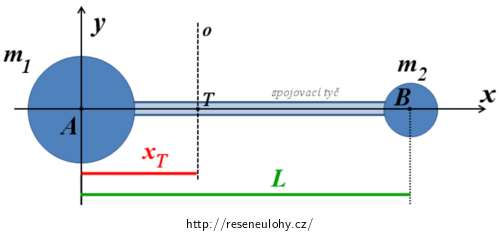
Souřadnice hmotných bodů A a B, které kuličky zastupují, jsou v našem případě:
\[A\,=\,[0{,}0],\] \[B\,=\,[L,0].\]Protože budeme zkoumat moment setrvačnosti vzhledem k ose procházející těžištěm, musíme nejdříve určit polohu těžiště. Vztah pro polohu těžiště soustavy n hmotných bodů vypadá následovně:
\[\vec{r}_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}\vec{r}_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}},\]kde mi jsou hmotnosti jednotlivých hmotných bodů a ri jim příslušející polohové vektory. Protože souřadnice těžiště lze počítat po složkách, platí pro x-ovou souřadnici těžiště naší soustavy:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}L}{m_1\,+\,m_2}\,=\,\frac{m_2L}{m_1\,+\,m_2}.\tag{1}\]Pro y-ovou souřadnici těžiště je možné opakovat tentýž postup, zde je ale výsledek na první pohled patrný – obě kuličky mají y-ovou souřadnici nulovou, tedy také yT = 0.
Z obrázku je nyní zřejmé, že vzdálenost bodu A od těžiště soustavy je xT, vzdálenost bodu B od těžiště je L − xT. Přitom vzdálenost od těžiště zde znamená také vzdálenost od osy o, která těžištěm kolmo k tyči prochází. Máme tedy vše, co potřebujeme k určení momentu setrvačnosti Jo.
Připomeňme ještě, že moment setrvačnosti soustavy n hmotných bodů je vzhledem k dané ose určen jako:
\[J\,=\,\sum_{i\,=\,1}^n{m_\mathrm{i}r_\mathrm{i}^2},\]kde mi jsou hmotnosti jednotlivých hmotných bodů a ri jejich vzdálenosti od dané osy. V našem případě jde o osu o a platí:
\[J_\mathrm{o}\,=\,m_1x_\mathrm{T}^2\,+\,m_2(L\,-\,x_\mathrm{T})^2.\tag{2}\]Za xT dosadíme ze vztahu (1) a dostáváme:
\[J_\mathrm{o}\,=\,m_1(\frac{m_2L}{m_1\,+\,m_2})^2\,+\,m_2(L\,-\,\frac{m_2L}{m_1\,+\,m_2})^2,\] \[J_\mathrm{o}\,=\,\frac{m_1m_2^2L^2}{(m_1\,+\,m_2)^2}\,+\,m_2L^2(1\,-\,\frac{m_2}{m_1\,+\,m_2})^2,\] \[J_\mathrm{o}\,=\,\frac{m_1m_2^2L^2}{(m_1\,+\,m_2)^2}\,+\,\frac{m_2L^2m_1^2}{(m_1\,+\,m_2)^2}\,=\frac{m_1m_2L^2(m_1\,+\,m_2)}{(m_1\,+\,m_2)^2},\] \[J_\mathrm{o}\,=\,\frac{m_1m_2L^2}{m_1\,+\,m_2}.\]Odpověď
Moment setrvačnosti Jo uvedené soustavy vzhledem k ose o procházející jejím těžištěm je:
\[J_\mathrm{o}\,=\,\frac{m_1m_2L^2}{m_1\,+\,m_2}.\]



