Bójka na hladině
Úloha číslo: 2211
Na hladině vody plave bójka, která má tvar koule, o hmotnosti \(m\) a objemu \(10\,\mathrm{{cm}^3}\). Bójka je z poloviny ponořená ve vodě. Na vlákně je k ní upoutána druhá koule téhož objemu a hmotnosti \(M=3m\). Určete velikost síly, kterou je vlákno napínáno.
Zápis a nákres

hmotnost koule na hladině…\(m\)
hmotnost koule ponořené…\(M = 3m\)
objem koule…\(V = 10\,\mathrm{{cm}^3}\)
velikost síly, kterou je napínáno vlákno…\(F =\,?\,\)
Nápověda
Rozmyslete si, jaké všechny síly působí na každou z koulí. Zakreslete si působící síly do nákresu. Co musí platit pro výslednice?
Řešení
Nejprve si zakreslíme síly působící na bójky (viz obr. 2). Na obě působí tíhová síla – označme tíhovou sílu působící na kouli na hladině \(\vec {F_\mathrm{G}}\) a na zcela ponořenou kouli \(\vec {F_\mathrm{G}'}\). Stejný čárkovaný způsob značení budeme používat i nadále.
Další silou působící na obě koule je vztlaková síla, označme ji \(\vec {F_\mathrm{V}}\). Ta bójky ve vodě „nadnáší“.
Poslední silou je síla \(\vec {F}\), kterou za bójky táhne provázek. Horní táhne směrem dolů, spodní směrem nahoru. Velikost síly \(\vec {F}\) máme určit.
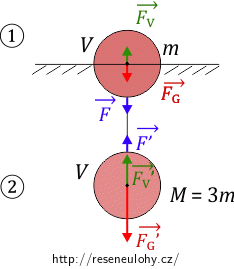
Výslednice sil působící na horní i dolní bójku je nulová, protože se bójky ani nepotápí, ani nevylétávají z vody ven, ale zůstávají v klidu, tj. síly jsou v rovnováze. Podívejme se na rovnováhu sil pro kouli na hladině (na obrázku pod číslem 1). Tíhová síla \(\vec {F_\mathrm{G}}\) a tahová síla provázku \(\vec {F}\) působí stejným směrem, opačným směrem působí vztlaková síla \(\vec {F_\mathrm{V}}\). Zapíšeme to do rovnice:
\[ F + F_\mathrm{G} = F_\mathrm{V}. \]
Dosadíme za velikosti jednotlivých sil. Hmotnost koule je \(m\), tíhové zrychlení označíme \(g\), objem ponořené části koule je \(\frac{1}{2}V\).
\[ F + mg = \frac{1}{2}V\rho g, \]
kde \(\rho\) je hustota vody.
Stejným způsobem sestavíme silovou rovnici pro druhou kouli a dosadíme:
\[ F' + F_\mathrm{V}' = F_\mathrm{G}', \]
\[ F' + V\rho g = Mg. \]
Ze zadání víme, že \(M=3m\). Síla, kterou prostřednictvím provázku tahá horní koule za spodní, musí být podle 3. Newtonova zákona stejně velká jako ta, kterou tahá spodní za horní. Můžeme napsat \(F'= F\). Dosadíme za \(M\) a \(F'\), získáme soustavu rovnic, kterou budeme dále řešit:
\[ F + mg = \frac{1}{2}V\rho g, \tag{1}\]
\[ F + V\rho g = 3mg. \tag{2}\]
První rovnici (1) vynásobíme třemi a přičteme k druhé (2). Dostaneme rovnici o jedné neznámé, kterou vyjádříme:
\[ 4F + 3mg + V\rho g = \frac{3}{2}V\rho g + 3mg, \]
\[ 4F = \frac{3}{2}V\rho g − V\rho g, \]
\[ F = \frac{1}{8}V\rho g. \]
Do získaného výrazu dosadíme \(V = 10^{-5}\,\mathrm{m^3}\), \(\rho = 1000\,\mathrm{\frac{kg}{m^3}}\), \(g = 9{,}81\,\mathrm{ms^{-2}}\):
\[F = \frac{10^{-5}\cdot1000{\cdot} 9{,}81}{8} \mathrm{N} \doteq 1{,}2 {\cdot} 10^{-2}\,\mathrm{N} \]
Odpověď
Síla \(\vec {F}\), kterou je napínáno vlákno, má velikost \(1{,}2{\cdot}10^{-2}\,\mathrm {N}\).
Jak udělat správný nákres
Při zakreslování sil si nejprve rozeberte celou situaci. Jaké všechny síly budou působit, kde mají působiště atd.
Správně nakreslený obrázek mnohdy usnadní úlohu a pomůže vám najít řešení, stejně jako špatný obrázek může vést k počítání s předpoklady, které podle zadání neplatí.
V této úloze si například můžeme po přečtení zadání všimnout, že tíhová síla působící na kouli s třikrát větší hmotností, bude také třikrát větší. Když tedy budeme do obrázku vyznačovat tíhovou sílu, bude šipka u zcela ponořené koule třikrát delší, než u té na hladině. Samozřejmě šipku zakreslíme svisle dolů, s počátkem v těžišti tělesa.
Podobným způsobem můžeme uvažovat i při kreslení ostatních sil. Z horní bójky je ponořena do vody polovina, spodní je ponořená celá. Vztlaková síla působící na horní bójku bude mít poloviční velikost než u spodní. Tahové síly provázku působící na bójky mají podle 3. Newtonova zákona stejnou velikost a jsou opačně orientované.
Samozřejmě není nutné zachovávat poměr délky šipek na milimetry, taková přesnost je v případě potřeby rychlého náčrtku téměř zbytečná.

