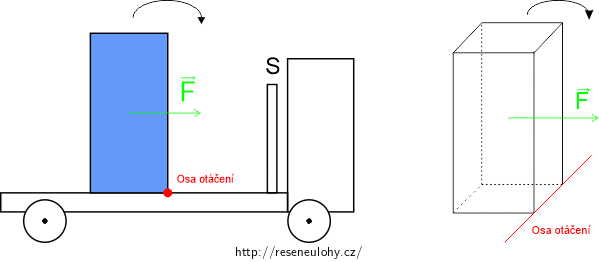
Pohybující se vozík s přepravkou

Úloha číslo: 4499

Na nákladním vozíku je přepravka o tvaru kvádru s šířkou 1,0 m, délkou 1,0 m a výškou 2,0 m. Těžiště přepravky je v jejím geometrickém středu. Hmotnost přepravky je 400 kg. Koeficient statického tření mezi dnem nákladního vozíku a dnem přepravky je 0,40. Vozík zrychluje rovnoměrně z klidu na 50 km/h, vzdálenost kterou během zrychlení ujede, je 150 m.

a) Vypočítejte tíhovou sílu působící na přepravku.

b) Vypočítejte zrychlení vozíku.

c) Vypočítejte kinetickou energii, kterou přepravka během daného zrychlování získá. Předpokládejme stejnou rychlost vozíku a přepravky během zrychlování.

d) Dno nákladního prostoru je vodorovné, přepravka stojí ve středu dna, neopírá se o boky nákladního prostoru. Výpočtem potvrďte, že se přepravka nesmýká po dnu nákladního prostoru. S využitím výpočtu slovně popište, proč tvrzení platí.

e) Vypočítejte zpomalení nákladního vozíku, při kterém by se přepravka začala smýkat po dnu nákladní plochy. Postup výpočtu slovně zdůvodněte.

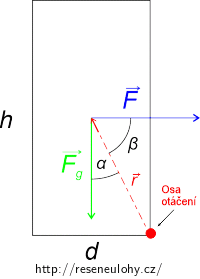
f) Vypočítejte velikost momentu síly, kterým byste museli působit na přepravku, aby se překlopila přes přední hranu (viz obrázek 1). Jak velká síla, která má vodorovný směr a působí v těžišti, by při tom musela působit?

obrázek 1: vlevo náčrtek úlohy, vpravo náčrtek přepravky

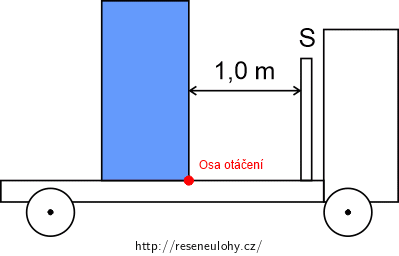
g) Nákladní vozík jede rychlostí 50 km/h. Přepravka je umístěná v nákladním prostoru vozíku ve vzdálenosti 1,0 m od boku nákladního prostoru S (viz obrázek 2). Potom začne vozík brzdit a přepravka se smýká vzhledem ke spodku nákladního prostoru se zrychlením 2,6 m·s^-2 a narazí do stěny S dříve, než se vozík zastaví. Vypočítejte velikost impulzu síly při nárazu přepravky do stěny S nákladního prostoru vozíku. Přepravka při nárazu do stěny neodskočí.

Zápis

l = 1,0 m	délka přepravky
w = 1,0 m	šířka přepravky
h = 2,0 m	výška přepravky
m = 400 kg	hmotnost přepravky
f = 0,40	koeficient statického tření mezi dnem vozíku a přepravky
v₁ = 50 km/h = 13,9 m·s^-1	konečná rychlost vozíku
s₁ = 150 m	dráha, během které vozík zrychlí z klidu na v₁
s₂ = 1,0 m	vzdálenost přepravky od boku nákladního prostoru v úloze g)
a₂ = 2,6 m·s^-2	zrychlení přepravky v úloze g)

a) F_G = ?	tíhová síla působící na přepravku
b) a₁ = ?	zrychlení vozíku
c) E_k = ?	kinetická energie přepravky
e) a_z = ?	zpomalení vozíku
f) F = ?	velikost síly nutné k překlopení přepravky
M = ?	velikost momentu síly nutného k překlopení přepravky
g) I = ?	velikost impulsu síly

g = 9,81 m·s^-2

tíhové zrychlení

Nápověda a: tíhová síla působící na přepravku
Pomocí jakého vztahu můžeme vypočítat tíhovou sílu působící na těleso? Jaké veličiny k tomu musíme znát?
Řešení nápovědy a: tíhová síla na přepravku
Tíhovou sílu určíme ze vztahu: \[F_G = mg, \] kde m je hmotnost tělesa a g tíhové zrychlení. \[F_G = mg = 400 \ \text{kg} \cdot 9{,}81 \ \text{m}\cdot \text{s}^{-2} = 3920 \ \text{N.}\]
Nápověda b: zrychlení vozíku
Jak můžeme vyjádřit vzdálenost, kterou těleso ujede při rovnoměrně zrychleném pohybu za čas t₁, když se pohybuje se zrychlením a₁?

Čas t₁ sice neznáme, ale můžeme si ho vyjádřit pomocí konečné rychlosti v₁ a zrychlení a₁.

Dokázali byste pomocí těchto dvou vztahů vyjádřit zrychlení a₁?
Řešení nápovědy b: zrychlení vozíku
Pro dráhu rovnoměrně zrychleného pohybu platí
\[s_1 = \frac{1}{2}a_1t_1^2.\]
Při rovnoměrně zrychleném pohybu platí pro rychlost v₁ = a₁t₁. Vyjádřením t₁ z tohoto vztahu a dosazením do vztahu pro dráhu dostáváme:
\[s_1 = \frac{1}{2}a_1\frac{v_1^2}{a_1^2} = \frac{v_1^2}{2a_1} \rightarrow a_1 = \frac{v_1^2}{2s_1} = \frac{(13{,}9 \ \text{m}\cdot \text{s}^{-1})^2}{2{\cdot} 150 \ \text{m}} \, \dot =\, 0{,}64 \ \text{m}\cdot \text{s}^{-2}\]
Nápověda c: kinetická energie
Pomocí jakého vztahu můžeme vypočítat kinetickou energii tělesa o hmotnosti m a rychlosti v₁?
Řešení nápovědy c: kinetická energie
Pro kinetickou energii platí vztah:
\[E_k = \frac{1}{2}mv_1^2 = \frac{1}{2}\cdot 400 \ \text{kg} \cdot (13{,}9 \ \text{m} \cdot \ \text{s}^{-1})^2 \, \dot =\, 38{,}6 \ \text{kJ.}\]
Nápověda d: smýkání přepravky
Přepravka zrychluje spolu s vozíkem, musí na ni tedy působit nenulová výsledná síla. Jaká síla urychluje přepravku? Jaká je její velikost?

Jaká je maximální možná velikost, kterou může tato síla dosáhnout?

Co se stane, když zrychlení vozíku bude takové, že tato síla již nebude stačit, aby přepravce takové zrychlení udělila?
Řešení nápovědy d: smýkání přepravky
Přepravka zrychluje s vozíkem díky působení klidové třecí síly mezi dnem vozíku a dnem přepravky. Její velikost je: \(F_t = ma = 400 \ \text{kg} \cdot 0{,}64 \ \text{m}\cdot \text{s}^{-2} = 256 \ \text{N}\).

Pro maximální klidovou třecí sílu platí \(F_{tm} = fF_N = fmg = 0{,}40 {\cdot} 3920 \ \text{N} = 1568 \ \text{N.}\)

Klidová třecí síla, která působí na přepravku během zrychlování, je tedy menší než maximální klidová třecí síla, která může působit mezi přepravkou a dnem. Přepravka se tedy nebude smýkat po dně nákladního prostoru, bude vzhledem k němu v klidu.

Pokud by zrychlení vozíku bylo takové, že by síla potřebná na odpovídající zrychlení přepravky přesáhla hodnotu maximální klidové třecí síly, přepravka by se začala po dně vozíku smýkat.
Nápověda e: smýkání přepravky při zpomalování
V minulé úloze jsme zjistili maximální hodnotu klidové třecí síly, která může urychlovat přepravku, aby se ještě nesmýkala. Obdobně je to se zpomalováním přepravky. Spočítejte s pomocí známé maximální klidové třecí síly odpovídající maximální zrychlení, se kterým se může přepravka rozjíždět nebo brzdit, aniž by se smýkala.
Řešení nápovědy e: smýkání přepravky při zpomalování
Aby se přepravka začala smýkat, musí být síla potřebná na její zpomalování větší než maximální klidová třecí síla působící mezi dnem vozíku a dnem přepravky, musí tedy platit
\[ma_{z} \geq F_{tm} \rightarrow a_z \geq \frac{F_{tm}}{m} = \frac{1568 \ \text{N}}{400 \ \text{kg}} = 3{,}92 \ \text{m}\cdot \text{s}^{-2},\]
kde a_z je kritická hodnota zpomalení.
Nápověda f: překlápění přepravky
Připomeňte si vztah pro výpočet momentu síly. Která síla drží přepravku při zemi a brání nám v jejím překlápění?

Udělejte si náčrtek přepravky, vyznačte do něj osu otáčení a tíhovou sílu působící na přepravku. Vyjádřete její moment vzhledem k ose otáčení.

Dále si do obrázku nakreslete vodorovnou sílu F a vyjádřete její moment vzhledem k ose otáčení.
Řešení nápovědy f: překlápění přepravky
Při překlopení přepravky musíme překonat moment tíhové síly vzhledem k ose otáčení, ten je roven
\[\overrightarrow{M}_{F_G} = \overrightarrow{r} \times \overrightarrow{F}_G\] \[M_{F_G} = rF_G\sin(\alpha) = rmg\frac{\frac{d}{2}}{r} = mg\frac{d}{2}\]
Moment síly F je roven
\[M = |\overrightarrow{M}| = |\overrightarrow{r} \times \overrightarrow{F}| = rF \ \sin(\beta) = rF\frac{\frac{h}{2}}{r} = F\frac{h}{2}\]

Pro velikost síly F pak musí platit
\[|\overrightarrow{M}_{F_G}| = |\overrightarrow{M}|,\] \[|\overrightarrow{r} \times \overrightarrow{F}_G| = |\overrightarrow{r} \times \overrightarrow{F}|,\] \[mg\frac{d}{2} = F\frac{h}{2} \rightarrow F = \frac{d}{h}mg = \frac{1}{2}\cdot 400 \ \text{kg} \cdot 9{,}81 \ \text{m}\cdot \text{s}^{-2} = 1962 \ \text{N},\]
Dosazením F do vzorce pro M dostaneme
\[M = F\frac{h}{2} = 1962 \ \text{N} \cdot \frac{2{,}0 \ \text{m}}{2} = 1962 \ \text{N} \cdot \text{m}.\]
Moment síly \(\overrightarrow{M}\) je (dle definice vektorového součinu) kolmý na vektor \(\overrightarrow{r}\) a sílu \(\overrightarrow{F}\), je tedy rovnoběžný s osou otáčení. Směr momentu síly \(\overrightarrow{M}\) určíme pomocí pravidla pravé ruky: je kolmý na boční stěnu přepravky, jeho směr je souhlasný s osou otáčení, směřuje kolmo za nákresnu.
Nápověda g: impuls síly
Připomeňte si, jak je definován impuls síly a čemu je roven. Zjistěte, jakou rychlostí narazí přepravka do strany S.
Řešení nápovědy g: impuls síly
Impuls síly je fyzikální veličina popisující časový účinek síly, je roven změně hybnosti tělesa. Platí:
\[I = F\Delta t = ma\Delta t = m\Delta v\]
Přepravka se při brzdění vozíku začne rozjíždět z klidu se zadaným zrychlením po dráze s₂ = 1,0 m. Pro rychlost, kterou na této dráze dosáhne, platí: \(v_2 = a_2\cdot t_2\).

Čas vyjádříme ze vztahu \(s_2 = \frac{1}{2}a_2t_2^2 \rightarrow t_2 = \sqrt{\frac{2s_2}{a_2}}.\)
\[v_2 = a_2t_2 = a_2\sqrt{\frac{2s_2}{a_2}} = \sqrt{2a_2s_2} = \sqrt{2 \ \cdot \ 1 \ \text{m} \cdot 2{,}6 \ \text{m}\cdot \text{s}^{-2}}\] \[I = mv_2 = 400 \ \text{kg} \cdot \sqrt{2 \ \cdot \ 1 \ \text{m} \cdot 2{,}6 \ \text{m}\cdot \text{s}^{-2}} \, \dot =\, 912 \ \text{N}\cdot \text{s.}\]

Odpovědi

a)	Tíhová síla působící na přepravku je F_G = 3920 N.
b)	Zrychlení vozíku je a₁ \(\dot{=}\) 0,64 m·s^-2.
c)	Během daného zrychlování získá přepravka kinetickou energii E_k \(\dot{=}\) 38,6 kJ.
d)	Klidová třecí síla F_t = 256 N je menší než maximální klidová třecí síla F_tm = 1568 N. Přepravka se tedy nebude smýkat po dnu.
e)	Přepravka se začne smýkat po dnu nákladní plochy při zpomalení a_z = 3,92 m·s^-2.
f)	Aby se přepravka překlopila, museli bychom na ní v těžišti působit silou o velikosti F = 1962 N ve vodorovném směru. Moment síly by měl velikost M = 1962 N·m.
g)	Velikost impulzu síly při nárazu přepravky do stěny S nákladního prostoru vozíku je I \(\dot{=}\) 912 N·s.