Loďky

Úloha číslo: 167

Na hladině vody jsou dvě loďky v klidu záděmi u sebe. V každé z nich sedí chlapec. Chlapec v první loďce o celkové hmotnosti m₁ tlačí pádlem konstantní silou po dobu Δt do druhé loďky o celkové hmotnosti m₂. Druhá loďka tak dosáhne vzhledem k hladině vody rychlosti o velikosti v₂.

a) Určete konečnou velikost vzájemné rychlosti v obou loděk.

b) Určete velikost F síly, kterou chlapec působil.

c) Určete změnu vzdálenosti Δs mezi loďkami během silového působení chlapce.

d) Určete práci W vykonanou během odstrkování loděk.

e) Určete poměr kinetických energií druhé a první loďky.

Odporové síly zanedbejte. Řešte nejprve obecně, pak pro hodnoty:

m₁ = 240 kg, m₂ = 160 kg, v₂ = 0,90 m·s^-1, Δt = 1,5 s.

Zápis

m₁ = 240 kg	hmotnost první loďky
m₂ = 160 kg	hmotnost druhé loďky
v₂ = 0,90 m·s^-1	rychlost druhé loďky
Δt = 1,5 s	doba, po kterou chlapec v první loďce tlačí do druhé loďky
v = ? (m·s^-1)	vzájemná rychlost loďek
F = ? (N)	síla, kterou působí chlapec
Δs = ? (m)	změna vzdálenosti mezi loďkami během silového působení chlapce
W = ? (J)	práce vykonaná během odstrkování loďek
\(\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\) = ?	poměr kinetických energií loděk

Nápověda a - zákon zachování hybnosti
Nakreslete si obrázek. Vyjádřete si ze zákona zachování hybnosti (ZZH) rychlost první loďky. Jak spočítáte vzájemnou rychlost obou loděk?
Řešení k nápovědě a - zákon zachování hybnosti

Podle zákona zachování hybnosti platí, že hybnost loděk před odstrčením bude rovna jejich hybnosti po odstrčení.
\[\mathrm{ZZH}: \qquad \vec{p_{01}}+\vec{p_{02}}=\vec{p_1}+\vec{p_2}\]
\(\vec{p_{01}}\)… hybnost první loďky s chlapcem před odstrčením (p₀₁ = 0)

\(\vec{p_{02}}\)…hybnost druhé loďky s chlapcem před odstrčením (p₀₂ = 0)

\(\vec{p_1}\)…hybnost první loďky s chlapcem po odstrčení

\(\vec{p_2}\)…hybnost druhé loďky s chlapcem po odstrčení
\[0=m_1\vec{v_1}+m_2\vec{v_2}\]
\(m_1\)…hmotnost první loďky s chlapcem

\(m_2\)…hmotnost druhé loďky s chlapcem

\(v_1\)…rychlost první loďky s chlapcem po odstrčení

\(v_2\)…rychlost druhé loďky s chlapcem po odstrčení

Předpokládejme, že se loďky pohybují po přímce. Rovnici přepíšeme skalárně:
\[m_1v_1-m_2v_2\,=\,0.\]
Vyjádříme si rychlost v₁:
\[v_1\,=\,\frac{m_2v_2}{m_1}.\tag{1}\]
Loďky se pohybují od sebe, takže jejich vzájemnou rychlost získáme, sečteme-li rychlost první loďky s rychlostí druhé loďky:
\[v\,=\,v_1+v_2,\]
\(v\)…vzájemná rychlost obou loděk.

Za rychlost v₁ dosadíme ze vztahu (1):
\[v\,=\,\frac{m_2v_2}{m_1}+v_2,\] \[v\,=\,\frac{m_1+m_2}{m_1}v_2.\tag{2}\]
Nápověda b - velikost působící síly
Chlapec působí na 2. loďku stálou silou F po dobu Δt. Během tohoto působení se změní hybnost 2. loďky o Δp. Zkuste to zapsat pomocí druhého Newtonova zákona.
Řešení k nápovědě b - velikost působící síly
Druhý Newtonův zákon můžeme v naší situaci zapsat ve tvaru:
\[F\,=\,\frac{\Delta p}{\Delta t},\]
\(F\)…síla, kterou chlapec na první loďce působí na druhou loďku,

\(\Delta t\)…čas, po který působí chlapec na první loďce sílou F na druhou loďku,

\(\Delta p\)…změna hybnosti 2. loďky,
\[\Delta p\,=\,m_2v_2-0,\] \[F\,=\,\frac{m_2v_2}{\Delta t}.\]
Nápověda c - změna vzdálenosti loděk
Jakým pohybem se pohybují loďky vzhledem k hladině při odstrkování? Jakou vzdálenost přitom urazí?
Řešení k nápovědě c - změna vzdálenosti loděk
Loďky se během odstrkování pohybují vzhledem k hladině rovnoměrně zrychleným pohybem.

První loďka urazí vzdálenost s₁:
\[s_1\,=\,\frac{1}{2}a_1(\Delta t)^2.\]
Zrychlení a₁ můžeme vyjádřit jako:
\[a_1\,=\,\frac{v_1}{\Delta t},\] \[s_1\,=\,\frac{1}{2}v_1\Delta t.\]
Druhá loďka urazí vzdálenost s₂:
\[s_2\,=\,\frac{1}{2}a_2(\Delta t)^2.\]
Zrychlení a₂ můžeme vyjádřit jako:
\[a_2\,=\,\frac{v_2}{\Delta t},\] \[s_2\,=\,\frac{1}{2}v_2\Delta t.\]
Celkově se loďky vzdálí během působení o vzdálenost Δs:
\[\Delta s\,=\, s_1+s_2\,=\,\frac{1}{2}v_1\Delta t+\frac{1}{2}v_2\Delta t.\]
Za rychlost v₁ dosadíme ze vztahu (1):
\[\Delta s\,=\,\frac{1}{2}\frac{m_2v_2}{m_1}\Delta t+\frac{1}{2}v_2\Delta t,\] \[\Delta s\,=\,\frac{m_1+m_2}{2m_1}v_2\Delta t. \]
Situaci můžeme také řešit v soustavě spojené například s první loďkou.

V této soustavě se druhá loďka vzdaluje rovnoměrně zrychleným pohybem a za dobu Δt dosáhne konečné rychlosti o velikosti v. Změna vzdálenosti je:
\[\Delta s\,=\,\frac{1}{2}v\Delta t,\]
\(\Delta s\)…změna vzdálenosti druhé loďky od první.

Za rychlost v dosadíme ze vztahu (2):
\[\Delta s\,=\, \frac {m_1+m_2}{2m_1}v_2\Delta t.\tag{3}\]
Nápověda d - vykonaná práce
Na co se promění práce vykonaná během odstrkování loděk? Vyjádřete to vztahem.
Řešení k nápovědě d - vykonaná práce
Práce vykonaná během odstrkování loděk se projeví vzrůstem kinetické energie obou loděk. (Změny vnitřní energie neuvažujeme.)
\[W\,=\,E_\mathrm{k1}+E_\mathrm{k2}\]
\(W\)…vykonaná práce

\(E_\mathrm{k1}\)…kinetická energie první loďky s chlapcem

\(E_\mathrm{k2}\)…kinetická energie druhé loďky s chlapcem
\[W\,=\,\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\]
Za rychlost v₁ dosadíme ze vztahu (1):
\[W\,=\,\frac{1}{2}m_1\frac{m_2^2v_2^2}{m_1^2}+\frac{1}{2}m_2v_2^2,\] \[W\,=\,\frac{m_2^2v_2^2}{2m_1}+\frac{m_2v_2^2}{2},\] \[W\,=\,\frac{m_2(m_1+m_2)}{2m_1}v_2^2.\]
Nápověda e - poměr kinetických energií
Vyjádřete poměr kinetické energie druhé loďky E_k2 ke kinetické energii první loďky E_k1.
Řešení k nápovědě e - poměr kinetických energií
Poměr kinetické energie E_k2 ke kinetické energii E_k1 je:
\[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{\frac{1}{2}m_2v_2^2}{\frac{1}{2}m_1v_1^2},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{m_2v_2^2}{m_1\frac{m_2^2v_2^2}{m_1^2}},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{m_1}{m_2}.\]
Číselný výpočet
Je dáno:
\[m_1\,=\,240\,\mathrm{kg},\] \[m_2\,=\,160\,\mathrm{kg},\] \[v_2\,=\,0{,}9\,\mathrm{m \cdot s^{-1}},\] \[\Delta t\,=\,1{,}5\,\mathrm{s}.\]
a) hledáme:
\[v\,=\,?,\] \[v\,=\,\frac{m_1+m_2}{m_1}v_2,\] \[v\,=\,\frac{240+160}{240}\cdot 0{,}9\,\mathrm{m \cdot s^{-1}},\] \[v\,=\,1{,}5\,\mathrm{m \cdot s^{-1}}.\]
b) hledáme:
\[F\,=\,?,\] \[F\,=\,\frac{m_2v_2}{\Delta t},\] \[F\,=\,\frac{240{\cdot}0{,}9}{1{,}5}\,\mathrm{N},\] \[F\,=\,96\,\mathrm{N}.\]
c) hledáme:
\[\Delta s\,=\,?,\] \[\Delta s\,=\, \frac {m_1+m_2}{2m_1}v_2\Delta t,\] \[\Delta s\,=\, \frac {240+160}{2{\cdot}240}\cdot0{,}9{\cdot}1{,}5\,\mathrm{m},\] \[\Delta s\,=\, 1{,}1\,\mathrm{m}.\]
d) hledáme:
\[W\,=\,?,\] \[W\,=\,\frac{m_2(m_1+m_2)}{2m_1}v_2^2,\] \[W\,=\,\frac{160\cdot(240+160)}{2{\cdot}240}\cdot0{,}9^2\,\mathrm{J},\] \[W\,=\,108\,\mathrm{J}.\]
e) hledáme:
\[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,?,\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{m_1}{m_2},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{240}{160},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{3}{2}.\]
Odpověď
a) Konečná velikost vzájemné rychlosti obou loděk je \[v\,=\,\frac{m_1+m_2}{m_1}v_2\,=\,1{,}5\,\mathrm{m \cdot s^{-1}}.\]

b) Velikost síly, kterou chlapec na první loďcě působí na druhou loďku, je \[F\,=\,\frac{m_2v_2}{\Delta t}\,=\,96\,\mathrm{N}.\]

c) Změna vzdálenosti loděk během silového působení chlapce na první loďce je \[\Delta s\,=\, \frac {m_1+m_2}{2m_1}v_2\Delta t\,=\, 1{,}1\,\mathrm{m}.\]

d) Práce vykonaná během odstrkování loděk je rovna \[W\,=\,\frac{m_2(m_1+m_2)}{2m_1}v_2^2\,=\,108\,\mathrm{J}.\]

e) Poměr kinetických energií druhé a první loďky je \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{m_1}{m_2}\,=\,\frac{3}{2}.\]
Celkové řešení bodu a)

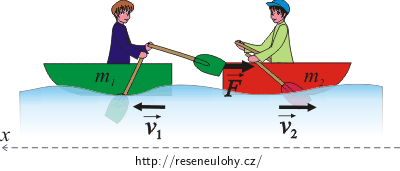
Podle zákona zachování hybnosti platí, že hybnost loděk před odstrčením bude rovna jejich hybnosti po odstrčení.
\[\mathrm{ZZH}: \qquad \vec{p_{01}}+\vec{p_{02}}=\vec{p_1}+\vec{p_2}\]
\(\vec{p_{01}}\)…hybnost první loďky s chlapcem před odstrčením (p₀₁ = 0)

\(\vec{p_{02}}\)…hybnost druhé loďky s chlapcem před odstrčením (p₀₂ = 0)

\(\vec{p_1}\)…hybnost první loďky s chlapcem po odstrčení

\(\vec{p_2}\)…hybnost druhé loďky s chlapcem po odstrčení
\[0=m_1\vec{v_1}+m_2\vec{v_2}\]
\(m_1\)…hmotnost první loďky s chlapcem

\(m_2\)…hmotnost druhé loďky s chlapcem

\(v_1\)…rychlost první loďky s chlapcem po odstrčení

\(v_2\)…rychlost druhé loďky s chlapcem po odstrčení

Předpokládejme, že se loďky pohybují po přímce. Rovnici přepíšeme skalárně:
\[m_1v_1-m_2v_2\,=\,0.\]
Vyjádříme si rychlost v₁:
\[v_1\,=\,\frac{m_2v_2}{m_1}.\tag{1}\]
Loďky se pohybují od sebe, takže jejich vzájemnou rychlost získáme, sečteme-li rychlost první loďky s rychlostí druhé loďky:
\[v\,=\,v_1+v_2,\]
\(v\)…vzájemná rychlost obou loděk.

Za rychlost v₁ dosadíme ze vztahu (1):
\[v\,=\,\frac{m_2v_2}{m_1}+v_2,\] \[v\,=\,\frac{m_1+m_2}{m_1}v_2,\tag{2}\] \[v\,=\,\frac{240+160}{240}\cdot0{,}9\,\mathrm{m \cdot s^{-1}},\] \[v\,=\,1{,}5\,\mathrm{m \cdot s^{-1}}.\]
Odpověď: Konečná velikost vzájemné rychlosti obou loděk je \[v\,=\,1{,}5\,\mathrm{m \cdot s^{-1}}.\]
Celkové řešení bodu b)
Druhý Newtonův zákon můžeme v naší situaci zapsat ve tvaru:
\[F\,=\,\frac{\Delta p}{\Delta t},\]
\(F\)…síla, kterou chlapec na první loďce působí na druhou loďku,

\(\Delta t\)…čas, po který působí chlapec na první loďce sílou F na druhou loďku,

\(\Delta p\)…změna hybnosti 2. loďky,
\[\Delta p\,=\,m_2v_2-0,\] \[F\,=\,\frac{m_2v_2}{\Delta t},\] \[F\,=\,\frac{240{\cdot}0{,}9}{1{,}5}\,\mathrm{N},\] \[F\,=\,96\,\mathrm{N}.\]
Odpověď: Velikost síly, kterou chlapec na první loďce působí na druhou loďku je \(F\,=\,96\,\mathrm{N}.\)
Celkové řešení bodu c)
Loďky se během odstrkování pohybují vzhledem k hladině rovnoměrně zrychleným pohybem.

První loďka urazí vzdálenost s₁:
\[s_1\,=\,\frac{1}{2}a_1(\Delta t)^2.\]
Zrychlení a₁ můžeme vyjádřit jako:
\[a_1\,=\,\frac{v_1}{\Delta t},\] \[s_1\,=\,\frac{1}{2}v_1\Delta t.\]
Druhá loďka urazí vzdálenost s₂:
\[s_2\,=\,\frac{1}{2}a_2(\Delta t)^2.\]
Zrychlení a₂ můžeme vyjádřit jako:
\[a_2\,=\,\frac{v_2}{\Delta t},\] \[s_2\,=\,\frac{1}{2}v_2\Delta t.\]
Celkově se loďky vzdálí během silového působení chlapce o vzdálenost Δs:
\[\Delta s\,=\, s_1+s_2\,=\,\frac{1}{2}v_1\Delta t+\frac{1}{2}v_2\Delta t.\]
Za rychlost v₁ dosadíme ze vztahu (1):
\[\Delta s\,=\,\frac{1}{2}\frac{m_2v_2}{m_1}\Delta t+\frac{1}{2}v_2\Delta t,\] \[\Delta s\,=\,\frac{m_1+m_2}{2m_1}v_2\Delta t, \] \[\Delta s\,=\, \frac {240+160}{2{\cdot}240}\cdot0{,}9{\cdot}1{,}5\,\mathrm{m},\] \[\Delta s\,=\, 1{,}1\,\mathrm{m}.\]
Situaci můžeme také řešit v soustavě spojené například s první loďkou.

V této soustavě se druhá loďka vzdaluje rovnoměrně zrychleným pohybem a za dobu Δt dosáhne konečné rychlosti o velikosti v. Změna vzdálenosti je:
\[\Delta s\,=\,\frac{1}{2}v\Delta t,\]
\(\Delta s\)…změna vzdálenosti druhé loďky od první.

Za rychlost v dosadíme ze vztahu (2):
\[\Delta s\,=\, \frac {m_1+m_2}{2m_1}v_2\Delta t.\tag{3}\]
Odpověď: Změna vzdálenosti loděk během silového působení chlapce na první loďce je \(\Delta s\,=\, 1{,}1\,\mathrm{m}.\)
Celkové řešení bodu d)
Práce vykonaná během odstrkování loděk se projeví vzrůstem kinetické energie obou loděk. (Změny vnitřní energie neuvažujeme.)
\[W\,=\,E_\mathrm{k1}+E_\mathrm{k2}\]
\(W\)…vykonaná práce

\(E_\mathrm{k1}\)…kinetická energie první loďky s chlapcem

\(E_\mathrm{k2}\)…kinetická energie druhé loďky s chlapcem
\[W\,=\,\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\]
Za rychlost v₁ dosadíme ze vztahu (1):
\[W\,=\,\frac{1}{2}m_1\frac{m_2^2v_2^2}{m_1^2}+\frac{1}{2}m_2v_2^2,\] \[W\,=\,\frac{m_2^2v_2^2}{2m_1}+\frac{m_2v_2^2}{2},\] \[W\,=\,\frac{m_2(m_1+m_2)}{2m_1}v_2^2,\] \[W\,=\,\frac{160\cdot(240+160)}{2{\cdot}240}\cdot0{,}9^2\,\mathrm{J},\] \[W\,=\,108\,\mathrm{J}.\]
Odpověď: Práce vykonaná během odstrkování loděk je rovna \(W\,=\,108\,\mathrm{J}.\)
Celkové řešení bodu e)
Poměr kinetické energie druhé loďky E_k2 ke kinetické energii první loďky E_k1 je:
\[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{\frac{1}{2}m_2v_2^2}{\frac{1}{2}m_1v_1^2},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{m_2v_2^2}{m_1\frac{m_2^2v_2^2}{m_1^2}},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{m_1}{m_2},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{240}{160},\] \[\frac{E_\mathrm{k2}}{E_\mathrm{k1}}\,=\,\frac{3}{2}.\]
Odpověď: Poměr kinetických energií druhé a první loďky je \(\frac{E_{k2}}{E_{k1}}\,=\,\frac{3}{2}\).