Kamínek na římse
Úloha číslo: 127
Kamínek sklouzne z římsy, která je ve výšce h nad povrchem země, a volně padá k zemi. Rozdělte výšku h na n částí tak, aby čas pádu kamínku byl v každé z nich stejný.
Zanedbejte odpor vzduchu.
Řešte pro hodnoty: h = 245 m, n = 5.
Nápověda 1: Označení
Označte si jednotlivé části, na které budete výšku h dělit, a označte si také čas pádu v jednotlivých částech, který bude pro všechny stejný.
Nápověda 2: Dráha pohybu
Jednotlivé části můžete považovat za dílčí dráhy, které kamínek uletěl při volném pádu z římsy dolů. Čemu je roven jejich součet?
Jaký vztah platí mezi dráhou volného pádu a dobou pádu? Napište ho nejprve pro první úsek, pak pro první dva úseky a pak obecně pro n úseků.
Nápověda 3: Doba pádu
Ze vztahu (3) z minulé nápovědy snadno vyjádříte dobu pádu t0 pro každou jednotlivou část (je pro všechny části stejná).
Nápověda 4: Rozdělení výšky pádu na části
Využijte vztah (4) pro dobu pádu z minulé nápovědy a vyjádřete jednotlivé úseky pádu xi pomocí výšky pádu h a počtu částí n.
CELKOVÉ ŘEŠENÍ
Jednotlivé části pádu kamínku si označíme: \(x_1, x_2,..., x_\mathrm{n}.\)
Čas pádu, stejný pro všechny části, označíme t0.
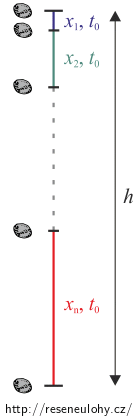
Jednotlivé části můžeme považovat za dílčí dráhy, které kamínek uletěl při volném pádu z římsy dolů.
Pro jejich součet platí: \(h=x_1+x_2+...+x_\mathrm{n}\).
Platí:
\[x_1=\frac{gt_0^{2}}{2}\,,\tag{1}\] \[x_1+x_2=\frac{g(2t_0)^{2}}{2}\,,\tag{2}\] \[h=x_1+x_2+...+x_n=\frac{g(nt_0)^{2}}{2}\,.\tag{3}\]Doba pádu t0 pro každou jednotlivou část vyjádřená ze vztahu (3) je:
\[t_0^{2}=\frac{2h}{g}\frac{1}{n^{2}}\,.\tag{4}\]Dosadíme za t0 do vztahu (1) pro 1. úsek dráhy:
\[x_1=\frac{gt_0^{2}}{2}=\frac{h}{n^{2}}\,.\]Druhý úsek dráhy vyjádříme ze vztahu (2) a opět dosadíme za t0:
\[x_2=\frac{g(2t_0)^{2}}{2}-x_1=h\left(\frac{2}{n}\right)^{2}-h\left(\frac{1}{n}\right)^{2}=\frac{3h}{n^{2}}\,.\]Pro i-tý úsek dráhy bude platit:
\[x_\mathrm{i}=\frac{1}{2}g(it_0)^{2}-\frac{1}{2}g[(i-1)t_0]^{2}=\frac{gt_0^{2}}{2}(2i-1)=\frac{g}{2}.\frac{2h}{g}.\frac{1}{n^{2}}(2i-1)\,,\] \[x_\mathrm{i}=\frac{2i-1}{n^{2}}h\,.\]Číselně:
pro: \(i=1{,}2,...,5\), \(h=245\,\mathrm{m} \), \(n=5\) dostaneme:
\[x_1=\frac{245}{25}\,\mathrm{m}=9{,}8\,\mathrm{m}\,,\] \[x_2=\frac{3.245}{25}\,\mathrm{m}=29{,}4\,\mathrm{m}\,,\] \[x_3=\frac{5.245}{25}\,\mathrm{m}=49{,}0\,\mathrm{m}\,,\] \[x_4=\frac{7.245}{25}\,\mathrm{m}=68{,}6\,\mathrm{m}\,,\] \[x_5=\frac{9.245}{25}\,\mathrm{m}=88{,}2\,\mathrm{m}\,.\]Odpověď
Pro jednotlivé úseky pádu kamínku z římsy platí:
\[x_1=\frac{h}{n^{2}}\,,\] \[x_2=\frac{3h}{n^{2}}\,,\] \[x_\mathrm{i}=\frac{2i-1}{n^{2}}h\,.\]Pro \(i=1{,}2,...,5\); \(h=245\,\mathrm{m} \); \(n=5\) dostaneme:
\[x_1=9{,}8\,\mathrm{m}\,,\] \[x_2=29{,}4\,\mathrm{m}\,,\] \[x_3=49{,}0\,\mathrm{m}\,,\] \[x_4=68{,}6\,\mathrm{m}\,,\] \[x_5=88{,}2\,\mathrm{m}\,.\]




