Nákladní auto a kopec
Úloha číslo: 215
Nákladní auto jede stálou rychlostí 30 km·h−1 z kopce. Hmotnost auta je 5 t. Auto brzdí pomocí motoru, celková brzdná síla působící na auto má velikost 4400 N. Určete sklon kopce.
Zápis
m = 5 t hmotnost auta Fb = 4400 N brzdná síla v = 30 km·h−1 rychlost auta α = ? (°) sklon kopce Nápověda 1
Jaké síly na auto během pohybu působí? Jaký mají směr? Nakreslete si obrázek.
Nápověda 2
Co platí podle 1. Newtonova zákona pro výslednici těchto sil?
Nápověda 3
Rozložte tíhovou sílu \(\vec{F}_\mathrm{G}\) na složku rovnoběžnou s vozovkou a na složku kolmou k vozovce. Dává 1. Newtonův zákon nějaké podmínky pro tyto složky?
Nápověda 4
Umíte vyjádřit velikost složky F0 z tíhové síly? Použijte vhodnou goniometrickou funkci a pomocí známé velikosti brzdné síly Fb vyjádřete z rovnice (4) úhel α.
Celkové řešení
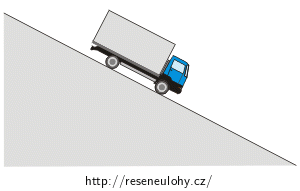
Na auto působí celkem tři síly:
1) Tíhová síla \(\vec{F}_\mathrm{G}\) působí svisle dolů.
2) Reakční síla vozovky \(\vec{R}\) (auto tlačí do vozovky a podle 3. Newtonova zákona tlačí vozovka do auta). Tato síla působí kolmo na vozovku.
3) Brzdná síla \(\vec{F}_\mathrm{b}\), která působí proti směru pohybu.
Protože automobil se pohybuje rovnoměrně přímočaře, musí být výslednice tří výše zmíněných sil nulová (nulový vektor):
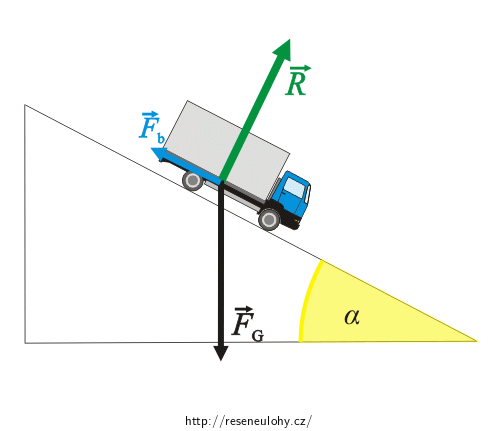
\[\vec{F}_\mathrm{G} \,+\,\vec{R}\,+\,\vec{F}_\mathrm{b}\,=\,\vec{o}.\]Tíhovou sílu \(\vec{F}_\mathrm{G}\) můžeme rozložit na sílu \(\vec{F}_0\) rovnoběžnou s vozovkou a na sílu \(\vec{F}_\mathrm{n}\) kolmou k vozovce. Tento rozklad ukazuje další obrázek:
Z něj je také patrné, že má-li být výslednice všech sil působících na automobil nulová, musí být nulové také výslednice ve směru rovnoběžném s vozovkou a ve směru kolmém k vozovce. Musí tedy platit:
\[\vec{F}_\mathrm{n}\,+\,\vec{R}\,=\,\vec{o},\tag{1}\] \[\vec{F}_0\,+\,\vec{F}_\mathrm{b}\,=\,\vec{o}.\tag{2}\]Protože síly \(\vec{F}_\mathrm{n}\) a \(\vec{R}\) mají opačný směr a síly \(\vec{F}_0\) a \(\vec{F}_\mathrm{b}\) mají také opačný směr, lze pro velikosti těchto sil psát:
\[F_\mathrm{n}\,-\,R\,=\,0,\tag{3}\] \[F_0\,-\,F_\mathrm{b}\,=\,0.\tag{4}\]Pro další výpočet nám postačí pracovat s rovnicí (4).
Z geometrie úlohy (viz obrázek výše) je patrné, že platí:
\[\sin{\alpha}\,=\,\frac{F_0}{F_\mathrm{G}}.\]Tedy:
\[F_0\,=\,F_\mathrm{G}\sin{\alpha}.\tag{5}\]Tíhovou sílu FG můžeme pomocí hmotnosti automobilu vyjádřit jako:
\[F_\mathrm{G}\,=\,mg\,,\tag{6}\]kde g je tíhové zrychlení. Dosazením vztahu (6) do vztahu (5) dostáváme:
\[F_0\,=\,mg\sin{\alpha}.\tag{7}\]Konečně kombinací vztahů (4) a (7) získáváme výslednou rovnost:
\[ mg\sin{\alpha}\,-\,F_\mathrm{b}\,=\,0\,\Rightarrow\,\sin{\alpha}\,=\,\frac{F_\mathrm{b}}{mg}.\]Číselně:
\[F_\mathrm{b}\,=\,4400\,\mathrm{N},\] \[m\,=\,5\,\mathrm{t}\,=\,5000\,\mathrm{kg},\] \[g\,=\,9{,}81\,\mathrm{m{\cdot}s^{-2}},\] \[\sin{\alpha}\,=\,\frac{F_b}{mg}\,=\,(\frac{4400}{5000{\cdot}9{,}81})\,\dot{=}\,0{,}090\,\Rightarrow\,\alpha\,\dot{=}\,5^{\circ}8^{\prime}.\]Kopec klesá pod úhlem \(5^{\circ}8^{\prime}\), přepočítáno na procenta vyjde klesání přibližně \(9\,\%.\) (Klesáním (stoupáním) se rozumí hodnota tangenty úhlu přepočtená na procenta.)
Povšimněte si, že sklon kopce nezávisí na rychlosti, kterou má automobil „udržet“, ale pouze na brzdné síle, která je k tomu zapotřebí.
Výsledek
\[\sin{\alpha}\,=\,\frac{F_b}{mg}\,=\,0{,}090\,\Rightarrow\,\alpha\,=\,5^{\circ}8^{\prime}\]Kopec klesá pod úhlem přibližně \(5^{\circ}8^{\prime}\), resp. přibližně \(9\,\%\).




