Zvedání duté bedny
Úloha číslo: 1144
Krychlová bedna o hraně 1 metr, která má stěny z materiálu o hustotě 2000 kg/m3 tlusté 25 cm, je uvnitř naplněná vzduchem (jehož hmotnost zanedbáme) a leží na dně nádrže s vodou hluboké 12 m. Určete:
- Jakou práci vykonal jeřáb, když vytáhl bednu tak, že se její vrchní stěna dotkla hladiny?
- Jakou práci by vykonal, kdyby byla bedna naplněna nikoli vzduchem, ale vodou?
- Jakou hustotu by musela mít kapalina, kterou bychom bednu naplnili, aby práce jeřábu byla dvakrát větší, než když byla bedna naplněna vzduchem?
Zápis
a = 1 m délka hrany bedny d = 25 cm tloušťka stěn bedny ρ = 2000 kg/m3 hustota materiálu stěn h = 12 m hloubka nádrže W1 = ? práce jeřábu v případě a) W2 = ? práce jeřábu v případě b) ρ2 = ? hustota kapaliny v případě c) Nápověda 1 (k části a.)
Jaké síly působí na bednu v libovolném okamžiku, když je zvedána (předpokládejme, že rovnoměrně) ze dna k hladině? Určete výslednici těchto sil. Vztah poté přepište skalárně a obecně z něj vyjádřete sílu, kterou musí jeřáb bednu zvedat.
Nápověda 2 (k části a.)
Vyjádřete tíhovou sílu působící na bednu. Nejste-li si jisti objemem stěn bedny, udělejte si obrázek. Využijete také vztah mezi objemem, hmotností a hustotou.
Nápověda 3 (k části a.)
Určete vztlakovou sílu působící na bednu. Nezapomeňte, že nyní pracujete s ponořeným objemem tělesa.
Nápověda 4 (k části a.)
Dosaďte velikosti tíhové a vztlakové síly do vztahu (2). Jak nyní s pomocí tažné síly jeřábu určit jeho práci? Vzpomeňte si na definiční vztah pro mechanickou práci a první část úlohy dopočítejte.
Nápověda 5 (k části b.)
Jak se situace změní, naplníme-li dutinu uvnitř bedny vodou? Změní se tíhová síla působící na bednu? Změní se vztlaková síla působící na bednu? Práci vypočítejte stejným způsonem jako v části a).
Nápověda 6 (k části c.)
Poslední část úlohy je velmi podobná té předcházející, pouze bednu plníme kapalinou s jinou hustotou. Vyjádřete práci W3, která je potřebná na vyzvednutí bedny naplněné neznámou kapalinou (využijte přitom zobecnění okomentovaného u vztahu(14)). Pak už pouze přidejte podmínku, že práce W3 má být dvojnásobkem práce W1, a vyjádřete neznámou hustotu.Celkové řešení
Část a:
Je-li bedna zvedána k hladině, působí na ni tyto síly:
- tíhová síla FG směrem svisle dolů
- vztlaková síla Fvz směrem svisle vzhůru
- tažná síla jeřábu F směrem svisle vzhůru
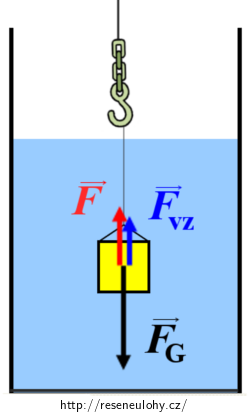
Protože tento pohyb je dle našeho předpokladu rovnoměrný přímočarý, musí být podle 1. Newtonova zákona výslednice těchto sil nulová:
\[\vec{F_\mathrm{G}}\,+\,\vec{F_\mathrm{vz}}\,+\,\vec{F}\,=\,\vec{o}\tag{1}\]Vzhledem ke směru jednotlivých sil (viz výše) můžeme přepsat rovnici (1) skalárně a vyjádřit z ní velikost tažné síly jeřábu F:
\[F_\mathrm{G}\,-\,F_\mathrm{vz}\,-\,F\,=\,0\,\Rightarrow\,F\,=\,F_\mathrm{G}\,-\,F_\mathrm{vz}.\tag{2}\]Výpočet tíhové síly: Tíhovou sílu spočítáme dle vztahu:
\[F_\mathrm{G}\,=\,mg,\tag{3}\]kde m je hmotnost bedny a g tíhové zrychlení. Protože máme zadanou hustotu materiálu ρ, ze kterého je bedna vyrobena, můžeme hmotnost ve vztahu (3) rozepsat jako součin objemu a hustoty:
\[F_\mathrm{G}\,=\,{\rho}Vg,\tag{4}\]kde V je objem stěn bedny (nikoli vnější objem celé bedny, bedna je dutá!). Při určení tohoto objemu si pomůžeme obrázkem:
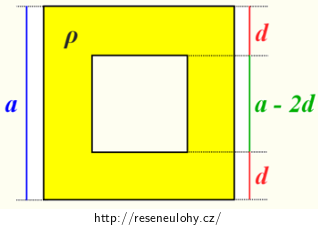
Bednu si tedy můžeme představit jako krychli o hraně a, ve které je dutina ve tvaru krychle o hraně a −2d. Z toho by mělo být patrné, že objem stěn je roven rozdílu mezi objemem V1 velké krychle a objemem V2 malé (vnitřní) krychle. S pomocí vztahu pro objem krychle dostáváme:
\[V\,=\,V_1\,-\,V_2\,=\,a^3\,-\,(a\,-\,2d)^3\,=\,2d(3a^2\,-\,6ad\,+\,4d^2).\tag{5}\]Dosazením vztahu (5) do rovnice (4) dostáváme pro tíhovou sílu:
\[F_\mathrm{G}\,=\,2{\rho}gd(3a^2\,-\,6ad\,+\,4d^2).\tag{6}\]Výpočet vztlakové síly: Ve vztahu pro velikost vztlakové síly Fvz vystupuje kromě tíhového zrychlení g a hustoty kapaliny (zde vody) ρ1 také objem ponořené části tělesa, tedy náš „vnější“ objem V1. Dutina uvnitř bedny se na tomto objemu nijak neprojeví. Bude tedy platit:
\[F_\mathrm{vz}\,=\,V_1{\rho}_1g\,=\,a^3{\rho}_1g.\tag{7}\]Výpočet tažné síly: Dosazením vztahů (6) a (7) získáváme tažnou sílu jeřábu F:
\[F\,=\,g(2{\rho}d(3a^2\,-\,6ad\,+\,4d^2)\,-\,a^3{\rho}_1).\tag{8}\]Z definice víme, že mechanickou práci určíme jako součin konstantní síly a dráhy, na které tato síla působila. Sílu jsme určili ve vztahu (8), pro dráhu s z obrázku platí:
\[s\,=\,h\,-\,a.\tag{9}\]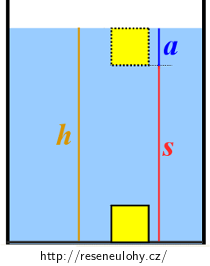
Ve výsledku tedy pro hledanou práci jeřábu dostáváme:
\[W_1\,=\,Fs\,=\,g(h\,-\,a)(2{\rho}d(3a^2\,-\,6ad\,+\,4d^2)\,-\,a^3{\rho}_1).\tag{10}\]Číselně:
\[W_1\,=\,10(12\,-\,1)(2{\cdot}2\,000{\cdot}0{,}25{\cdot}(3{\cdot}1^2\,-\,6{\cdot}1{\cdot}0{,}25\,+\,4{\cdot}0{,}25^2)\,-\,1^3{\cdot}1\,000)\,\mathrm{J}\] \[W_1\,=\,82\,500\mathrm{J}.\]Jeřáb vykoná při zvedání bedny k hladině práci 82,5 kJ.
Část b:
Abychom mohli vyřešit druhou část úlohy, musíme nejprve prozkoumat, jak vyplnění dutiny vodou změní silové poměry („nové“ síly budeme značit čárkovaně):
Tíhová síla: Vyplníme-li dutinu bedny vodou, zvýší se hmotnost celého tělesa o hmotnost dolité vody m1 a vzroste tedy tíhová síla působící na bednu:
\[F_\mathrm{G}´\,=\,F_\mathrm{G}\,+\,m_1g\,=\,F_\mathrm{G}\,+\,{\rho}_1gV_2\,=\,F_\mathrm{G}\,+\,{\rho}_1g(a\,-\,2d)^3,\tag{11}\]kde V2 je již dříve spočítaný objem dutiny (a tedy i nalité vody) a ρ1 hustota vody.
Vztlaková síla: Vnější objem bedny se nezmění a vztlaková síla tak zůstane stejně velká:
\[F_\mathrm{vz}´\,=\,F_\mathrm{vz}.\tag{12}\]Pro výslednou tažnou sílu jeřábu F´ obměnou vztahu (2) platí:
\[F´\,=\,F_\mathrm{G}´\,-\,F_\mathrm{vz}´\,=\,(F_\mathrm{G}\,-\,F_\mathrm{vz})\,+\,{\rho}_1g(a\,-\,2d)^3,\] \[F´\,=\,F\,+\,{\rho}_1g(a\,-\,2d)^3.\tag{13}\]Práci W2 určíme analogicky jako ve vztahu (10):
\[W_2\,=\,F´s\,=\,F´(h\,-\,a)\,=\,F(h\,-\,a)\,+\,{\rho}_1g(a\,-\,2d)^3(h\,-\,a),\] \[W_2\,=\,W_1\,+\,{\rho}_1g(a\,-\,2d)^3(h\,-\,a).\tag{14}\]Z tvaru výsledku vidíme, že celková práce vykonaná při zvednutí bedny naplněné vodou je rovna součtu práce vykonané při zvednutí prázdné bedny (W1) a práce vykonané při zvedání samotné vody (výraz ve vztahu (14) vpravo). Číselně:
\[W_2\,=\,(82\,500\,+\,1000{\cdot}10{\cdot}(1\,-\,2{\cdot}0{,}25)^3{\cdot}(12\,-\,1))\,\mathrm{J}\,=\,96\,250\,\mathrm{J}.\]Část c:
K určení práce W3, potřebné k vyzvednutí bedny s neznámou kapalinou, využijeme zobecnění dané vztahem (14). V něm jsme odvodili, že práci na vyzvednutí plné bedny lze vyjádřit jako součet práce na vyzvednutí prázdné bedny a práce na vyzvednutí jejího obsahu. Oproti situaci popsané vztahem (14) se změnila pouze jediná veličina – hustota kapaliny v bedně; proto lze vztah (14) téměř identicky přepsat pro práci W3:
\[W_3\,=\,W_1\,+\,{\rho}_2g(a\,-\,2d)^3(h\,-\,a),\tag{15}\]kde ρ2 je hustota neznámé kapaliny. Z podmínky dané zadáním úlohy ale současně platí:
\[W_3\,=\,2W_1.\tag{16}\]Porovnáním vztahů (15) a (16) dostáváme:
\[W_1\,+\,{\rho}_2g(a\,-\,2d)^3(h\,-\,a)\,=\,2W_1.\]Odtud úpravou:
\[W_1\,=\,{\rho}_2g(a\,-\,2d)^3(h\,-\,a)\,\Rightarrow\,{\rho}_2\,=\,\frac{W_1}{g(a\,-\,2d)^3(h\,-\,a)}.\tag{17}\]Číselně:
\[{\rho}_2\,=\,\frac{82\,500}{10{\cdot}(1\,-\,2{\cdot}0{,}25)^3{\cdot}(12\,-\,1)}\,\mathrm{kg}{\cdot}\mathrm{m}^{-3}\,=\,6\,000\,\mathrm{kg}{\cdot}\mathrm{m}^{-3}.\]Odpověď
Část a: Jeřáb musí působit tažnou silou 82,5 kJ.
Část b: Jeřáb by musel působit tažnou silou 96,25 kJ.
Část c: Hustota kapaliny v dutině bedny by musela být 6000 kg·m−3.


