Částice α
Úloha číslo: 151
Částice α se srazí s jádrem atomu kyslíku, které bylo před srážkou v klidu. Její výsledná rychlost svírá s původním směrem jejího pohybu úhel 64,0°. Kyslíkové jádro se po srážce pohybuje rychlostí o velikosti 1,20·105 m s-1, která svírá s původním směrem pohybu α-částice úhel -51,0°. (Hmotnost α-částice je 4,0u a hmotnost kyslíkového jádra 16,0u.)
a) Určete velikost výsledné rychlosti α-částice.
b) Určete velikost počáteční rychlosti α-částice.
Zápis
m1 = 4u hmotnost α-částice m2 = 16u hmotnost kyslíkového jádra v'2 = 1,2·105 m·s-1 rychlost kyslíkového jádra po srážce α1 = 64° úhel mezi výslednou rychlostí α-částice a jejím původním směrem α2 = 51° úhel mezi výslednou rychlostí kyslíkového jádra a jeho původním směrem v'1 = ? (m·s-1) velikost výsledné rychlosti α-částice v1 = ? (m·s-1) velikost počáteční rychlosti α-částice Nápověda 1 - zákon zachování hybnosti
Nakreslete si obrázek. Jaký zákon platí pro hybnost soustavy před srážkou a po srážce?
Nápověda 2 - Skalární přepis ZZH
Zvolte vhodně soustavu souřadnic a přepište vztah (1) skalárně. Ze získaných rovnic vyjádřete hledané rychlosti.
Číselný výpočet
Dáno:
\[m_1\,=\,4\mathrm{u},\] \[m_2\,=\,16\mathrm{u},\] \[v_2{'}\,=\,1{,}2{\cdot}10^5\,\mathrm{m \cdot s^{-1}},\] \[\alpha_1\,=\,64^{\circ},\] \[\alpha_2\,=\,51^{\circ}.\]Hledáme:
a) \[v_1{'}\,=\,?,\] \[v_1{'}\,=\,\frac{m_2v_2{'}\sin \alpha_2}{m_1\sin \alpha_1},\] \[v_1{'}\,=\,\frac{16u\cdot1{,}2{\cdot}10^5\cdot\sin 51^{\circ}}{4u\cdot\sin64^{\circ}}\,\mathrm{m \cdot s^{-1}},\] \[v_1{'}\,=\,4{,}15{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\] b) \[v_1\,=\,?,\] \[v_1\,=\,\frac{m_2v_2{'}\sin \alpha_2\cos \alpha_1}{m_1\sin \alpha_1}+\frac {m_2v_2{'}\cos \alpha_2}{m_1},\] \[v_1\,=\,(\frac{16u\cdot1{,}2{\cdot}10^5\cdot\sin 51^{\circ}cos 64^{\circ}}{4u\cdot\sin 64^{\circ}}+\frac {16u\cdot1{,}2{\cdot}10^5\cdot\cos 51^{\circ}}{4u})\,\mathrm{m \cdot s^{-1}},\] \[v_1\,=\,(1{,}82+3{,}02)\cdot10^5\,\mathrm{m \cdot s^{-1}},\] \[v_1\,=\,4{,}84{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\]Odpověď
a) Velikost výsledné rychlosti částice α je \[v_1{'}\,=\,\frac{m_2v_2{'}\sin \alpha_2}{m_1\sin \alpha_1}\,=\,4{,}15{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\]
b) Velikost počáteční rychlosti částice α je \[v_1\,=\,\frac{m_2v_2{'}\sin \alpha_2\cos \alpha_1}{m_1\sin \alpha_1}+\frac {m_2v_2{'}\cos \alpha_2}{m_1}\,=\,4{,}84{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\]
Celkové řešení
Nakreslíme obrázek situace:
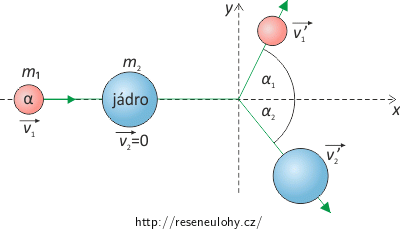
Při srážce se hybnost soustavy zachovává čili platí zákon zachování hybnosti (ZZH):
\[\mathrm{ZZH:}\qquad \vec {p_1}+\vec{p_2}\,=\,\vec{p_1^{'}}+\vec{p_2^{'}}.\]\(\vec{p_1}\)…vektor hybnosti částice α před srážkou
\(\vec{p_2}\)…vektor hybnosti jádra atomu kyslíku před srážkou
\(\vec{p_1^{'}}\)…vektor hybnosti částice α po srážce
\(\vec{p_2^{'}}\)…vektor hybnosti jádra atomu kyslíku po srážce
\[m_1\vec {v_1}+m_2\vec {v_2}\,=\,m_1\vec{v_1^{'}}+m_2\vec{v_2^{'}}\]\(m_1\)…hmotnost částice α
\(m_2\)…hmotnost jádra atomu kyslíku
\(\vec{v_1}\)…vektor rychlosti částice α před srážkou
\(\vec{v_2}\)…vektor rychlosti jádra atomu kyslíku před srážkou
\(\vec{v_1^{'}}\)…vektor rychlosti částice α po srážce
\(\vec{v_2^{'}}\)…vektor rychlosti jádra atomu kyslíku po srážce
Víme, že jádro atomu kyslíku je před srážkou v klidu, \(v_2\,=\,0\):
\[m_1\vec {v_1}+0\,=\,m_1\vec{v_1^{'}}+m_2\vec{v_2^{'}}.\tag{1}\]Souřadný systém zvolíme tak, že osu x orientujeme ve směru původního pohybu částice α. Osu y pak kolmo na ni (viz obrázek). Vztah (1) přepíšeme skalárně:
x-ová složka:
\[m_1v_1\,=\,m_1v_1^{'}\cos \alpha_1+m_2v_2^{'}\cos \alpha_2,\tag{2}\]y-ová složka:
\[0\,=\,m_1v_1^{'}\sin \alpha_1-m_2v_2^{'}\sin \alpha_2,\tag{3}\]\(\alpha_1\)…úhel, který svírá výsledná rychlost částice α s původním směrem,
\(\alpha_2\)…úhel, který svírá výsledná rychlost jádra atomu kyslíku s původním směrem částice α.
Ze vztahu (3) si vyjádříme výslednou rychlost částice α:
\[v_1{'}\,=\,\frac{m_2v_2^{'}\sin \alpha_2}{m_1\sin \alpha_1},\] \[v_1{'}\,=\,\frac{16u\cdot1{,}2{\cdot}10^5\cdot\sin 51^{\circ}}{4u\cdot\sin64^{\circ}}\,\mathrm{m \cdot s^{-1}},\] \[v_1{'}\,=\,4{,}15{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\]Dosadíme do vztahu (2):
\[m_1v_1\,=\,m_1\frac{m_2v_2^{'}\sin \alpha_2}{m_1\sin \alpha_1}\cos \alpha_1+m_2v_2^{'}\cos \alpha_2.\]Vydělíme hmotností m1:
\[v_1\,=\,\frac{m_2v_2^{'}\sin \alpha_2\cos \alpha_1}{m_1\sin \alpha_1}+\frac {m_2v_2^{'}\cos \alpha_2}{m_1},\] \[v_1\,=\,(\frac{16u\cdot1{,}2{\cdot}10^5\cdot\sin 51^{\circ}cos 64^{\circ}}{4u\cdot\sin 64^{\circ}}+\frac {16u\cdot1{,}2{\cdot}10^5\cdot\cos 51^{\circ}}{4u})\,\mathrm{m \cdot s^{-1}},\] \[v_1\,=\,(1{,}82+3{,}02)\cdot10^5\,\mathrm{m \cdot s^{-1}},\] \[v_1\,=\,4{,}84{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\]Odpověď:
a) Velikost výsledné rychlosti částice α je \[v_1{'}\,=\,\frac{m_2v_2^{'}\sin \alpha_2}{m_1\sin \alpha_1}\,=\,4{,}15{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\]
b) Velikost počáteční rychlosti částice α je \[v_1\,=\,\frac{m_2v_2^{'}\sin \alpha_2\cos \alpha_1}{m_1\sin \alpha_1}+\frac {m_2v_2^{'}\cos \alpha_2}{m_1}\,=\,4{,}84{\cdot}10^5\,\mathrm{m \cdot s^{-1}}.\]




