Sbírka řešených úloh

Mars v opozici se Sluncem

Úloha číslo: 1238

V roce 1672, když se nacházel Mars nejblíže Zemi (viz obrázek k zadání), astronomové zjistili, že vzdálenost Marsu a Země je \(73{\cdot}10^6 \mathrm{km}\). Dále znali oběžnou dobu Země \((365  \mathrm{d})\) a Marsu \((687  \mathrm{d})\) kolem Slunce a Keplerovy zákony. To jim umožnilo vypočítat do té doby neznámou vzdálenost Země a Slunce.

Jaká vzdálenost jim vyšla? Jak moc se liší od hodnoty, kterou známe dnes?

Poznámka: Trajektorie planet považujte za kružnice.

• Zápis

  \(d=73{\cdot}10^6 \mathrm{km}\)	vzdálenost Marsu a Země
  \(T_\mathrm{Z}=365 \mathrm{d}\)	oběžná doba Země
  \(T_\mathrm{M}=687 \mathrm{d}\)	oběžná doba Marsu
  \(r_\mathrm{Z}= ?\)	vzdálenost Země od Slunce

• Rozbor

  Zamysleme se, který z Keplerových zákonů pomohl astronomům spočítat hledanou vzdálenost Země a Slunce.

  Známe oběžné doby Země a Marsu kolem Slunce. Poloměr trajektorie Marsu umíme vyjádřit pomocí známé vzdálenosti Země a Marsu a hledaného poloměru trajektorie Země.

  Oběžné doby planet a délky hlavních poloos jejich trajektorií (my je považujeme za kružnice) dává do souvislosti 3. Keplerův zákon. Zapíšeme-li ho, získáme rovnici, ze které již dokážeme vyjádřit hledanou vzdálenost Země a Slunce.

• Nápověda 1

  Nakreslete obrázek se Sluncem, Zemí a Marsem. Zakreslete do něj kruhové trajektorie Země a Marsu. Vyznačte v něm poloměr trajektorie Země \(r_\mathrm{Z}\), poloměr trajektorie Marsu \(r_\mathrm{M}\) a vzdálenost Země a Marsu \(d\).

• Řešení nápovědy 1

  

• Nápověda 2

  Na základě obrázku (trajektorie) napište, jaký je vztah mezi \(r_\mathrm{M}\), \(r_\mathrm{Z}\) a \(d\).

• Řešení nápovědy 2

  Bude platit: \[r_\mathrm{M}=r_\mathrm{Z}+d.\tag{1}\]

• Nápověda 3

  Formulujte třetí Keplerův zákon pro Zemi a Mars.

• Řešení nápovědy 3

  Třetí Keplerův zákon: Poměr druhých mocnin oběžných dob dvou planet se rovná poměru třetích mocnin délek hlavních poloos jejich trajektorií.

  V našem případě bude platit: \[\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}=\frac{r_\mathrm{Z}^3}{r_\mathrm{M}^3}.\tag{2}\]

• Nápověda 4

  Do (2) dosaďte dle (1) za \(r_\mathrm{M}\) a vyjádřete \(r_\mathrm{Z}\). Dopočítejte číselně.

• Řešení nápovědy 4

  Dosadíme (1) do (2): \[\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}=\frac{r_\mathrm{Z}^3}{\left(r_\mathrm{Z}+d \right)^3}.\]

  Obě strany rovnice odmocníme třetí odmocninou: \[\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}=\frac{r_\mathrm{Z}}{r_\mathrm{Z}+d }.\] Nejprve obě strany rovnice vynásobíme \(r_\mathrm{Z}+d\) a poté od obou stran rovnice odečteme \(r_\mathrm{Z}\): \[ \sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}r_\mathrm{Z}+\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d-r_\mathrm{Z}=0.\] Od obou stran rovnice odečteme člen \(\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d\) a na levé straně rovnice vytkneme \(-r_\mathrm{Z}\): \[ -r_\mathrm{Z}\left(1-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}\right)=-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d.\] Obě strany rovnice vydělíme \(-\left(1-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}} \right)\) a dostáváme: \[r_\mathrm{Z}=\frac{\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d}{1-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}}.\]

  Číselné řešení:

  Ze zadání víme, že \(d=73{\cdot}10^6 \mathrm{km}\), \(T_\mathrm{Z}=365 \mathrm{d}\) a \(T_\mathrm{M}=687 \mathrm{d}\).

  \[r_\mathrm{Z}=\frac{\sqrt[3]{\frac{365^2}{687^2}}\cdot73{\cdot}10^6}{1-\sqrt[3]{\frac{365^2}{687^2}}} \mathrm{km} \dot= \frac{47{,}89}{0{,}34}\cdot10^6 \mathrm{km} \dot= 140{\cdot}10^6 \mathrm{km}.\]

• Celkové řešení

  Obrázek trajektorie Země a Marsu

   

  

   

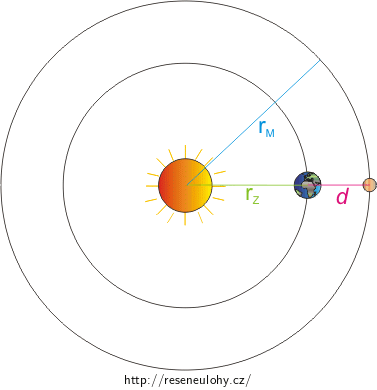
  Vztah mezi \(r_\mathrm{M}\), \(r_\mathrm{Z}\) a \(d\)

   

  Bude platit: \[r_\mathrm{M}=r_\mathrm{Z}+d.\tag{1}\]

   

  Třetí Keplerův zákon pro Zemi a Mars

   

  Poměr druhých mocnin oběžných dob dvou planet se rovná poměru třetích mocnin délek hlavních poloos jejich trajektorií.

  V našem případě bude platit: \[\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}=\frac{r_\mathrm{Z}^3}{r_\mathrm{M}^3}.\tag{2}\]

   

  Vyjádření \(r_\mathrm{Z}\)

   

  Dosadíme dle (1) za \(r_\mathrm{M}\) do (2): \[\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}=\frac{r_\mathrm{Z}^3}{\left(r_\mathrm{Z}+d \right)^3}.\]

  Obě strany rovnice odmocníme třetí odmocninou: \[\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}=\frac{r_\mathrm{Z}}{r_\mathrm{Z}+d }.\] Nejprve obě strany rovnice vynásobíme \(r_\mathrm{Z}+d\) a poté od obou stran rovnice odečteme \(r_\mathrm{Z}\): \[ \sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}r_\mathrm{Z}+\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d-r_\mathrm{Z}=0.\] Od obou stran rovnice odečteme člen \(\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d\) a na levé straně rovnice vytkneme \(-r_\mathrm{Z}\): \[ -r_\mathrm{Z}\left(1-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}\right)=-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d.\] Obě strany rovnice vydělíme \(-\left(1-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}} \right)\) a dostáváme: \[r_\mathrm{Z}=\frac{\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d}{1-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}}.\]

  Číselné řešení:

  Ze zadání víme, že \(d=73{\cdot}10^6 \mathrm{km}\), \(T_\mathrm{Z}=365 \mathrm{d}\) a \(T_\mathrm{M}=687 \mathrm{d}\).

  \[r_\mathrm{Z}=\frac{\sqrt[3]{\frac{365^2}{687^2}}\cdot73{\cdot}10^6}{1-\sqrt[3]{\frac{365^2}{687^2}}} \mathrm{km} \dot= \frac{47{,}89}{0{,}34}\cdot10^6 \mathrm{km} \dot= 140{\cdot}10^6 \mathrm{km}.\]

• Odpověď

  Vzdálenost Země a Slunce jim vyšla \(r_\mathrm{Z}=\frac{\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}d}{1-\sqrt[3]{\frac{T_\mathrm{Z}^2}{T_\mathrm{M}^2}}}\), což je číselně přibližně \(140{\cdot}10^6 \mathrm{km}\). Průměrná hodnota vzdálenosti, kterou známe dnes, je \(149{,}6{\cdot}10^6 \mathrm{km} \). Hodnota vypočítaná astronomy v roce 1672 je dobrým přiblížením dnešní hodnotě.