Zdviž
Úloha číslo: 86
Kabina plně naložené zdviže má hmotnost 1200 kg. Kabinu je třeba zvednout do výšky 54 m za 3,0 min. Protizávaží má hmotnost pouze 950 kg, takže motor zdviže musí napomáhat k vyvažování kabiny. Jaký musí být průměrný výkon tažné síly motoru, který působí na kabinu prostřednictvím tažného lana?
Zápis
M = 1200 kg hmotnost kabiny m = 950 kg hmotnost protizávaží s = 54 m výška, do níž je potřeba zdvihnout kabinu t = 3 min doba na zdvihnutí kabiny P = ? průměrný výkon tažné síly motoru Rozbor
Budeme předpokládat, že se kabina zdviže pohybuje vzhůru rovnoměrně. Nejprve zjistíme, jak velká musí být tažná síla motoru. Pak spočítáme, jakou práci vykoná tažná síla motoru při zvednutí kabiny do dané výšky. Nakonec určíme hledaný výkon tažné síly motoru.
Nápověda 1 – působící síly
Nakreslete si obrázek a vyznačte do něho síly působící na kabinu.
Předpokládejte, že se kabina zdviže pohybuje vzhůru rovnoměrně. Co platí pro výslednou sílu, která na ni působí? Jak velkou silou musí táhnout motor?
Nápověda 2 – práce a výkon
Tažná síla motoru je konstantní. Jakou práci vykoná motor při zvednutí kabiny do dané výšky? Jaký je výkon motoru?
Číselný výpočet
Je dáno:
\[M\,=\,1\,200\, \mathrm{kg}\] \[m\,=\,950\, \mathrm{kg}\] \[s\,=\,54\, \mathrm{m}\] \[t\,=\,3\, \mathrm{min}\,=\,180\, \mathrm{s}\] \[P\,=\,?\]Z tabulek:
\[g\,=\,9{,}81\, \mathrm{m \cdot s^{-2}}\]
\[P\,=\,\frac {\left(M-m\right)gs}{t}\] \[P\,=\,\frac{\left(1\,200\,-\,950\right)\cdot 9{,}81{\cdot}54}{180}\,\mathrm{W}\] \[P\,=\,735{,}75\, \mathrm{W}\,\dot=\,736\ \mathrm{W}\]Odpověď
Průměrný výkon tažné síly motoru je \[P\,=\,\frac {\left(M-m\right)gs}{t}\,\dot=\,736\ \mathrm{W}.\]
Celkové řešení
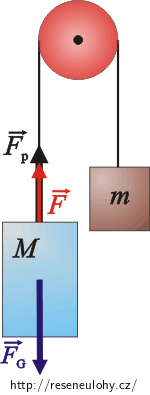
\(M\) … hmotnost kabiny
\(m\) … hmotnost protizávaží
\(\vec F_\mathrm{g}\) … tíhová síla působící na kabinu \((F_\mathrm{g}\,=\,Mg)\)
\(\vec F_\mathrm{p}\) … tažná síla protizávaží \((F_\mathrm{p}\,=\,mg)\)
\(\vec F\) … tažná síla motoru
Při rovnoměrném pohybu je zrychlení i výsledná síla působící na kabinu nulová. Platí tedy:
\[F_\mathrm{p}+F-F_\mathrm{g}\,=\,0\,.\]Tažná síla motoru bude rovna
\[F\,=\,Mg-mg\,.\tag{1}\]Práce tažné síly motoru:
Práci konstantní síly, která působí ve směru posunutí na dráze s, můžeme vyjádřit vztahem:
\[W\,=\,Fs\,.\]Za sílu F dosadíme ze vztahu (1):
\[W\,=\,\left(Mg-mg\right)s\,=\,\left(M-m\right)gs\,.\tag{2}\]Výkon tažné síly motoru:
Výkon vyjadřuje, jak rychle se koná práce:
\[P\,=\, \frac {W}{t}\,.\]Za práci dosadíme ze vztahu (2):
\[P\,=\,\frac {\left(M-m\right)gs}{t}\,,\] \[P\,=\,\frac{\left(1\,200\,-\,950\right)\cdot 9{,}81{\cdot}54}{180}\,\mathrm{W},\] \[P\,=\,735{,}75\, \mathrm{W}.\]Odpověď: Průměrný výkon tažné síly motoru je \(P\,=\,735{,}75\, \mathrm{W}.\)





