Nezodpovědný řidič
Úloha číslo: 103
Nákladní dodávka jede po přímé silnici stálou rychlostí 86 km·h−1. Po ujetí dráhy 10,4 km náhle dojde palivo. Řidič pokračuje pěšky v původním směru. Za 27 min dojde k čerpací stanici, vzdálené od odstavené dodávky 2,4 km. Jaká je průměrná rychlost vp řidiče od chvíle, kdy vyjel s dodávkou z výchozího místa, až do okamžiku příchodu k čerpací stanici?
Řešte výpočtem i graficky.
Poznámka: Průměrnou rychlost užíváme ve smyslu průměrné velikosti rychlosti.
Zápis
v = 86 km·h−1 rychlost dodávky x1 = 10,4 km dráha, kterou ujela dodávka xc = 2,4 km vzdálenost čerpací stanice od dodávky t2 = 27 min doba, za kterou došel řidič na čerpací stanici vp = ? (km·h−1) průměrná rychlost řidiče Nápověda 1: Početní řešení
Jak daleko je čerpací stanice od místa, z kterého dodávka vyjela, a jak dlouho jel řidič, než mu došel benzín? Jak dlouho řidiči trvalo (z místa vyjetí), než se k čerpací stanici dostal?
Jak spočítáte průměrnou rychlost, znáte-li celkovou dráhu a celkový čas?
Nápověda 2: Grafické řešení
Úlohu můžete řešit i graficky. Nakreslete si závislost x(t) pro oba úseky do jednoho grafu. Spojte koncový bod s počátkem. Jaký význam má směrnice této přímky? Jak ji určíte?
CELKOVÉ ŘEŠENÍ
Pro výpočet průměrné rychlosti vp musíme znát celkovou dráhu Δx a dobu Δt . Je výhodné položit počátek souřadnicové osy x do místa, odkud automobil vyrazil (tedy x0 = 0 km), a orientovat osu tak, aby směr jízdy byl kladný.
Poloha čerpací stanice na takto zvolené ose je:
\[x_2\,=\,x_1+x_c\,.\]A tedy:
\[\Delta{x}\,=\,x_2-x_0\,=\,x_2\,=\,x_1+x_c\,.\]Dobu jízdy určíme z rovnice:
\[t_1\,=\,\frac{x_1-x_0}{v}\,=\,\frac{x_1}{v}\,.\]Celková doba cesty řidiče (jízda i chůze) je:
\[\Delta{t}\,=\,t_1+t_2\,=\,\frac{x_1}{v}+t_2\,,\]kde:
t1…je doba jízdy,
t2…je doba chůze.
Dosadíme do vzorce pro výpočet průměrné rychlosti:
\[v_\mathrm{p}\,=\,\frac{\Delta{x}}{\Delta{t}}\,=\,\frac{x_1+x_c}{\frac{x_1}{v}+t_2}\,.\]Číselně (převedeme t2 = 27 min = 0,45 h):
\[v_\mathrm{p}\,=\,\frac{(10{,}4+2{,}4)\,\mathrm{km}}{(\frac{10{,}4}{86}+0{,}45)\,\mathrm{h}}\,=\,22\,\mathrm{km.h^{-1}}\,.\]Grafické řešení:
Průměrnou rychlost vp zjistíme také graficky.
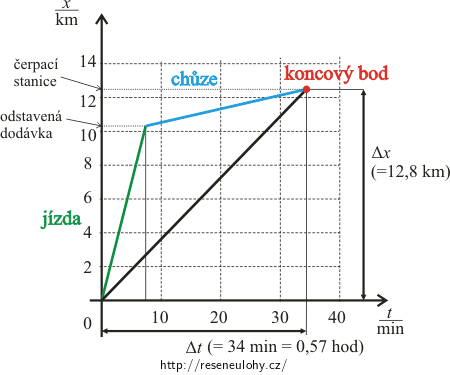
Nejprve narýsujeme graf funkce x(t) (viz obrázek). Výchozí bod splývá s počátkem.
Průměrná rychlost je směrnicí přímky spojující výchozí bod a koncový bod. Z délek úseček Δt a Δx je zřejmé, že směrnice má hodnotu:
\[v_\mathrm{p}\,=\,\frac{(12{,}8)\,\mathrm{km}}{(0{,}57)\,\mathrm{h}}\,\dot=\,22\,\mathrm{km\cdot h^{-1}}\,.\]Odpověď
Průměrná rychlost vp řidiče od chvíle, kdy vyjel s dodávkou z výchozího místa, až do okamžiku příchodu k čerpací stanici je:
\[v_\mathrm{p}\,=\,\frac{\mathrm{\Delta}x}{\mathrm{\Delta}t}\,=\,\frac{x_1+x_c}{\frac{x_1}{v}+t_2}\,.\]Číselně (převedeme t2 = 27 min = 0,45 h):
\[v_\mathrm{p}\,\dot=\,22\,\mathrm{km\cdot h^{-1}}\,.\]Grafické řešení:
Průměrná rychlost je směrnicí přímky spojující výchozí bod a koncový bod:
\[v_\mathrm{p}\,=\,\frac{(12{,}8)\,\mathrm{km}}{(0{,}57)\,\mathrm{h}}\,\dot=\,22\,\mathrm{km\cdot h^{-1}}\,.\]