Záchranný letoun

Úloha číslo: 130

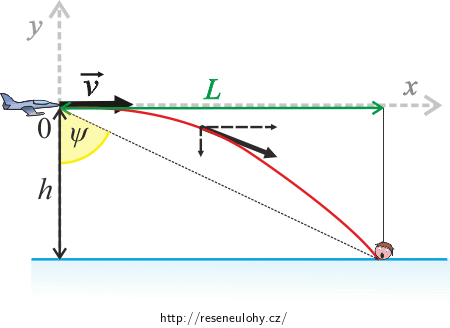
Záchranný letoun letí na pomoc tonoucímu. Pilot udržuje stálou výšku 1 200 m nad hladinou a směřuje přímo nad hlavu člověka (viz obrázek). Rychlost letadla má velikost 430 km·h⁻¹.

Při jakém zorném úhlu musí pilot uvolnit záchranný vak, aby dopadl co nejblíže k tonoucímu?

Odpor prostředí neuvažujte.

Zápis

h = 1 200 m výška letadla nad hladinou

v = 430 km·h⁻¹ rychlost letadla

ψ = ? (°) zorný úhel

Z tabulek:

g = 9,81 m·s⁻² tíhové zrychlení
Nápověda 1: Počáteční rychlost vaku
Jaká je počáteční rychlost vaku? Znáte její velikost?
Řešení k nápovědě 1
Počáteční rychlost vaku je shodná s rychlostí letadla. Má tedy velikost v.
Nápověda 2: Doba pádu vaku na hladinu
Jakým pohybem se vak po vypuštění pohybuje ve svislém směru?

Jak zjistíte dobu jeho pádu t na hladinu, víte-li, v jak velké výšce h nad hladinou byl vypuštěn?
Řešení k nápovědě 2
Neuvažujeme-li odpor prostředí, pohybuje se vak ve svislém směru volným pádem.

Protože víme, v jak velké výšce je vak vypuštěn, můžeme snadno určit dobu jeho pádu na hladinu. Ve směru osy y platí:
\[-h\,=\,-\,\frac{1}{2}gt^{2}\,,\]
tedy:
\[h\,=\,\frac{1}{2}gt^{2}\,\]
(ve směru osy y na vak působí jen tíhová síla).

Řešením této rovnice dostáváme pro dobu letu t:
\[t\,=\,\sqrt{\frac{2h}{g}}\,.\]
Nápověda 3: Vzdálenost L
Jak se vak pohybuje ve vodorovném směru?

Jak velkou vzdálenost L ve vodorovném směru urazí vak za dobu t, tedy za dobu pádu na hladinu? Dobu pádu t znáte z předchozí nápovědy.
Řešení k nápovědě 3
Ve vodorovném směru se vak (i letadlo) pohybuje stálou rychlostí v.

Z předchozí nápovědy si připomeneme, co platí pro dobu t pádu vaku na hladinu:
\[t\,=\,\sqrt{\frac{2h}{g}}\,.\]
Za tuto dobu urazí vak ve vodorovném směru vzdálenost:
\[L\,=\,vt\,.\]
Po dosazení za t dostáváme:
\[L\,=\,v\,\sqrt{\frac{2h}{g}}\,.\]
Nápověda 4: Zorný úhel ψ
Jak zjistíte velikost zorného úhlu ψ, při kterém musí pilot uvolnit záchranný vak, aby dopadl co nejblíže k tonoucímu?

Podívejte se na obrázek. Jakou goniometrickou funkci k výpočtu použijete?

Které veličiny k vyjádření zorného úhlu ψ potřebujete? Znáte je?
Řešení k nápovědě 4
Výpočet zorného úhlu ψ je zřejmý z obrázku.

Použijeme goniometrickou funkci tangens.

K výpočtu potřebujeme znát vzdálenost L, kterou ve vodorovném směru urazí vak za dobu t svého pádu na hladinu, a výšku, ze které padá. Obojí již známe.

Platí:
\[\mathrm{tg}\psi\,=\,\frac{L}{h}\,=\,\frac{v\,\sqrt{\frac{2h}{g}}}{h}\,=\,v\,\sqrt{\frac{2}{hg}}\,.\]
Číselně:
\[\mathrm{tg}\psi\,=\frac{430\, 000}{3\, 600}\sqrt{\frac{2}{1\, 200{\cdot}9{,}81}}\,\dot=\, 1{,}556\,,\] \[\psi\,=\,57^{\circ}\,.\]

Poznámka: Vodorovný průmět rychlosti vaku je v každém okamžiku shodný s rychlostí letadla, takže pilot vidí letící vak neustále pod sebou.
CELKOVÉ ŘEŠENÍ:
Počáteční rychlost vaku je shodná s rychlostí letadla. Má tedy velikost \(v\).

Neuvažujeme-li odpor prostředí, pohybuje se vak ve svislém směru volným pádem.

Protože víme, v jak velké výšce je vak vypuštěn, můžeme snadno určit dobu jeho pádu na hladinu. Ve směru osy y platí:
\[-h\,=\,-\,\frac{1}{2}gt^{2}\,,\]
tedy:
\[h\,=\,\frac{1}{2}gt^{2}\,\]
(ve směru osy y na vak působí jen tíhová síla).

Řešením této rovnice dostáváme pro dobu letu t:
\[t\,=\,\sqrt{\frac{2h}{g}}\,.\]

Ve vodorovném směru se vak (i letadlo) pohybuje stálou rychlostí v.

Za tuto dobu urazí vak ve vodorovném směru vzdálenost:
\[L\,=\,vt\,.\]
Po dosazení za t dostáváme:
\[L\,=\,v\sqrt{\frac{2h}{g}}\,.\]

Výpočet zorného úhlu ψ je zřejmý z obrázku.

Použijeme goniometrickou funkci tangens.

K výpočtu potřebujeme znát vzdálenost L, kterou ve vodorovném směru urazí vak za dobu t svého pádu na hladinu, a výšku, ze které padá. Obojí již známe.

Platí:
\[\mathrm{tg}\psi\,=\,\frac{L}{h}=\frac{v\sqrt{\frac{2h}{g}}}{h}=v\sqrt{\frac{2}{hg}}\,.\]

Číselně:
\[\mathrm{tg}\psi\,=\,\frac{430 \,000}{3\, 600}\sqrt{\frac{2}{1 \,200{\cdot}9{,}81}}\,\dot=\, 1{,}556\,,\] \[\psi\,=\,57^{\circ}\,.\]

Poznámka: Vodorovný průmět rychlosti vaku je v každém okamžiku shodný s rychlostí letadla, takže pilot vidí letící vak neustále pod sebou.
Odpověď
Pilot musí uvolnit záchranný vak, aby dopadl co nejblíže k tonoucímu, v zorném úhlu ψ, pro který platí:
\[\mathrm{tg}\psi\,=\,v\,\sqrt{\frac{2}{hg}}\,\dot=\,1{,}556\,,\] \[\psi\,=\,57^{\circ}\,.\]